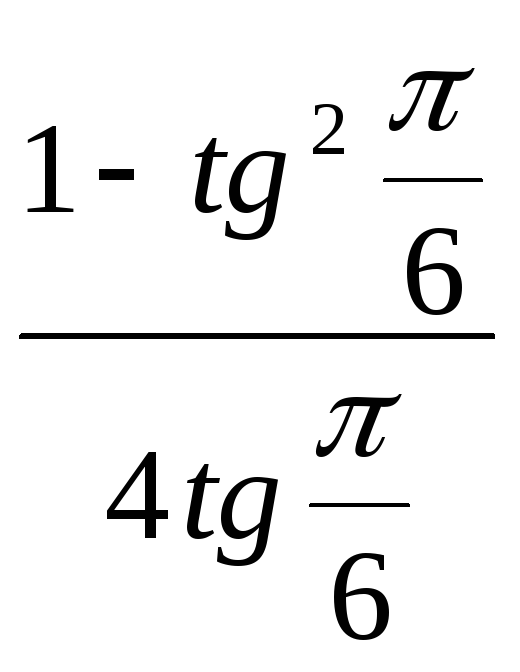- •2. Розділ 2 границі функції в точці та
- •5. Розділ 5. Похідна функції та її
- •Приклади для розв’язування.................................................44
- •6..4 Приклади для розв’язування........................................................54
- •Приклади для розв’язування.................................................64
- •Приклади для розв’язування......................................................73
- •Розділ 1. Функції, їх властивості та графіки План
- •Приклади для розв’язування.
- •Елементарні функції та їх графіки
- •4. Найпростіші перетворення графіків функцій.
- •5. Приклади для розв’язування.
- •3. Побудувати графік функції та указати область значень:
- •Розділ 2. Границі функції в точці та на нескінченності та їх використання для дослідження функцій План
- •Границя функції в точці.
- •Дослідження функції на неперервність
- •1. Границя функції в точці
- •2. Теореми про границі.
- •3. Правила обчислення границь.
- •4. Границя функції на нескінченності.
- •5.Дослідження функції на неперервність.
- •5. Приклади для розв’язування.
- •Розділ 3. Тригонометрія План
- •6. Основні формули тригонометрії.
- •7. . Найпростіші тригонометричні рівняння
- •8. Приклади для розв’язування.
- •1. Визначення тригонометричних функцій
- •Слід пам’ятати:
- •7. «Найпростіші тригонометричні рівняння»
- •8. Приклади для розв’язування.
- •Розділ 4. Степені та логарифми План
- •Приклади для розв’язування.
- •1. Степені. Корінь n-го степеня.
- •4. Поняття логарифмів .
- •6. Приклади для розв’язування
- •Розділ 5. Похідна та її використання План
- •Приклади для розв’язування
- •1. Поняття похідної функції.
- •2. Фізичний зміст похідної:
- •3. Геометричний зміст похідної.
- •4. Рівняння дотичної і нормалі до плоскої кривої.
- •Приклади для розв’язування
- •15. Знайти рівняння дотичної до графіка функції , яка паралельна прямій .
- •21. ***Задачі на знаходження найбільших та найменших значень величин.
- •Розділ 6. Інтеграл та його використання План
- •3. Таблиця невизначених інтегралів.
- •4. Визначений інтеграл.
- •1. Первісна та невизначений інтеграл.
- •2. Основні властивості невизначеного інтеграла.
- •3. Таблиця невизначених інтегралів.
- •Визначений інтеграл
- •6.Формула Ньютона – лейбніца.
- •7. Використання інтегралів для обчислення площі плоских фігур
- •Приклади для розв’язування.
- •6. Обчислити визначений інтеграл.
- •Розділ 7. Вектори та координати План
- •Вектори та дії з ними.
- •Лінійні операції над векторами.
- •Рівняння прямої на площині».
- •Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •1. Вектори та дії з ними.
- •2. Лінійні операції над векторами.
- •3. Рівняння прямої на площині».
- •4. Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •Розділ 8. . Стереометрія План
- •Приклади для розв’язування
- •Основні поняття стереометрії
- •2. Аксіоми стереометрії
- •3. Теореми стереометрії
- •4. Площі геометричних фігур.
- •5. Площі поверхонь та об’єми геометричних тіл.
- •6. Паралельні проекції деяких плоских фігур.
- •7.Приклади для розв’язування
Слід пам’ятати:
sin ( - α) = - sin α arcsin ( - α) = - arcsin α
cos ( - α) = cos α arccos ( - α) = π - arccos α
tg ( - α) = - tg α arctg ( - α) = - arctg α
ctg ( - α) = - ctg α arcctg ( - α) = π - arcctg α
sin ( α +2πk) = sin α
cos ( α +2πk) = cos α
tg ( α +πk) = tg α
ctg ( α +πk) = ctg α
. Основні формули тригонометрії.
І. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ СУМИ ДВОХ АРГУМЕНТІВ ( ФОРМУЛИ ДОДАВАННЯ
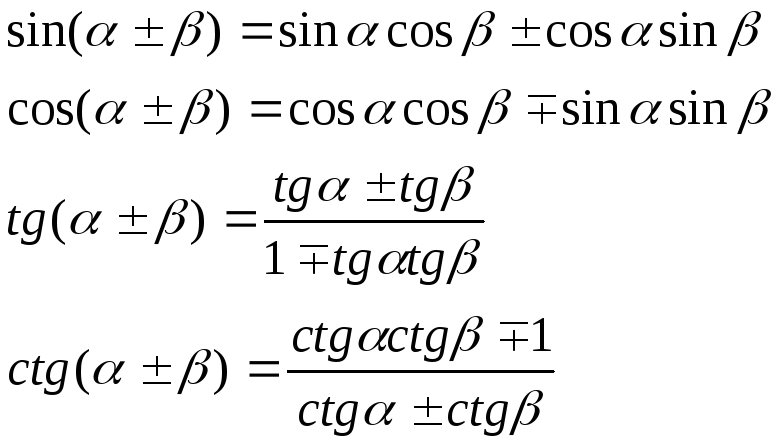
ІІ. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОДВОЄНОГО АРГУМЕНТА.
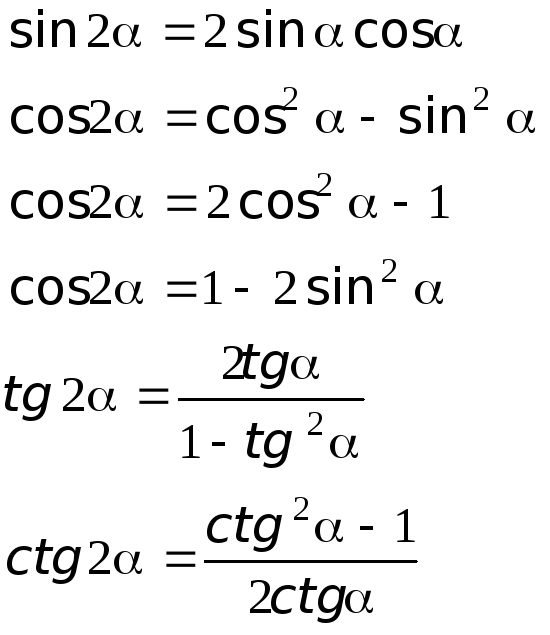
ІІІ. ФОРМУЛИ ЗНИЖЕННЯ СТЕПЕНІ.
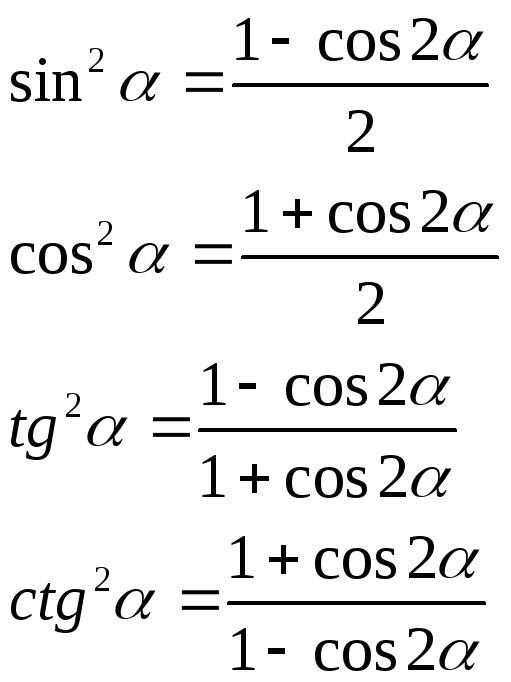
ІV/. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОЛОВИННОГО АРГУМЕНТА.
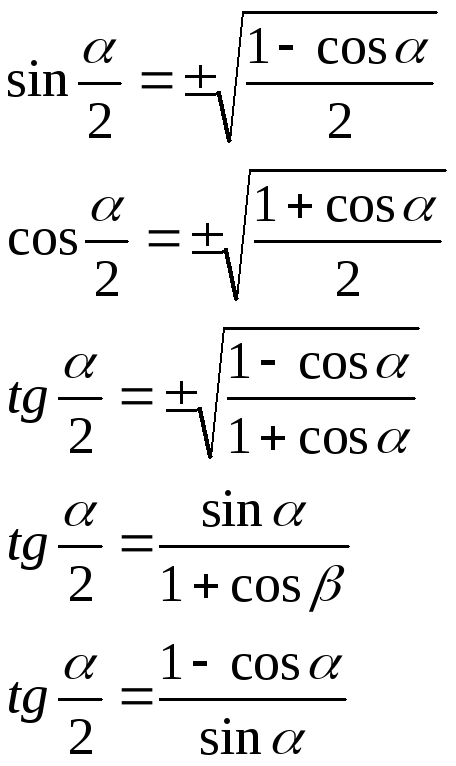
V. ПЕРЕТВОРЕННЯ ДОБУТКУ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА СУМУ.
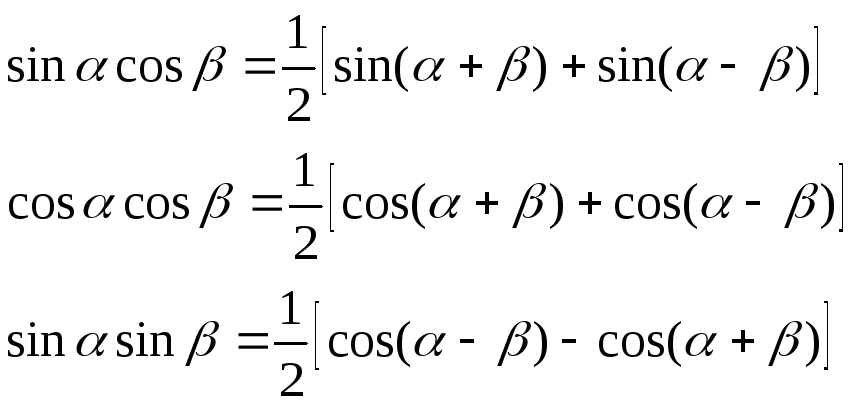
VI. ПЕРЕТВОРЕННЯ СУМИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА ДОБУТОК.
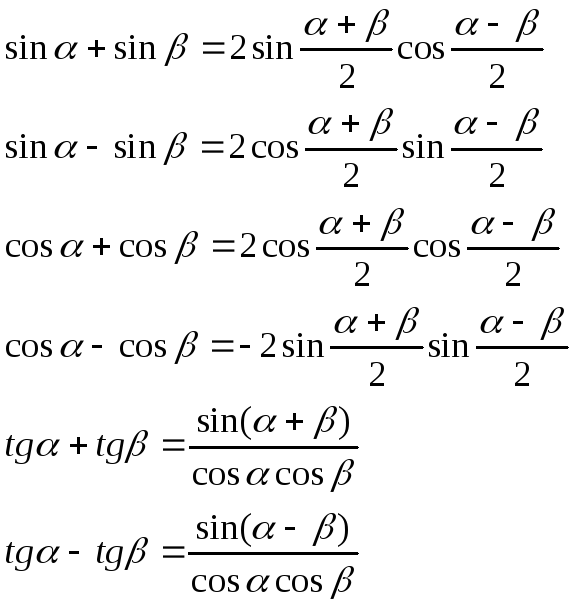
![]()
7. «Найпростіші тригонометричні рівняння»
-
№ п/п
Вид рівняння
Розв’язки
Приклад
1
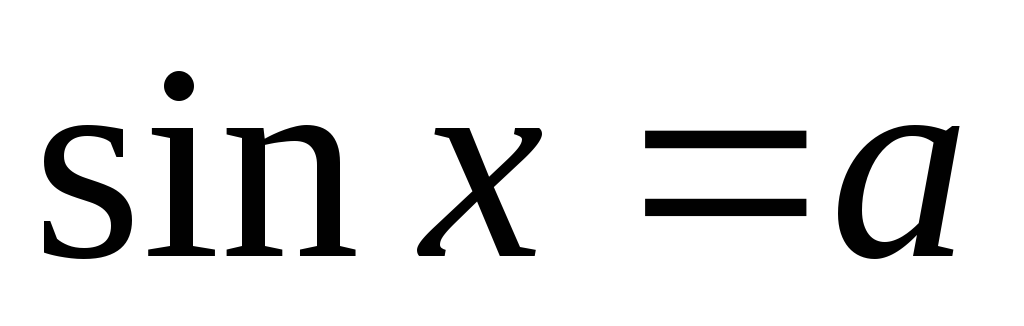
Якщо
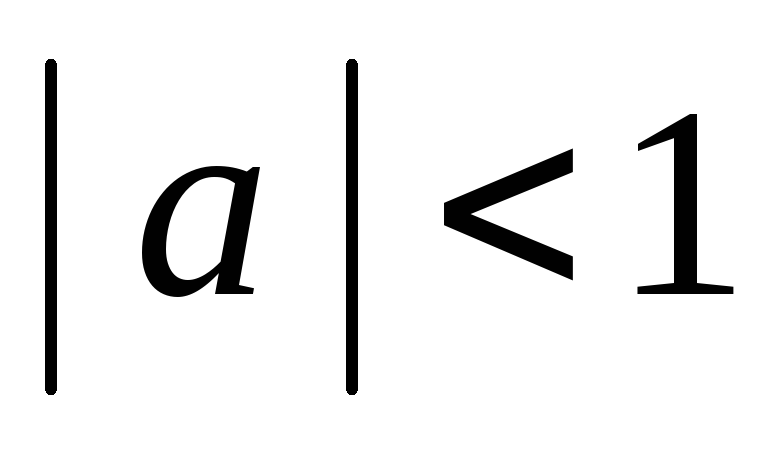 ,
то
,
то
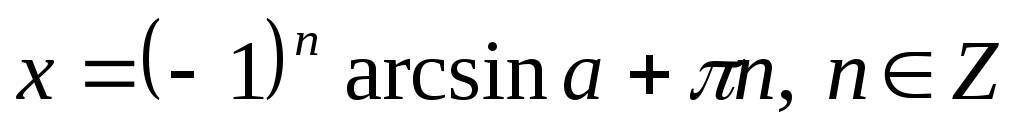
Якщо
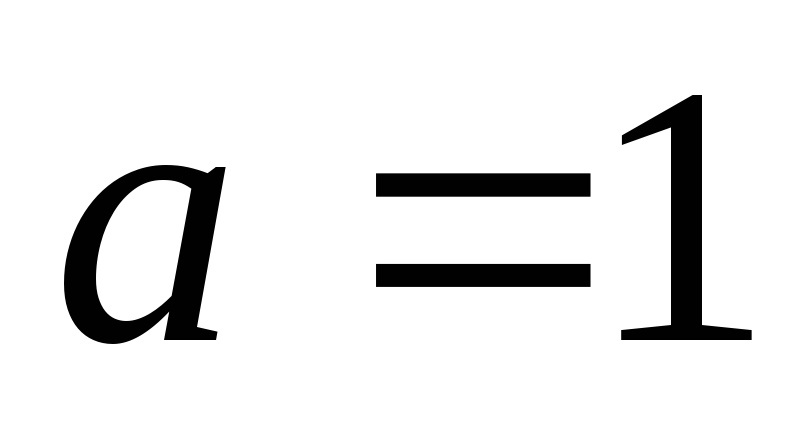 ,
то
,
то
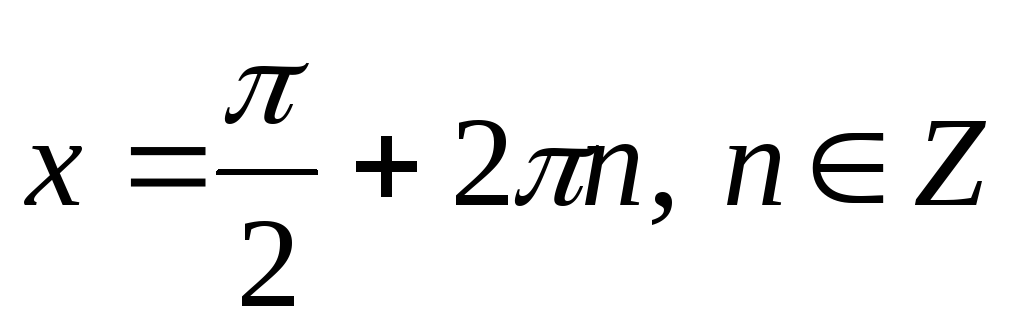
Якщо
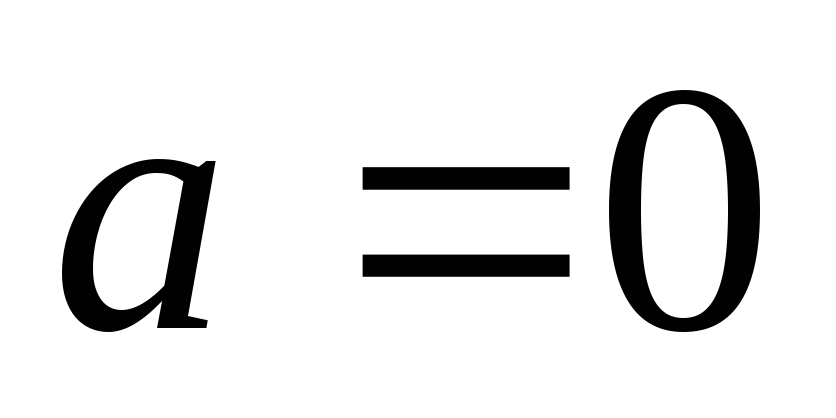 ,
то
,
то
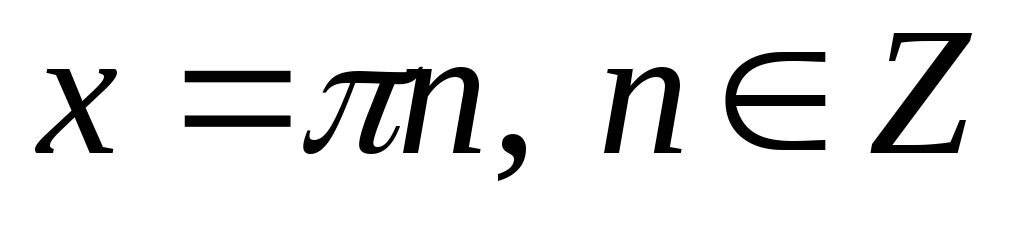
Якщо
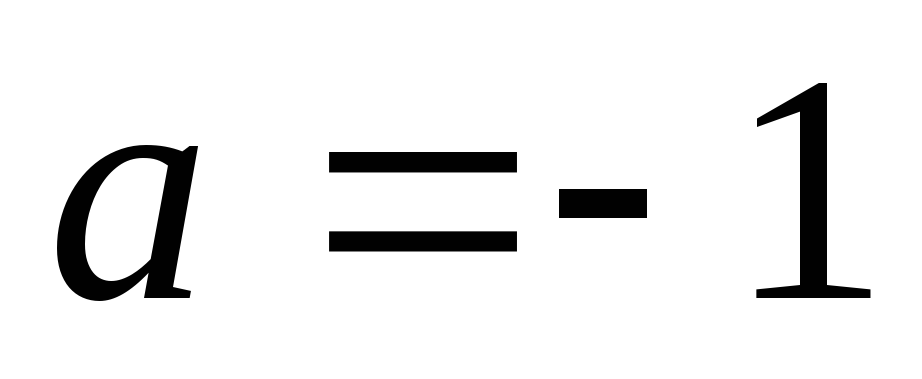 ,
то
,
то
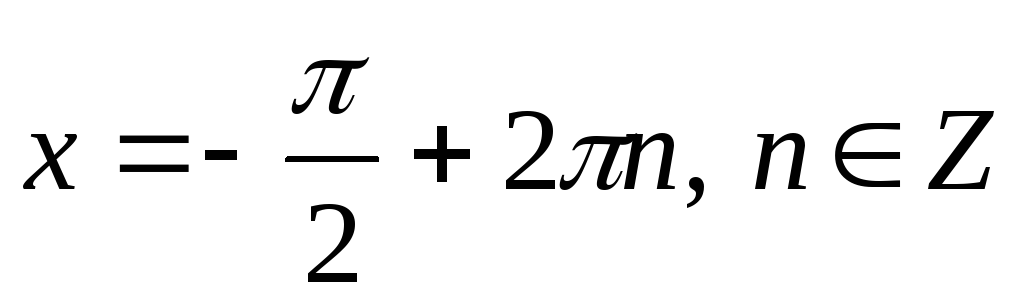
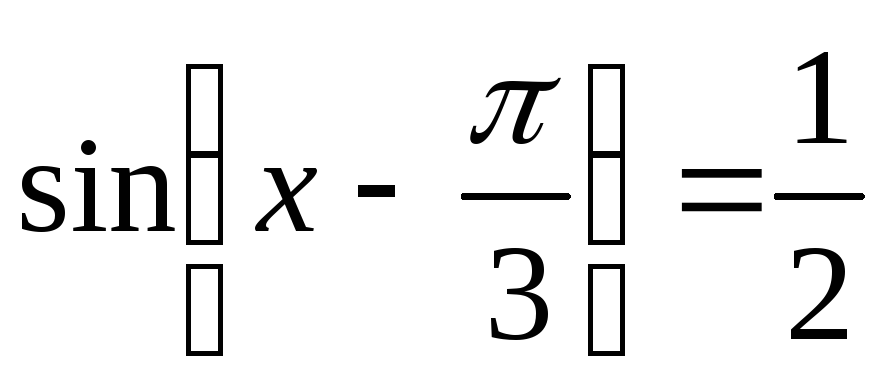

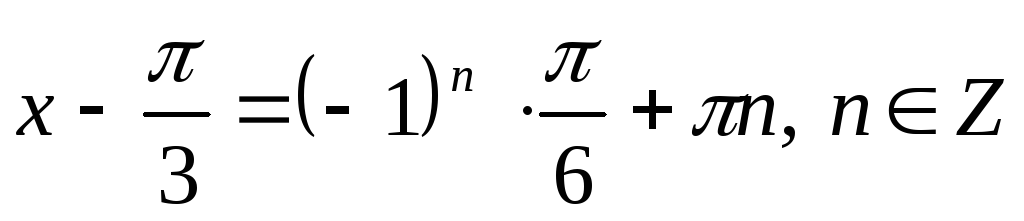
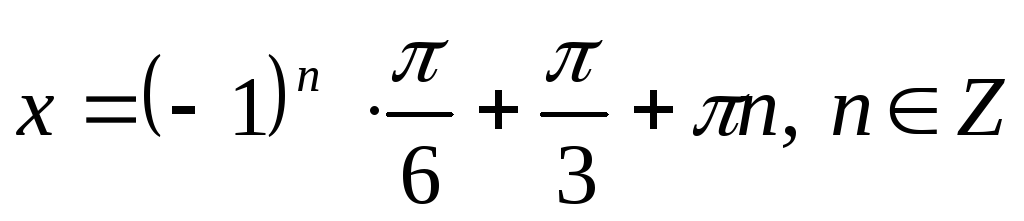
2.
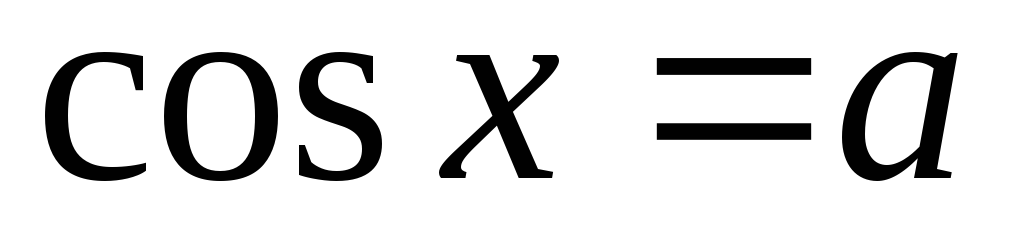
Якщо
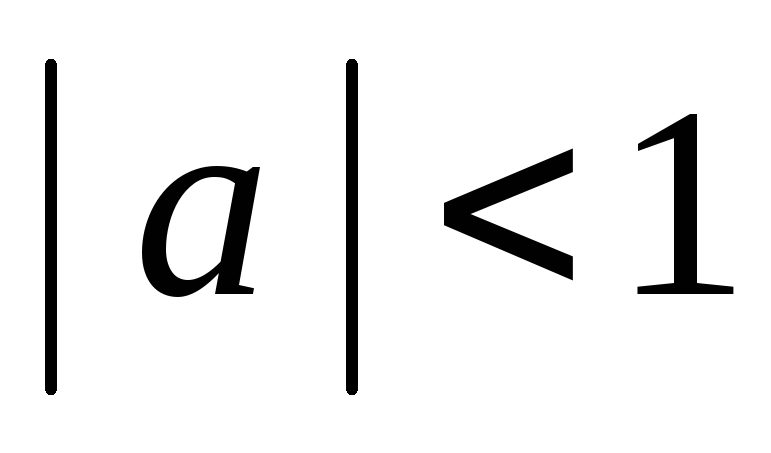 ,
то
,
то
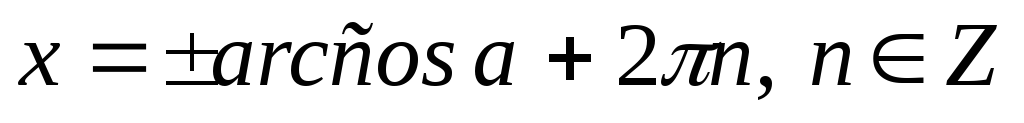
Якщо
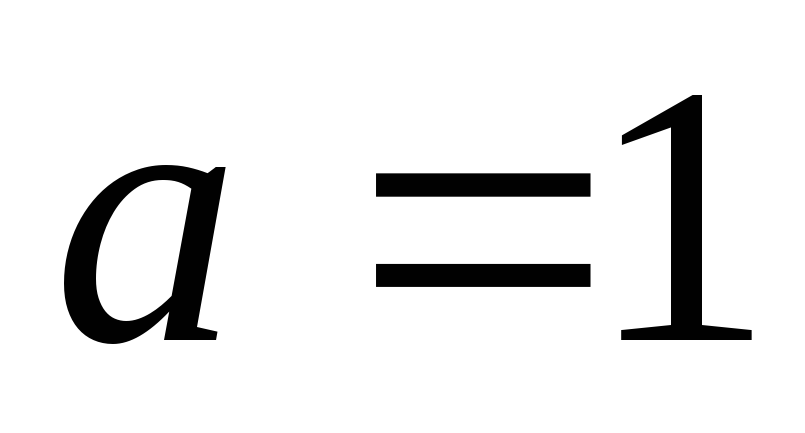 ,
то
,
то
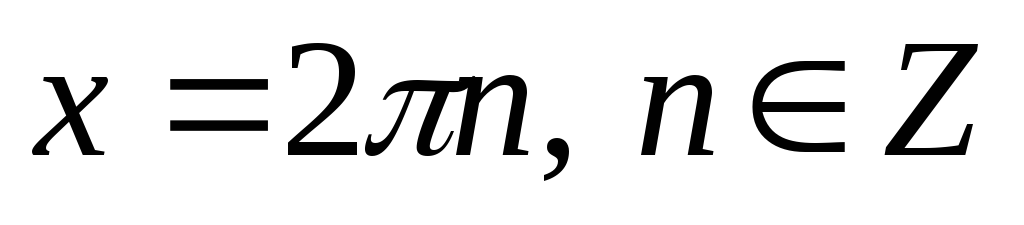
Якщо
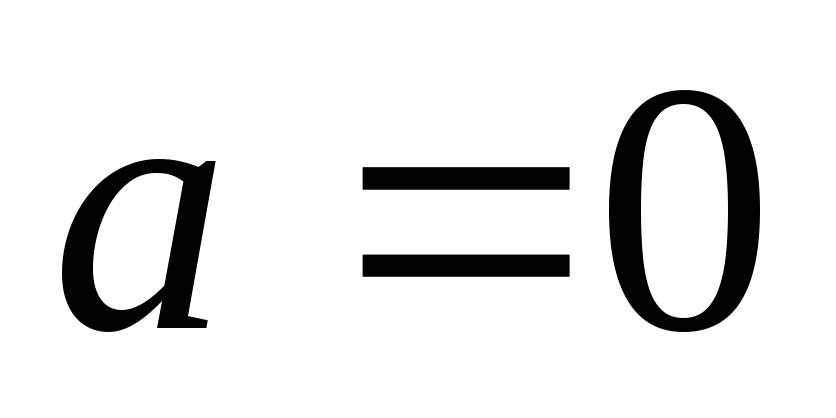 ,
то
,
то
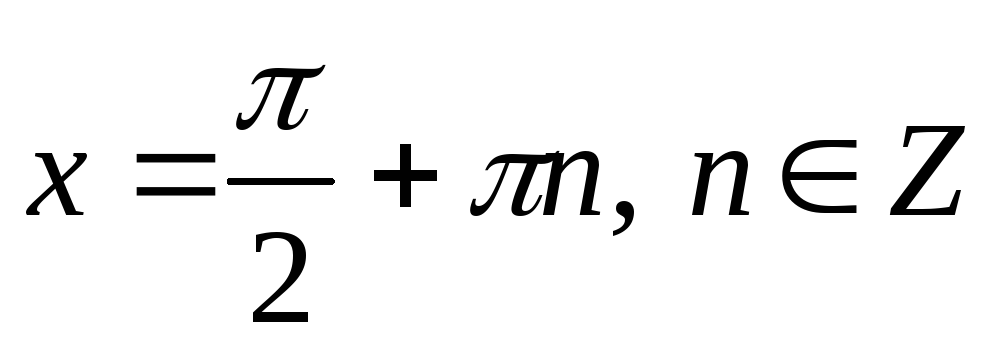
Якщо
 ,
то
,
то
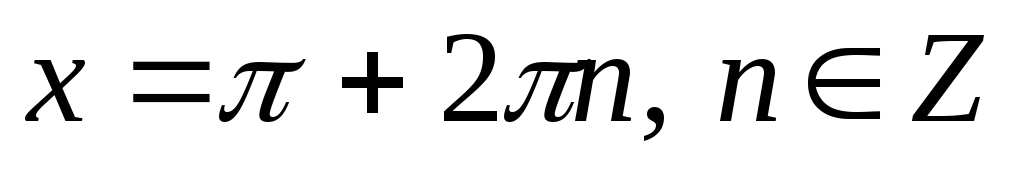
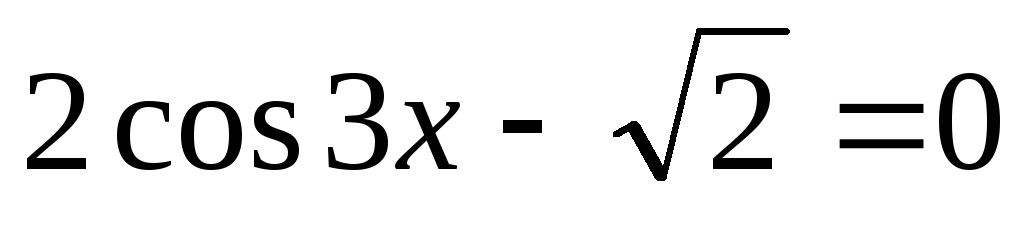
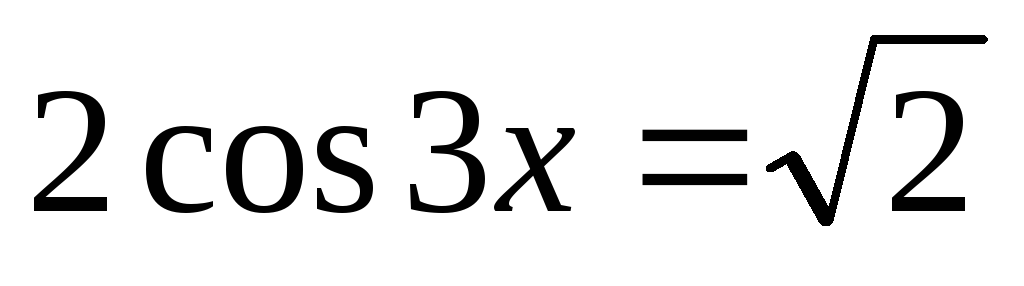
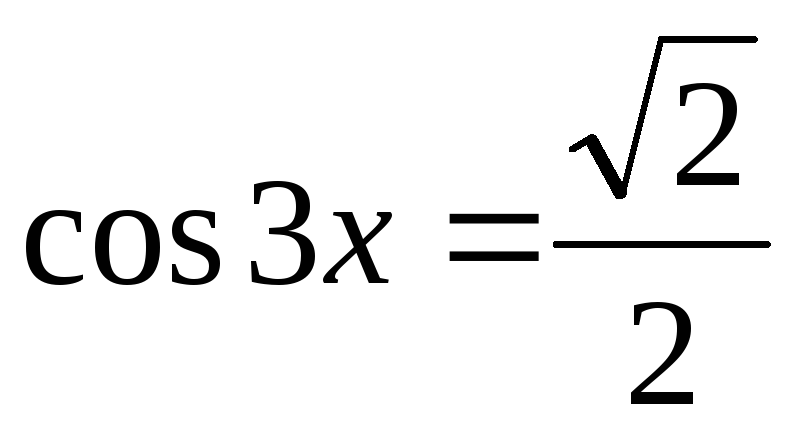
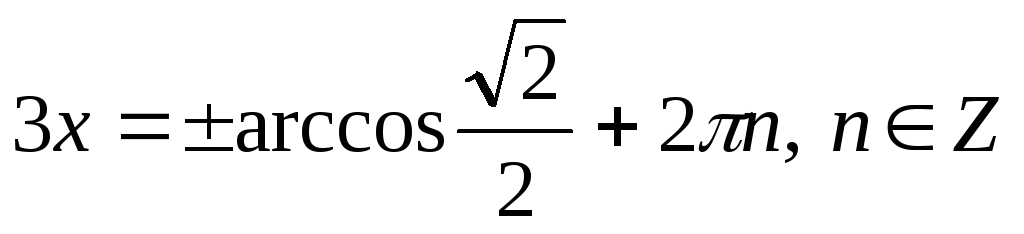
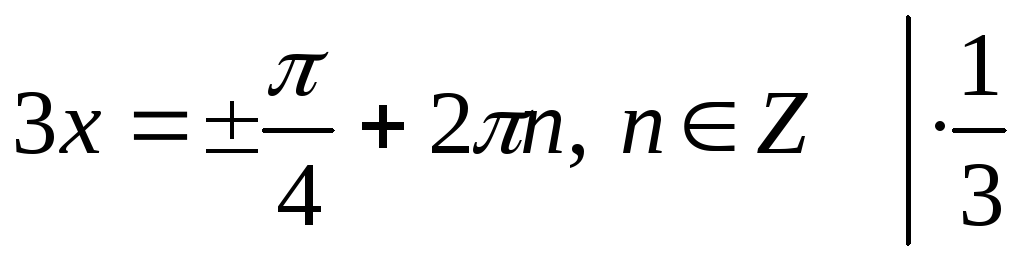
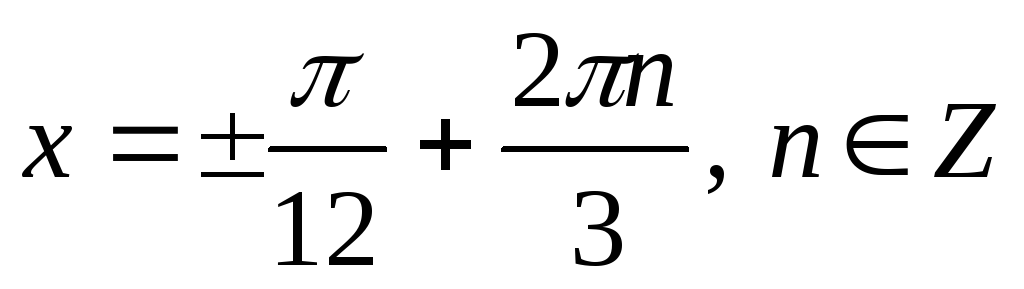
3.
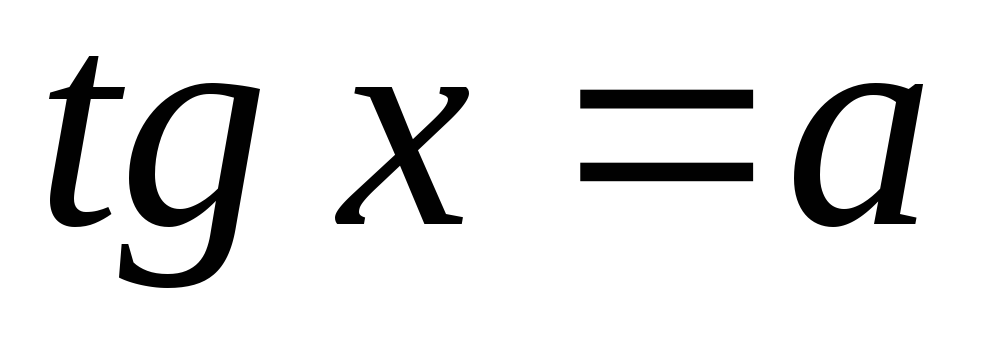
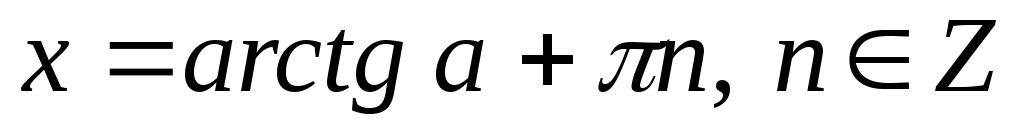
Якщо
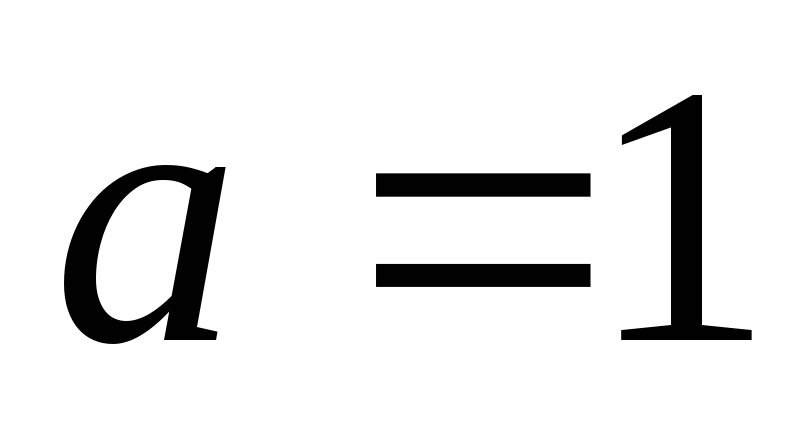 ,
то
,
то
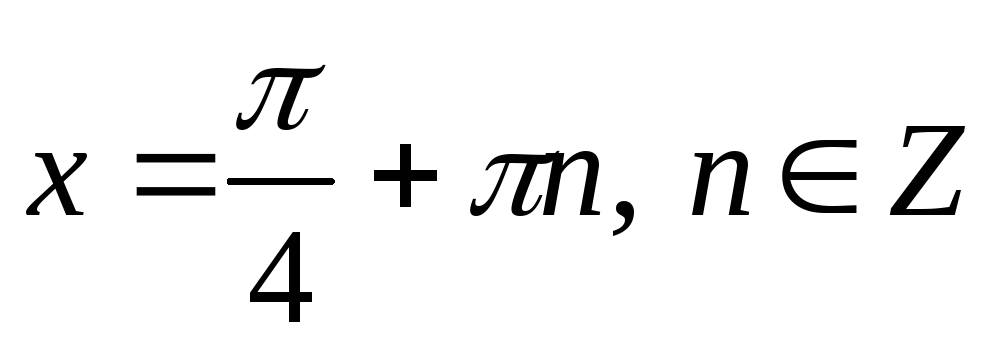
Якщо
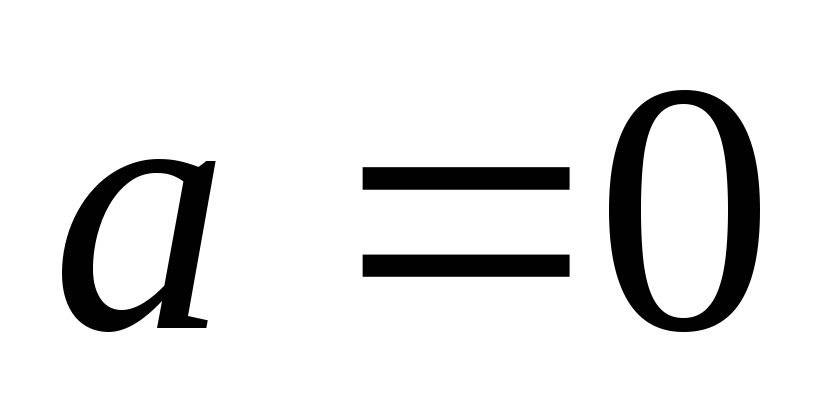 ,
то
,
то
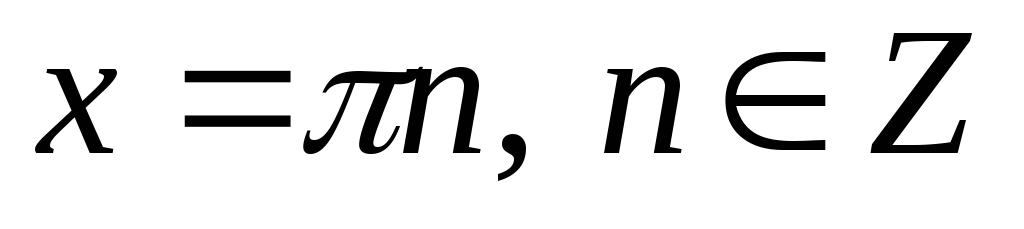
Якщо
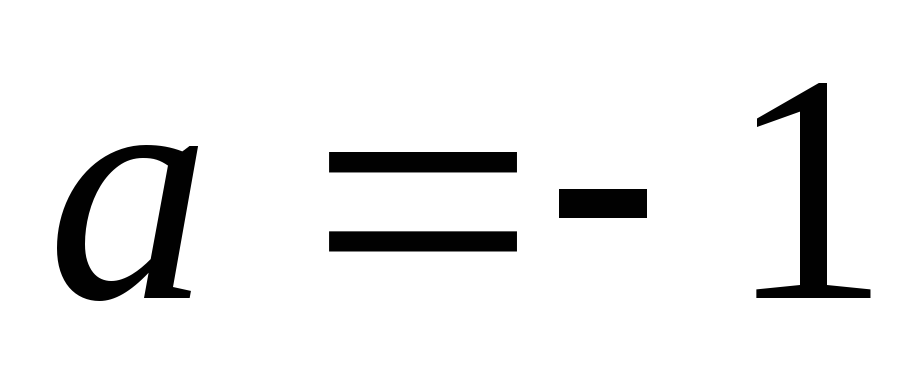 ,
то
,
то
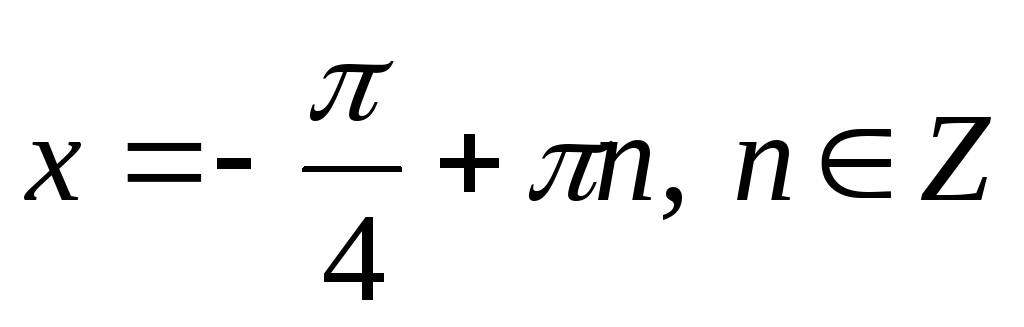
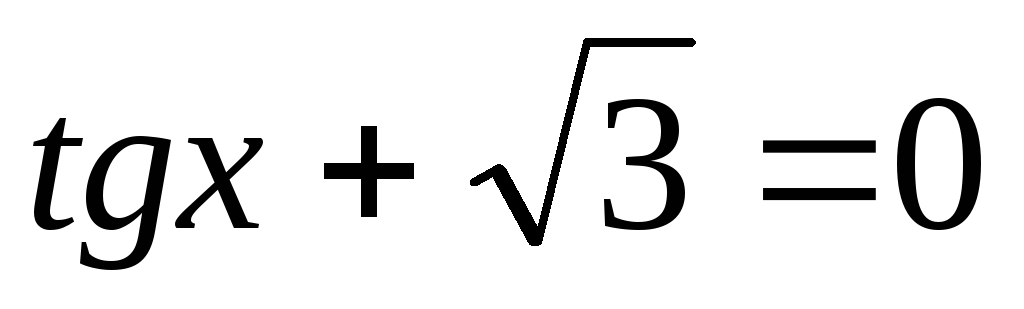
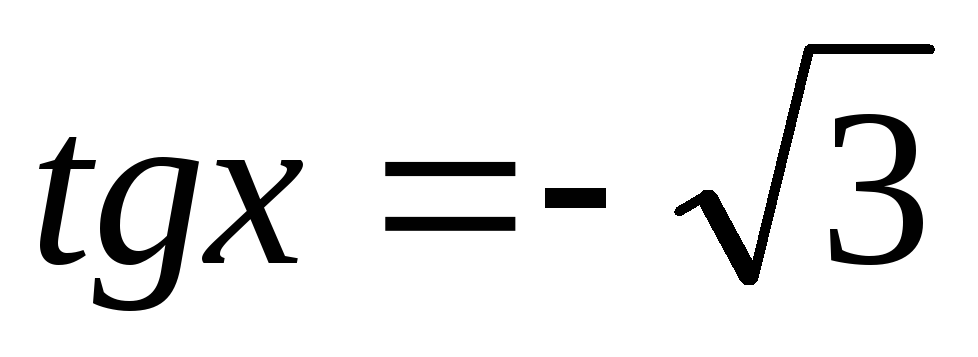
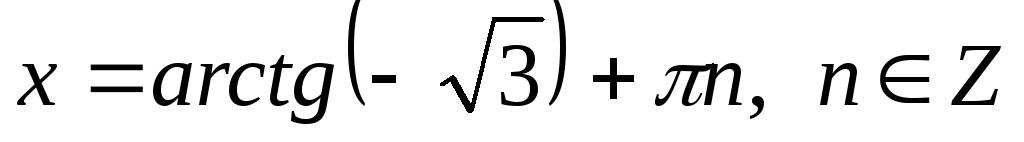
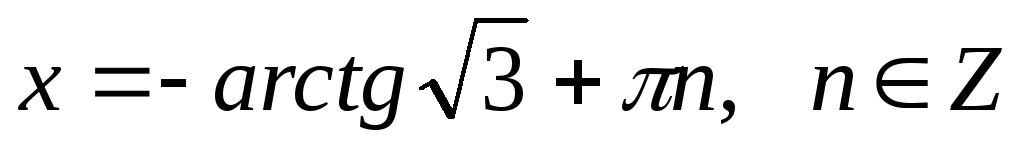
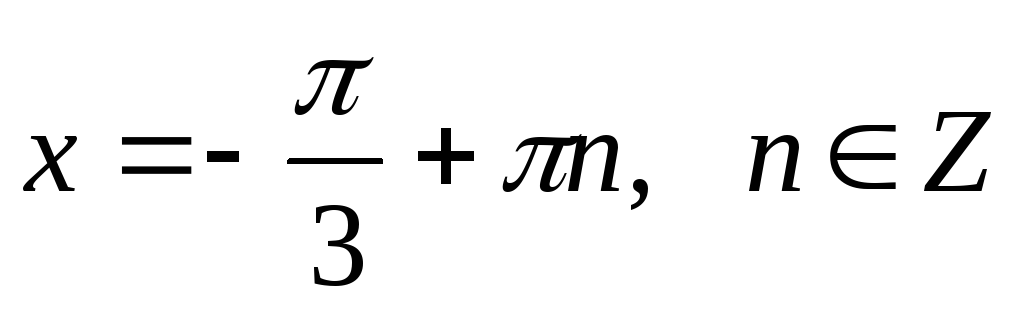
4.
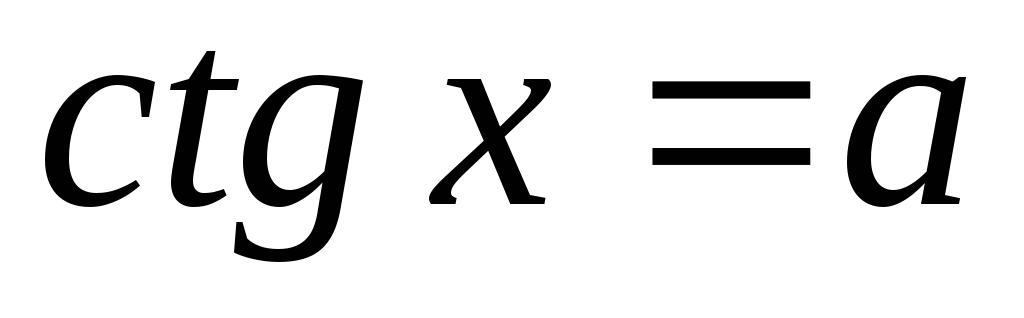
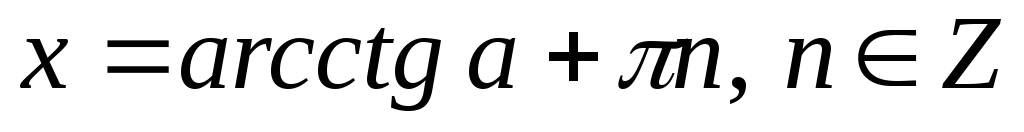
Якщо
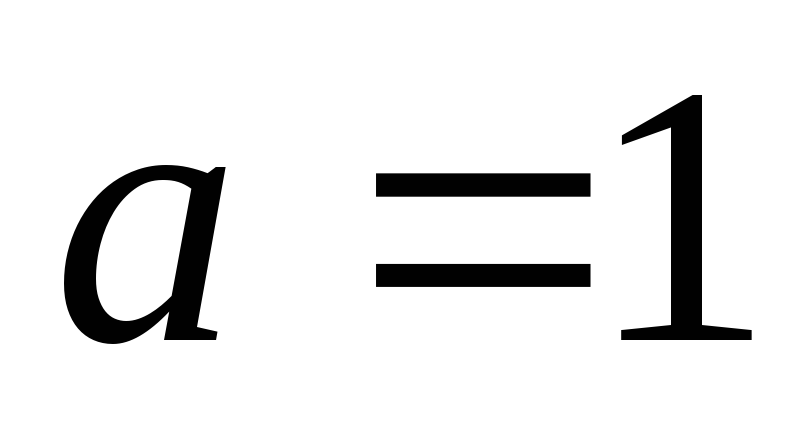 ,
то
,
то
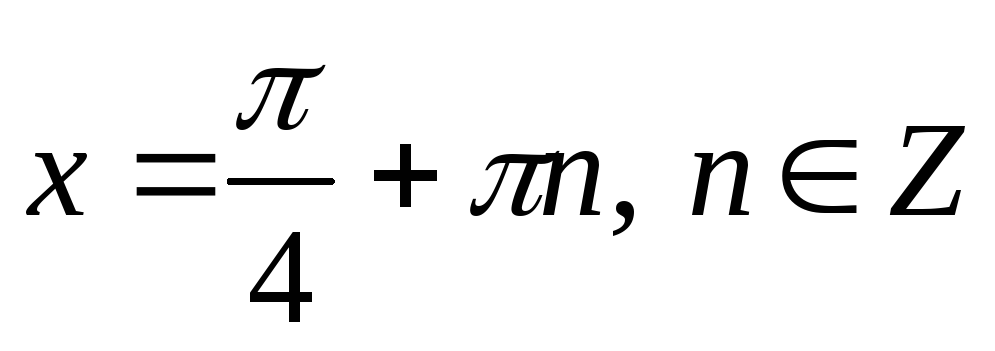
Якщо
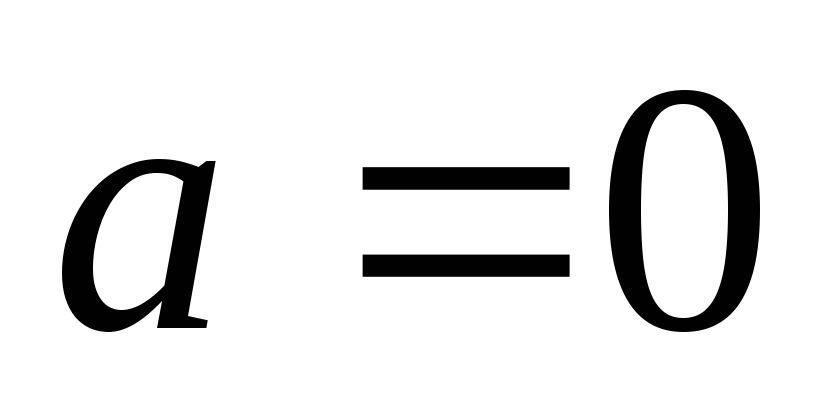 ,
то
,
то
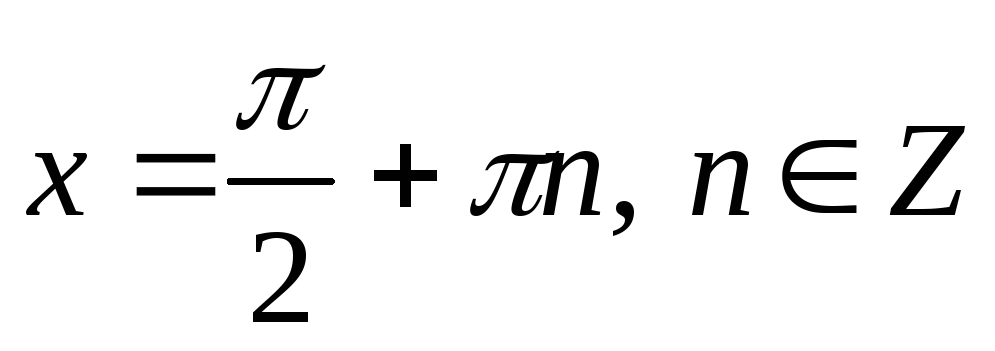
Якщо
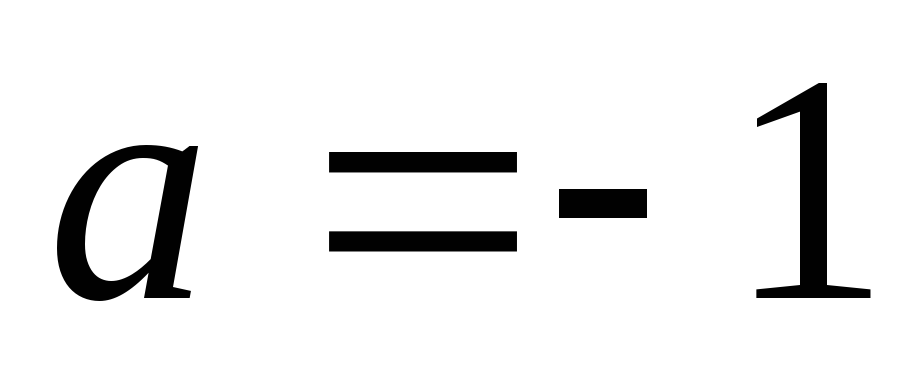 ,
то
,
то
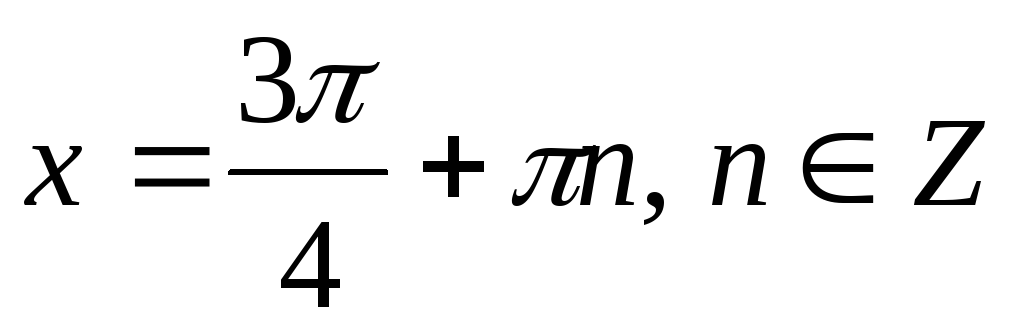
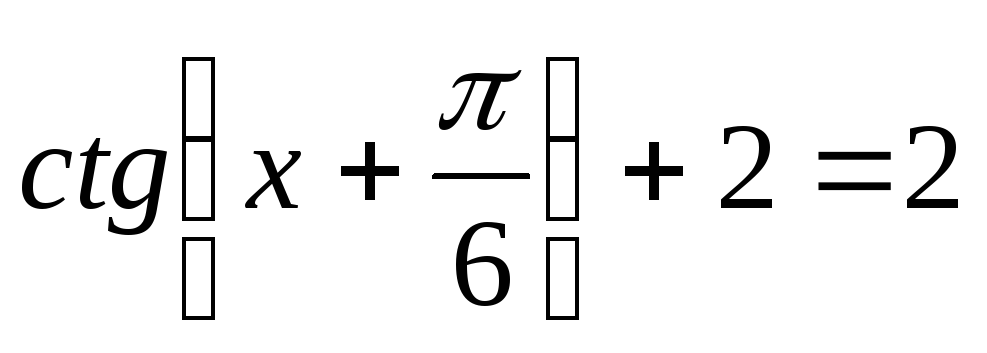
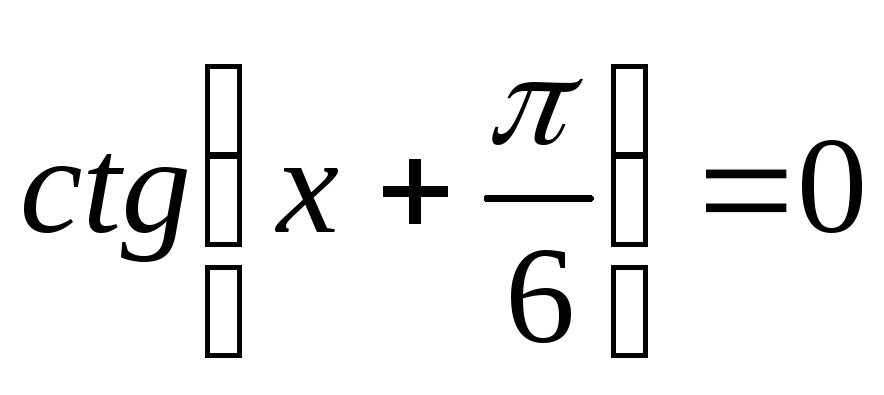
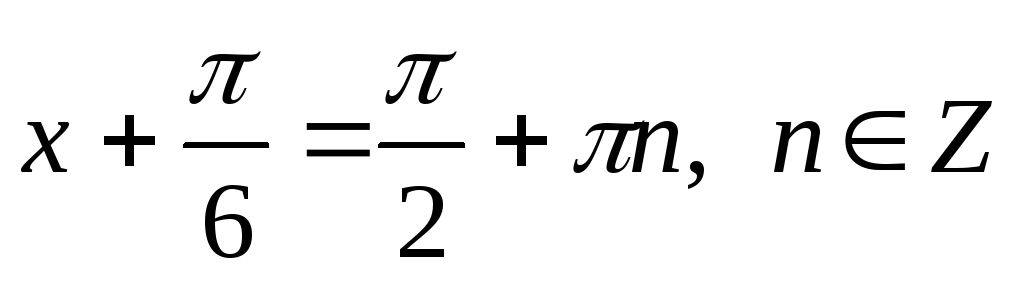
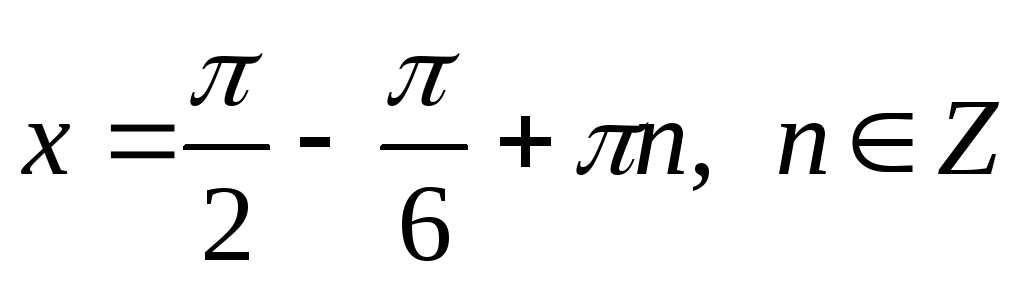
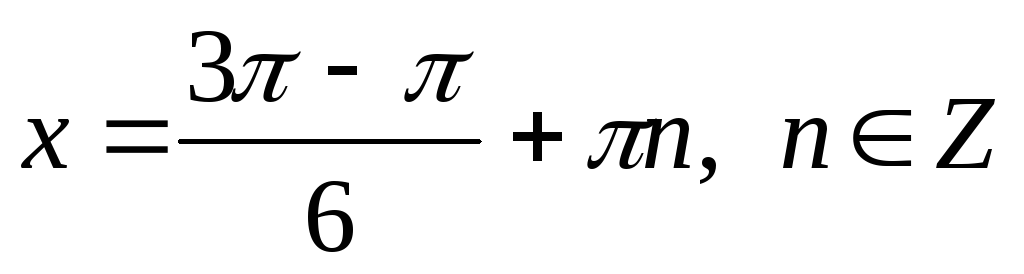
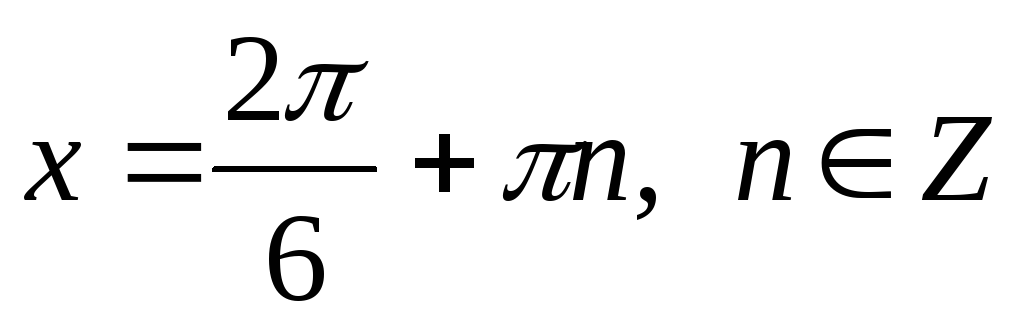
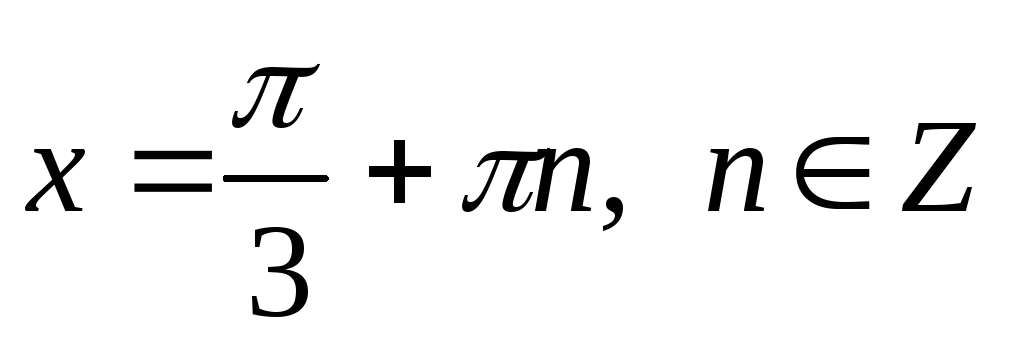
8. Приклади для розв’язування.
-
Виразити дані тригонометричні функції через функції аргумента, що вдвічі менші від даного.
-
*Дано:
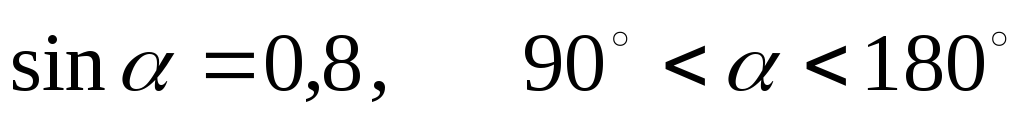
Знайти:
![]()
-
**Довести, що
-
Спростити.
-
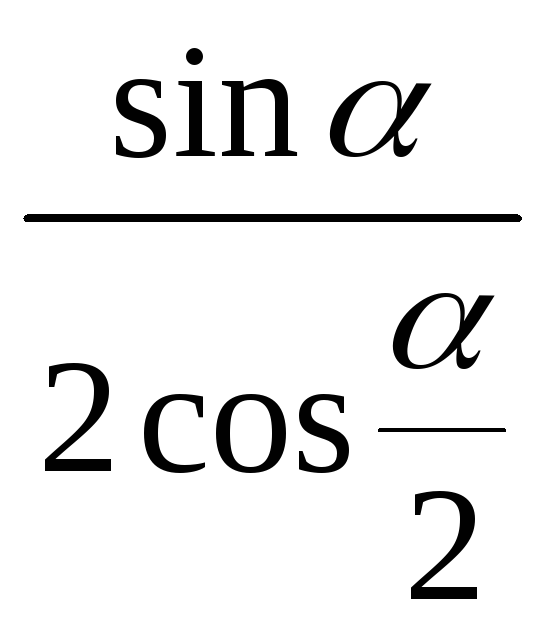
-
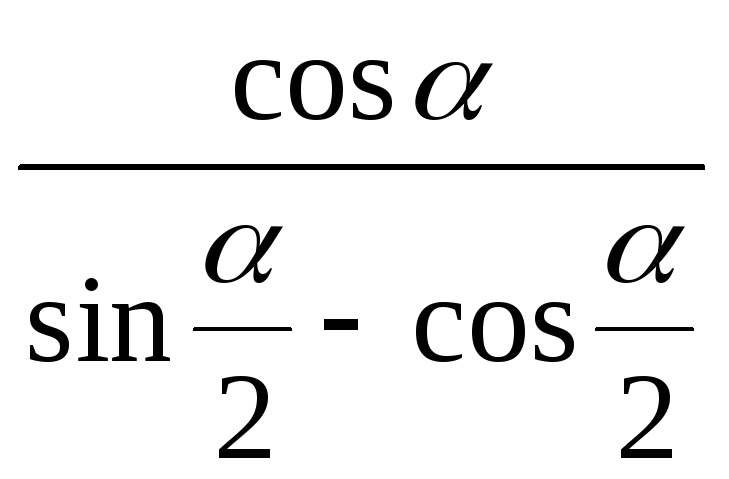
-
*
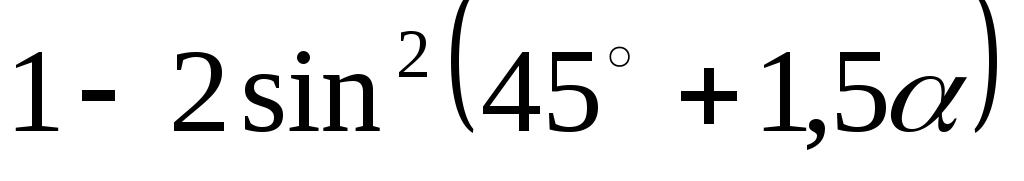
-
*
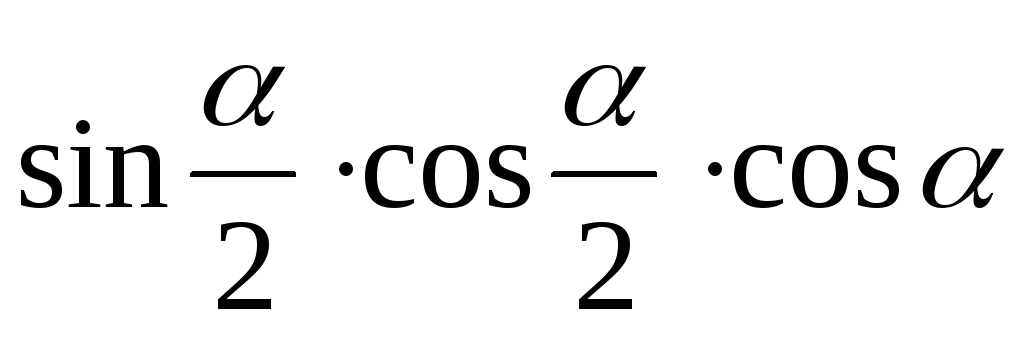
-
**
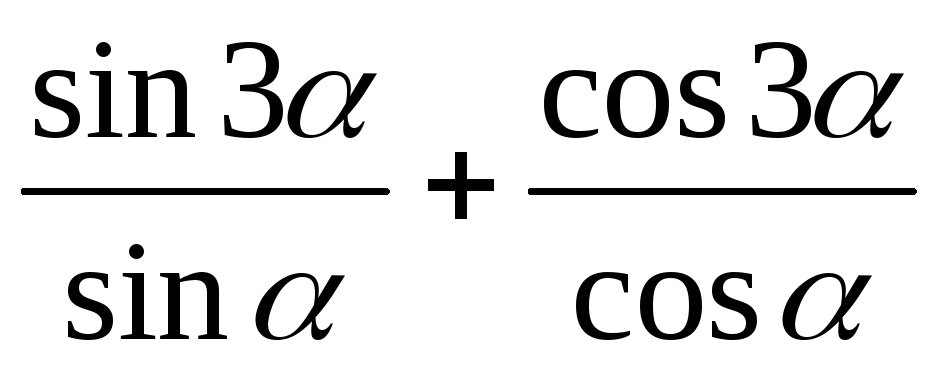
-
**
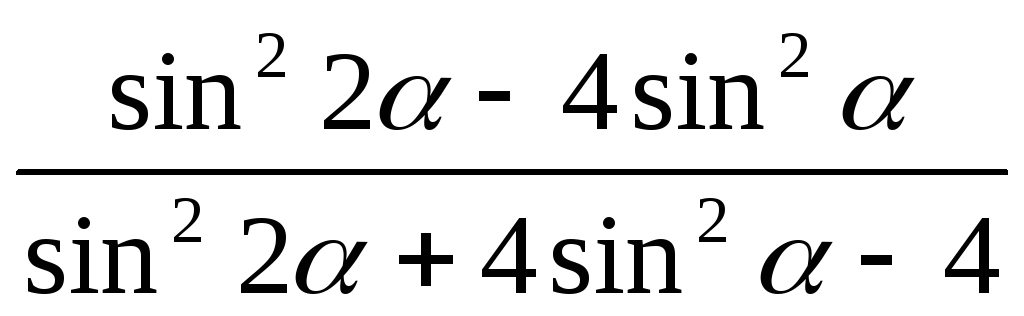
-
**
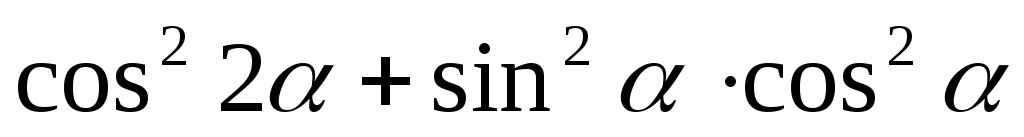
-
**
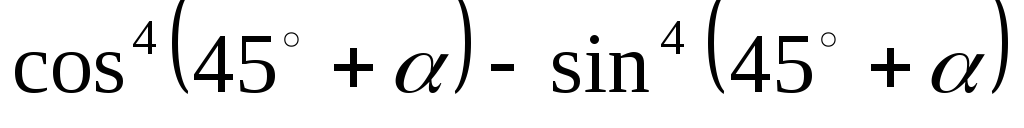
-
Довести тотожність.
-
***
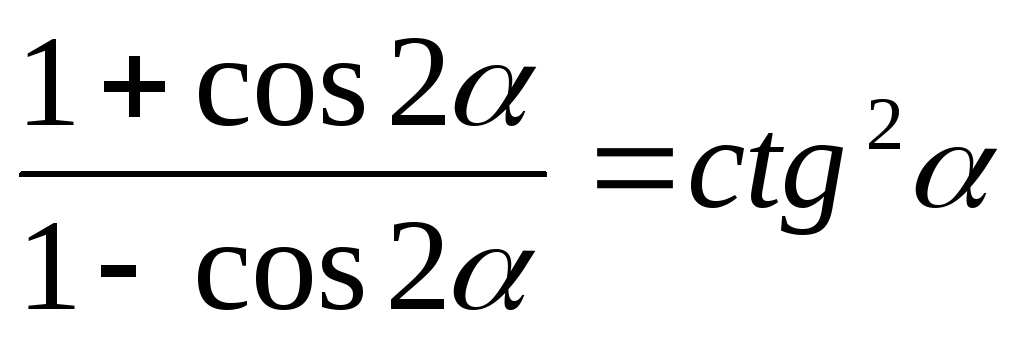
-
***
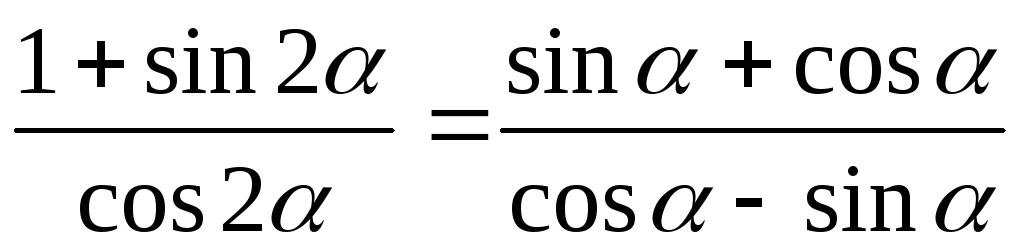
-
***
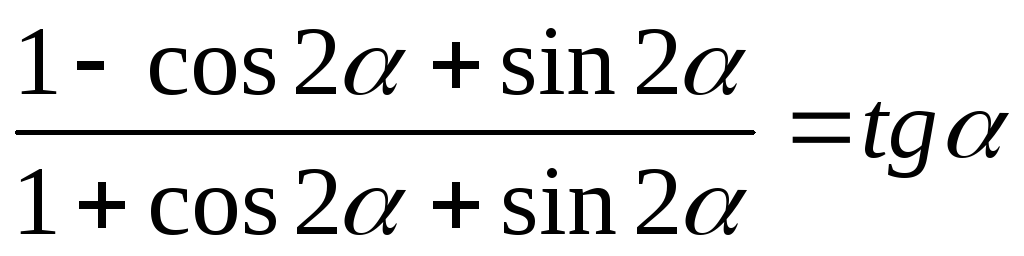
-
Знайти значення виразу.
7. Розв’яжіть найпростіші тригонометричні рівняння
1) sin x =![]() 2 cos 2x
=1 sin
2 cos 2x
=1 sin![]() = 0
= 0
2) cos x = -![]()
![]()
![]()
3) ctg 3x = 4
![]()
![]()
4)
![]()
![]()
![]()
5) sin 3x = 1 2 cos (4x)
=![]()
![]()
6)
![]() sin
2x +1 =0
sin
2x +1 =0
![]()
8. **Розв’язати рівняння, права частина яких нуль,
а ліва розкладається на множники.
9.*** Розв’язати однорідні тригонометричні рівняння.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()