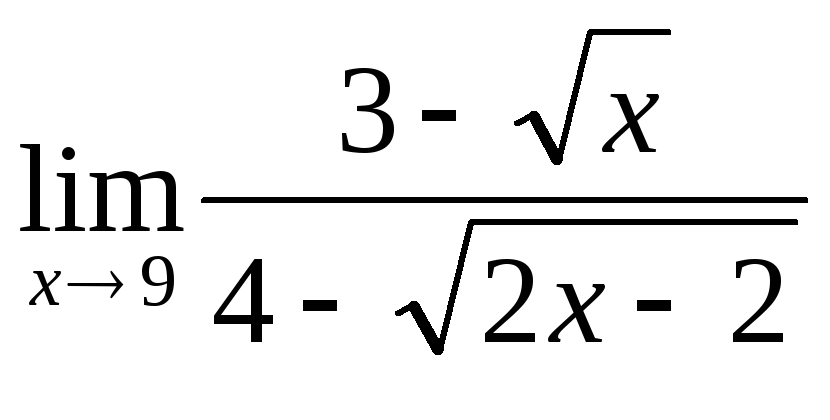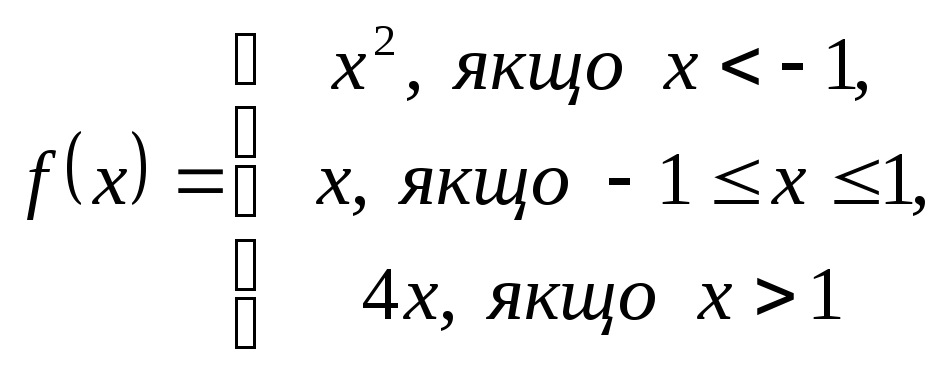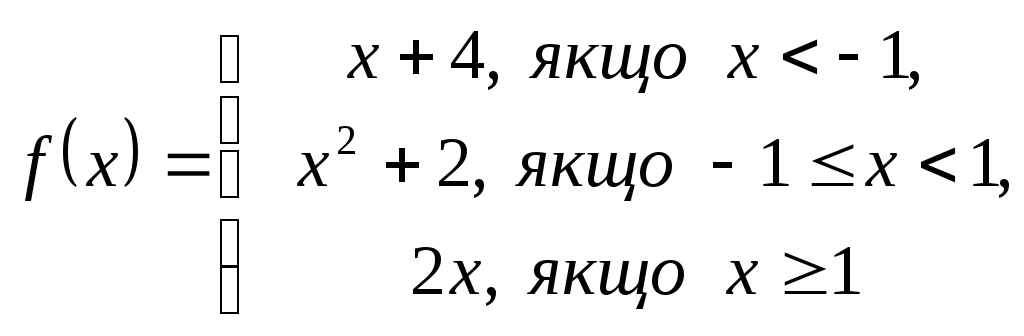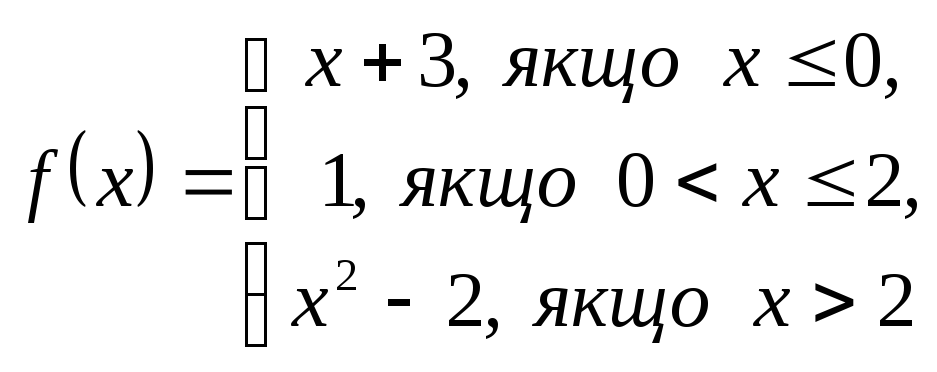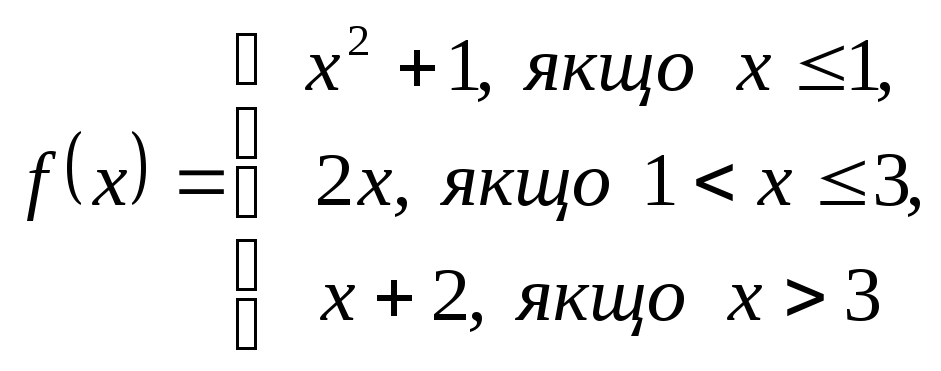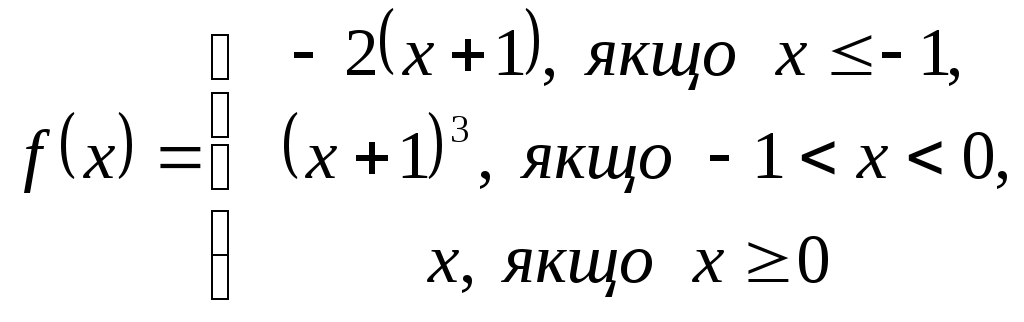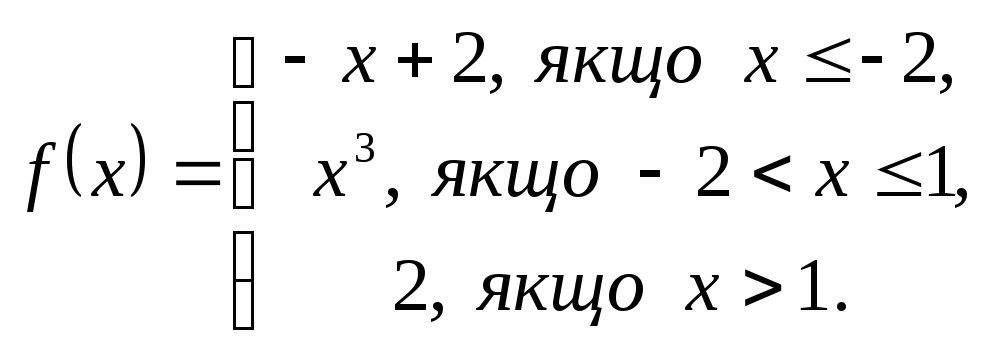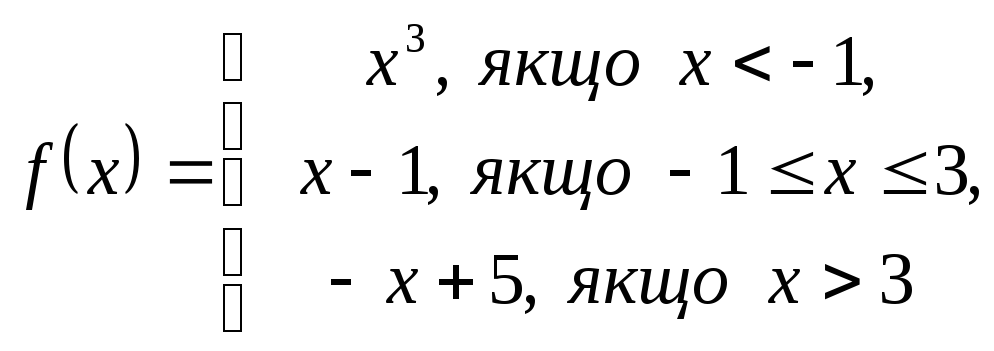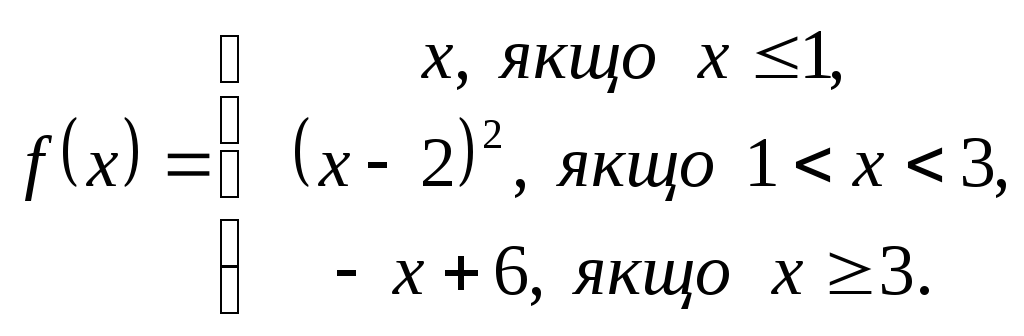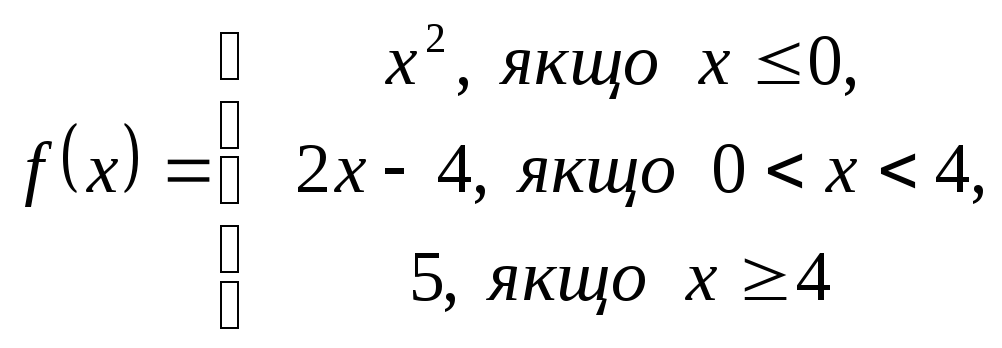- •2. Розділ 2 границі функції в точці та
- •5. Розділ 5. Похідна функції та її
- •Приклади для розв’язування.................................................44
- •6..4 Приклади для розв’язування........................................................54
- •Приклади для розв’язування.................................................64
- •Приклади для розв’язування......................................................73
- •Розділ 1. Функції, їх властивості та графіки План
- •Приклади для розв’язування.
- •Елементарні функції та їх графіки
- •4. Найпростіші перетворення графіків функцій.
- •5. Приклади для розв’язування.
- •3. Побудувати графік функції та указати область значень:
- •Розділ 2. Границі функції в точці та на нескінченності та їх використання для дослідження функцій План
- •Границя функції в точці.
- •Дослідження функції на неперервність
- •1. Границя функції в точці
- •2. Теореми про границі.
- •3. Правила обчислення границь.
- •4. Границя функції на нескінченності.
- •5.Дослідження функції на неперервність.
- •5. Приклади для розв’язування.
- •Розділ 3. Тригонометрія План
- •6. Основні формули тригонометрії.
- •7. . Найпростіші тригонометричні рівняння
- •8. Приклади для розв’язування.
- •1. Визначення тригонометричних функцій
- •Слід пам’ятати:
- •7. «Найпростіші тригонометричні рівняння»
- •8. Приклади для розв’язування.
- •Розділ 4. Степені та логарифми План
- •Приклади для розв’язування.
- •1. Степені. Корінь n-го степеня.
- •4. Поняття логарифмів .
- •6. Приклади для розв’язування
- •Розділ 5. Похідна та її використання План
- •Приклади для розв’язування
- •1. Поняття похідної функції.
- •2. Фізичний зміст похідної:
- •3. Геометричний зміст похідної.
- •4. Рівняння дотичної і нормалі до плоскої кривої.
- •Приклади для розв’язування
- •15. Знайти рівняння дотичної до графіка функції , яка паралельна прямій .
- •21. ***Задачі на знаходження найбільших та найменших значень величин.
- •Розділ 6. Інтеграл та його використання План
- •3. Таблиця невизначених інтегралів.
- •4. Визначений інтеграл.
- •1. Первісна та невизначений інтеграл.
- •2. Основні властивості невизначеного інтеграла.
- •3. Таблиця невизначених інтегралів.
- •Визначений інтеграл
- •6.Формула Ньютона – лейбніца.
- •7. Використання інтегралів для обчислення площі плоских фігур
- •Приклади для розв’язування.
- •6. Обчислити визначений інтеграл.
- •Розділ 7. Вектори та координати План
- •Вектори та дії з ними.
- •Лінійні операції над векторами.
- •Рівняння прямої на площині».
- •Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •1. Вектори та дії з ними.
- •2. Лінійні операції над векторами.
- •3. Рівняння прямої на площині».
- •4. Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •Розділ 8. . Стереометрія План
- •Приклади для розв’язування
- •Основні поняття стереометрії
- •2. Аксіоми стереометрії
- •3. Теореми стереометрії
- •4. Площі геометричних фігур.
- •5. Площі поверхонь та об’єми геометричних тіл.
- •6. Паралельні проекції деяких плоских фігур.
- •7.Приклади для розв’язування
5. Приклади для розв’язування.
1. Обчислити границі.
2. Дослідити функцію на неперервність і побудувати графік.
1.
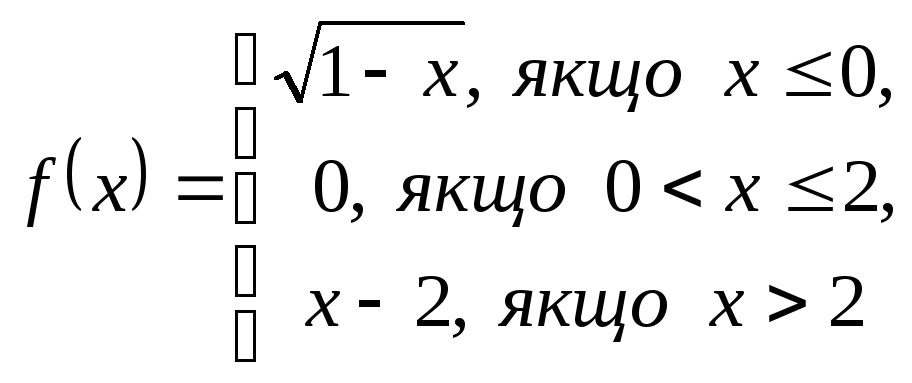
3. Обчислити границі функції в точці та на нескінченності:
1.
![]() 5.
5.
![]()
2.
![]() 6.
6.
![]()
3.
![]() 7.
7.
![]()
4.
![]() 8.
8.
![]()
Розділ 3. Тригонометрія План
1. Визначення тригонометричних функцій
2. Графіки тригонометричних функцій
3. Основні співвідношення
4. Знаки тригонометричних функцій по четвертях
5. Таблиця значень тригонометричних функцій деяких кутів
6. Основні формули тригонометрії.
7. . Найпростіші тригонометричні рівняння
8. Приклади для розв’язування.
1. Визначення тригонометричних функцій
Т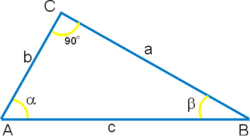 ригонометричні
функції можна визначити розглянувши
прямокутний трикутник. Косинусом кута
називається відношення довжини прилеглого
катета до довжини гіпотенузи.
ригонометричні
функції можна визначити розглянувши
прямокутний трикутник. Косинусом кута
називається відношення довжини прилеглого
катета до довжини гіпотенузи.
![]()
Тангенсом кута називається відношення довжини
протилежного катета до довжини прилеглого катета:
![]()
Котангенсом кута називається відношення
довжини прилеглого катета до довжини протилежного катета:
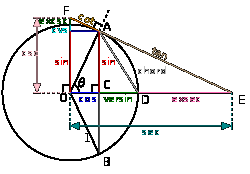
![]()
2. Графіки тригонометричних функцій
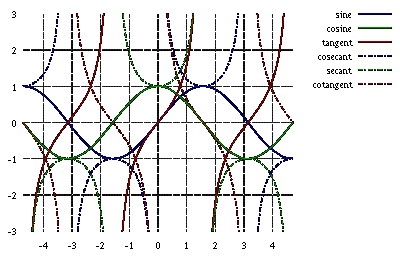
3. Основні співвідношення
Наступне співвідношення випливає із теореми Піфагора:
![]()
З урахуванням визначення , маємо як наслідок
![]()
![]()
![]()
-
Знаки тригонометричних функцій по четвертях
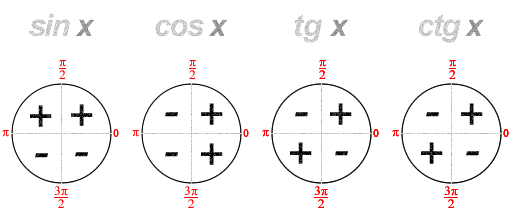
5. Таблиця значень тригонометричних функцій деяких кутів
-
α
00
300
450
600
900
1800
0 рад
π/6 рад
π/4 рад
π/3 рад
π/2 рад
π рад
Sin α
0
1/2
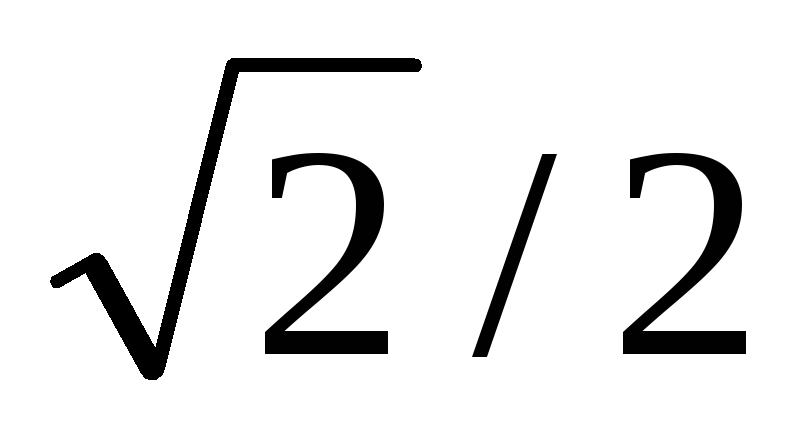
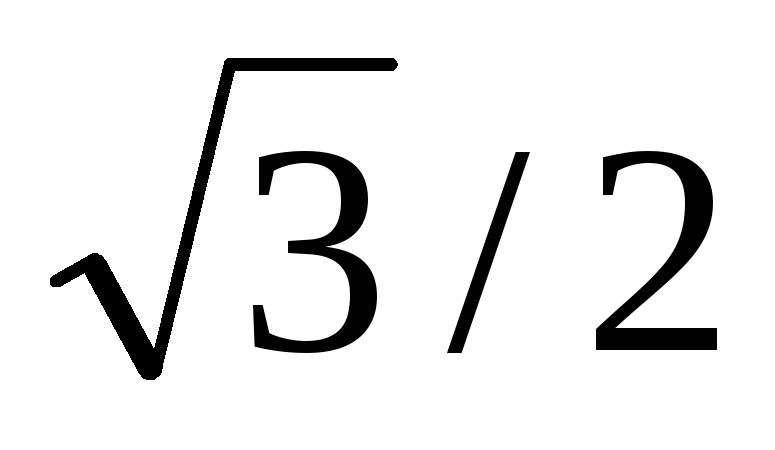
1
0
cos α
1
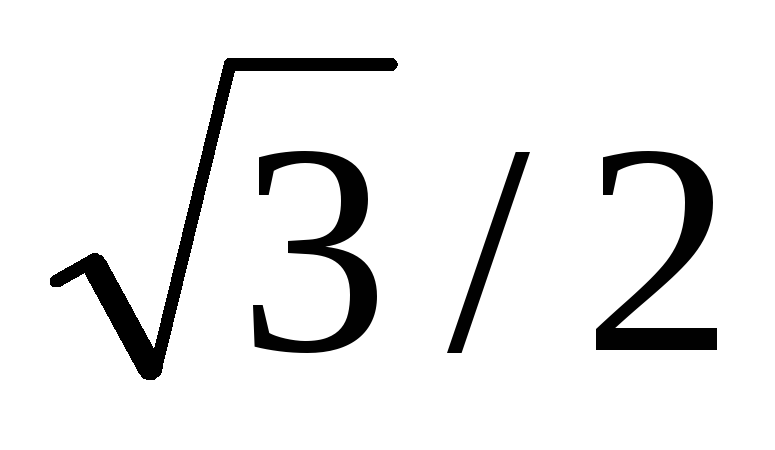
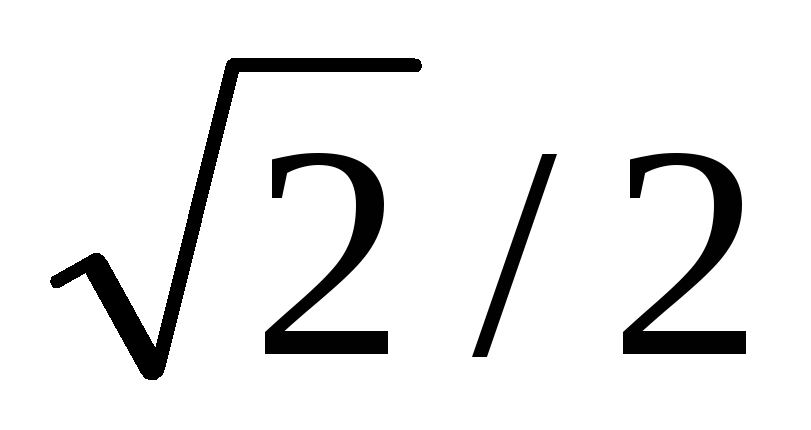
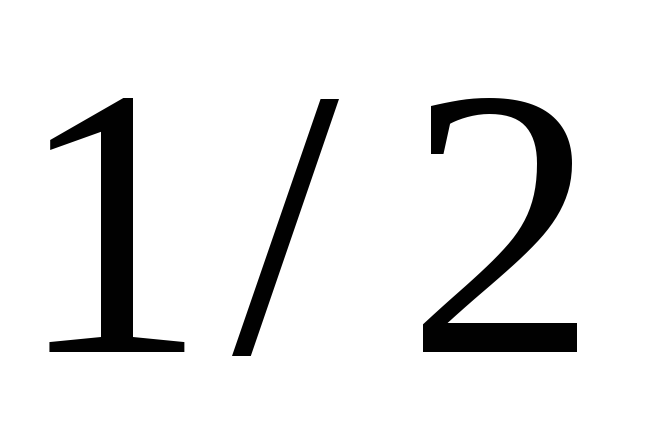
0
1
tg α
0
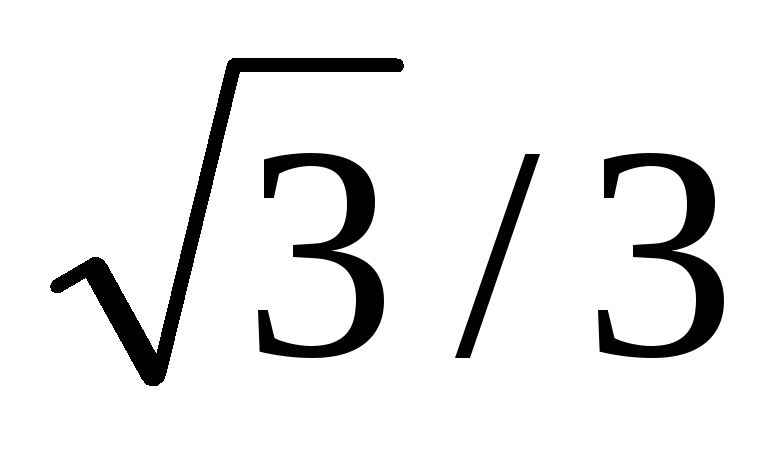
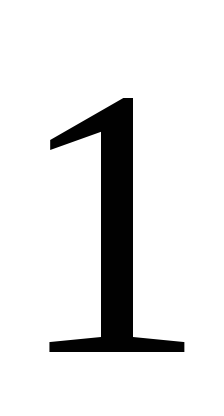
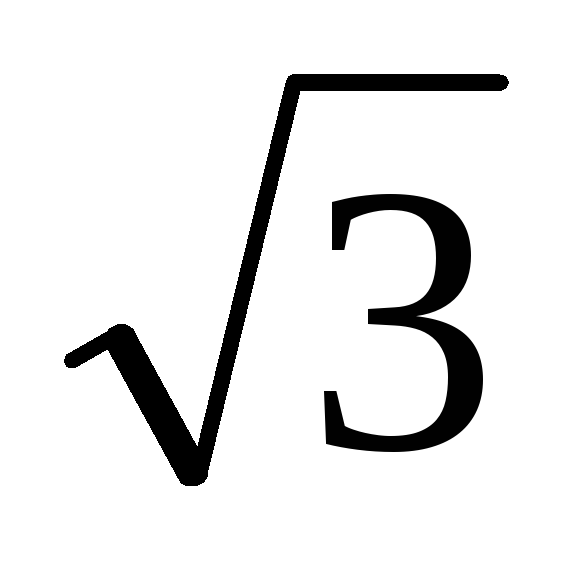
Не існ.
0
ctg α
Не існ.
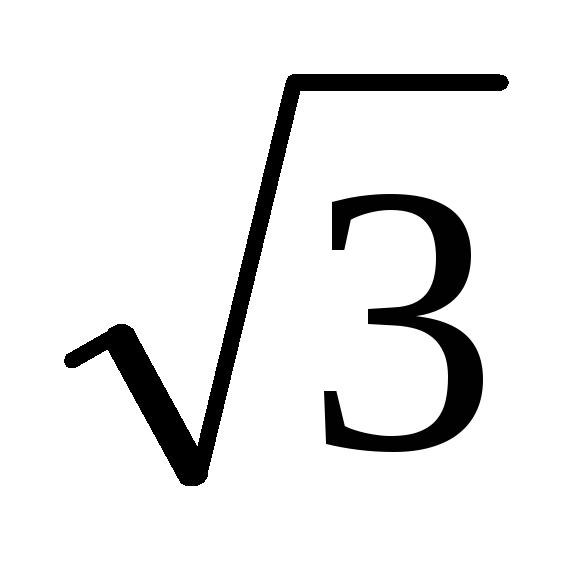
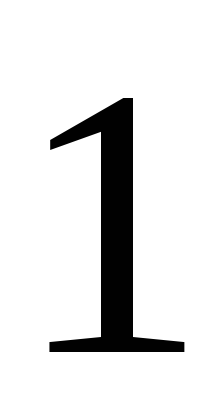
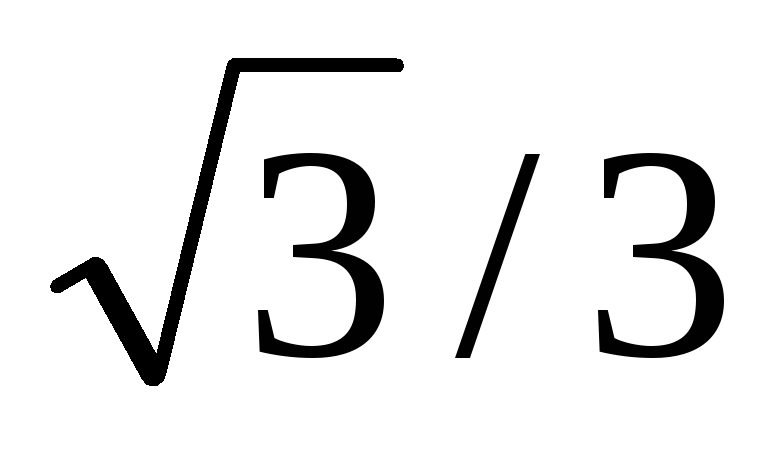
0
Не існ.