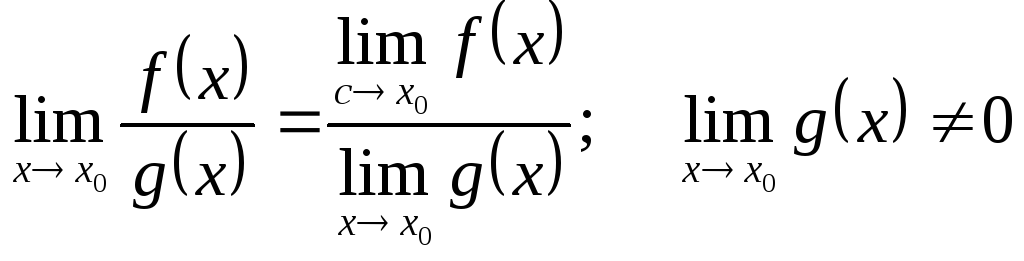- •2. Розділ 2 границі функції в точці та
- •5. Розділ 5. Похідна функції та її
- •Приклади для розв’язування.................................................44
- •6..4 Приклади для розв’язування........................................................54
- •Приклади для розв’язування.................................................64
- •Приклади для розв’язування......................................................73
- •Розділ 1. Функції, їх властивості та графіки План
- •Приклади для розв’язування.
- •Елементарні функції та їх графіки
- •4. Найпростіші перетворення графіків функцій.
- •5. Приклади для розв’язування.
- •3. Побудувати графік функції та указати область значень:
- •Розділ 2. Границі функції в точці та на нескінченності та їх використання для дослідження функцій План
- •Границя функції в точці.
- •Дослідження функції на неперервність
- •1. Границя функції в точці
- •2. Теореми про границі.
- •3. Правила обчислення границь.
- •4. Границя функції на нескінченності.
- •5.Дослідження функції на неперервність.
- •5. Приклади для розв’язування.
- •Розділ 3. Тригонометрія План
- •6. Основні формули тригонометрії.
- •7. . Найпростіші тригонометричні рівняння
- •8. Приклади для розв’язування.
- •1. Визначення тригонометричних функцій
- •Слід пам’ятати:
- •7. «Найпростіші тригонометричні рівняння»
- •8. Приклади для розв’язування.
- •Розділ 4. Степені та логарифми План
- •Приклади для розв’язування.
- •1. Степені. Корінь n-го степеня.
- •4. Поняття логарифмів .
- •6. Приклади для розв’язування
- •Розділ 5. Похідна та її використання План
- •Приклади для розв’язування
- •1. Поняття похідної функції.
- •2. Фізичний зміст похідної:
- •3. Геометричний зміст похідної.
- •4. Рівняння дотичної і нормалі до плоскої кривої.
- •Приклади для розв’язування
- •15. Знайти рівняння дотичної до графіка функції , яка паралельна прямій .
- •21. ***Задачі на знаходження найбільших та найменших значень величин.
- •Розділ 6. Інтеграл та його використання План
- •3. Таблиця невизначених інтегралів.
- •4. Визначений інтеграл.
- •1. Первісна та невизначений інтеграл.
- •2. Основні властивості невизначеного інтеграла.
- •3. Таблиця невизначених інтегралів.
- •Визначений інтеграл
- •6.Формула Ньютона – лейбніца.
- •7. Використання інтегралів для обчислення площі плоских фігур
- •Приклади для розв’язування.
- •6. Обчислити визначений інтеграл.
- •Розділ 7. Вектори та координати План
- •Вектори та дії з ними.
- •Лінійні операції над векторами.
- •Рівняння прямої на площині».
- •Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •1. Вектори та дії з ними.
- •2. Лінійні операції над векторами.
- •3. Рівняння прямої на площині».
- •4. Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •Розділ 8. . Стереометрія План
- •Приклади для розв’язування
- •Основні поняття стереометрії
- •2. Аксіоми стереометрії
- •3. Теореми стереометрії
- •4. Площі геометричних фігур.
- •5. Площі поверхонь та об’єми геометричних тіл.
- •6. Паралельні проекції деяких плоских фігур.
- •7.Приклади для розв’язування
2. Теореми про границі.
Якщо кожна з
функцій
![]() і
і
![]() має скінченну границю при
має скінченну границю при
![]()
![]() ,
то справедливі формули:
,
то справедливі формули:
3. Правила обчислення границь.
-
Якщо функція дробово – раціональна, то для знаходження границі чисельник і знаменник розкладають на множники, які потім скорочують, причому скоротитись повинен той множник, який обертається в нуль.
![]()
-
Якщо чисельник функції – стала величина, а границя знаменника дорівнює нулю, то границя такої функції є нескінченність.
![]()
-
Якщо функція містить знаки радикалів, то чисельник і знаменник помножають на вираз, спряжений до чисельника (знаменника), а потім застосовують формулу різниці квадратів. Вирази
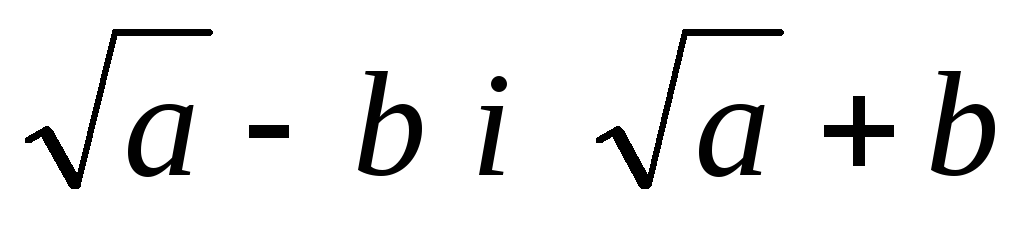 та
та
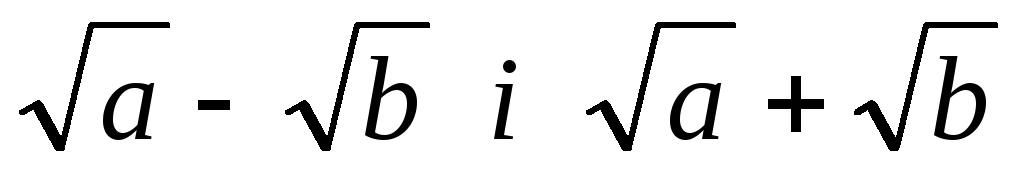 називаються спряженими.
називаються спряженими.
![]()
![]()
-
Якщо функція містить корінь третього степеня, то чисельник і знаменник помножають на неповний квадрат суми або різниці, а потім застосовують формулу суми або різниці кубів.
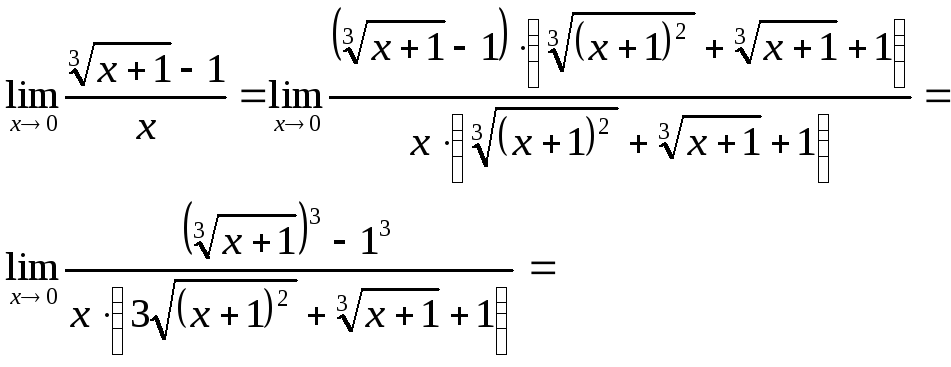
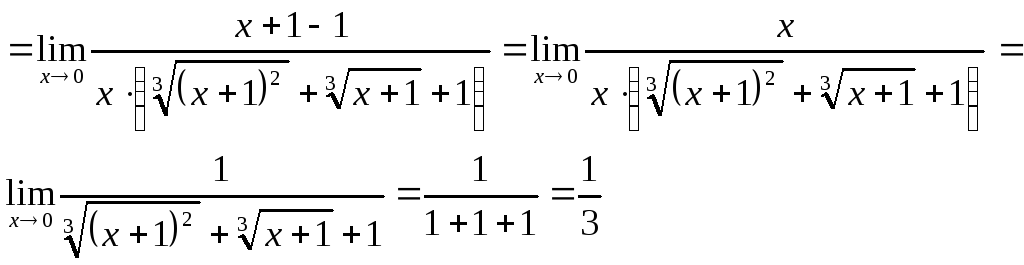
4. Границя функції на нескінченності.
Границею на нескінченності називається число, до якого прямує значення функції, якщо аргумент нескінченно зростає.
-
Границя функції, яка представляє собою многочлен, при
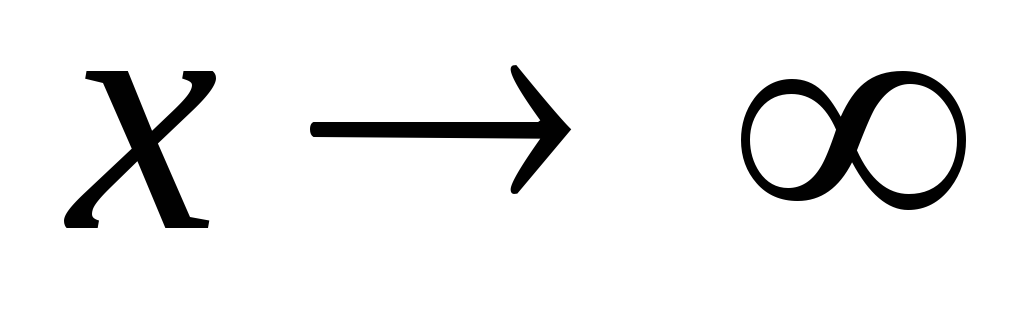 є нескінченність.
є нескінченність.
![]()
-
Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника і знаменника однакові дорівнює відношенню коефіцієнтів при старших членах.
![]()
-
Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника менша за степінь знаменника, дорівнює нулю.
![]()
-
Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника більша за степінь знаменника, дорівнює нескінченності.
![]()
5.Дослідження функції на неперервність.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,
якщо вона в цій точці визначена і
нескінченно малому приросту аргументу
відповідає нескінченно малий приріст
функції:
,
якщо вона в цій точці визначена і
нескінченно малому приросту аргументу
відповідає нескінченно малий приріст
функції:
![]() .
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,якщо
виконуються слідуючи умови:
,якщо
виконуються слідуючи умови:
-
функція визначена в точці
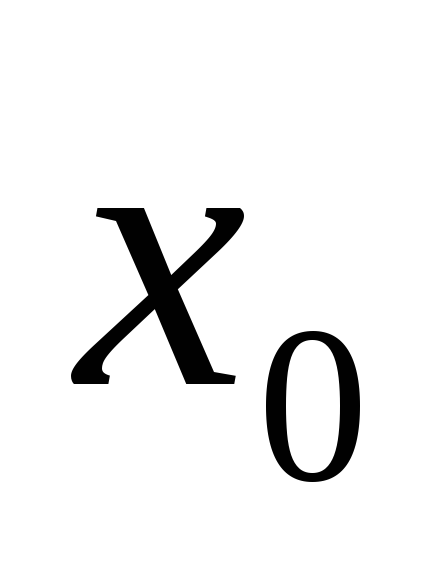 ;
; -
існує границя функції в точці
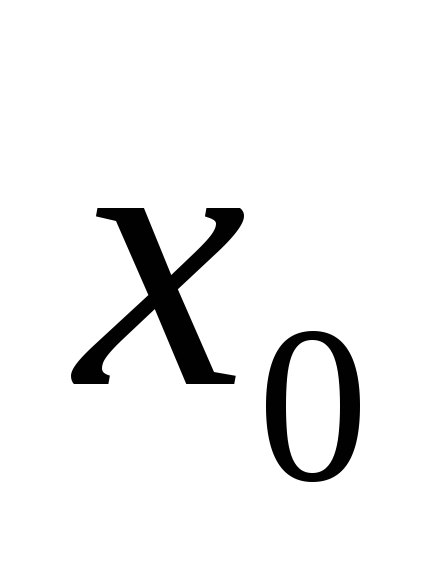 ;
; -
значення функції в точці
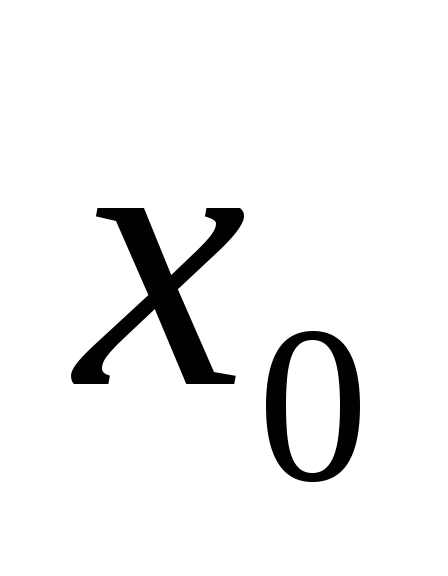 співпадає із значенням границі в точці
співпадає із значенням границі в точці
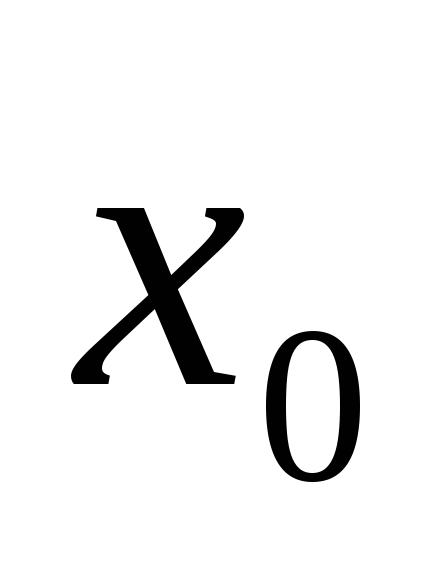 .
.
Число А
називається
границею
функції
![]() справа при
справа при
![]() ,
,
![]()
![]() ,
якщо функція визначена у правому
,
якщо функція визначена у правому
![]() -
околі точки
-
околі точки
![]() ,
і для будь – якого
,
і для будь – якого
![]() знайдеться таке
знайдеться таке
![]() ,
що для всіх
,
що для всіх
![]() ,
взятих з інтервалу
,
взятих з інтервалу
![]() виконується нерівність
виконується нерівність
![]() .
.
Позначають
![]()
Число А
називається
границею
функції
![]() зліва при
зліва при
![]() ,
,
![]()
![]() ,
якщо функція визначена у лівому
,
якщо функція визначена у лівому
![]() -
околі точки
-
околі точки
![]() ,
і для будь – якого
,
і для будь – якого
![]() знайдеться таке
знайдеться таке
![]() ,
що для всіх
,
що для всіх
![]() ,
взятих з інтервалу
,
взятих з інтервалу
![]() виконується нерівність
виконується нерівність
![]() .
.
Позначають
![]()
Функція
![]() називається неперервною
в точці
називається неперервною
в точці
![]() ,якщо
виконуються слідуючи умови:
,якщо
виконуються слідуючи умови:
-
функція визначена в точці
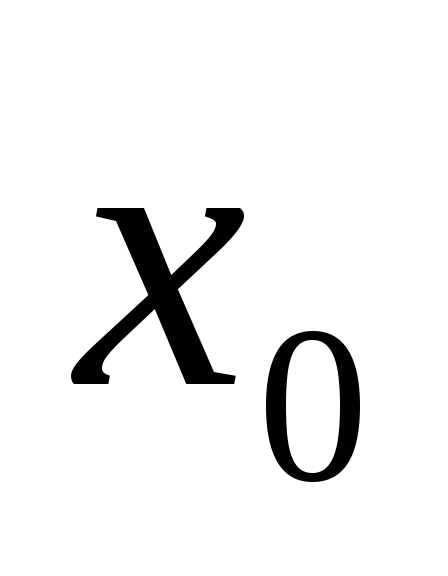 і
в деякому околі цієї точки;
і
в деякому околі цієї точки; -
існують односторонні границі
 і
і
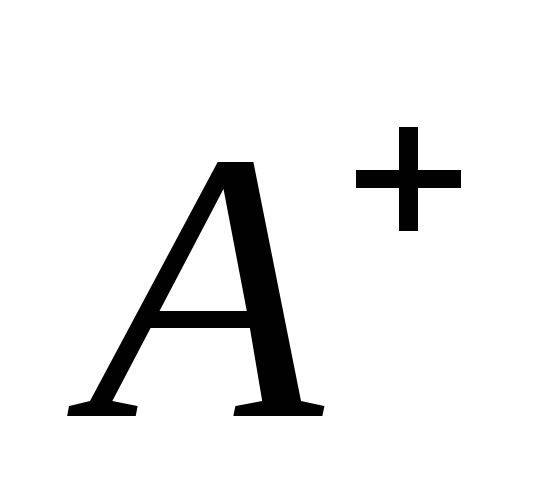 ;
; -
односторонні границі рівні між собою і дорівнюють значенню функції в точці
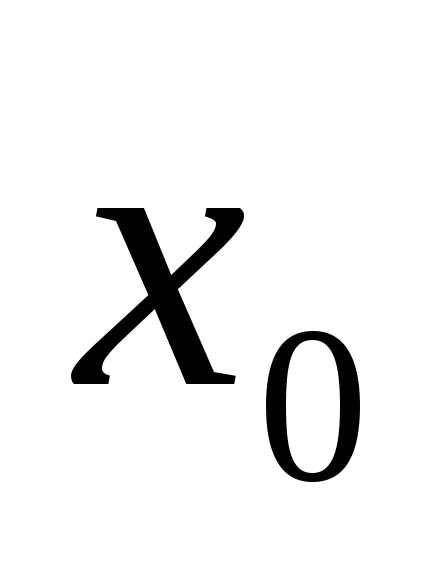 .
.