5. Приклади для розв’язування......................................................73

Рівні засвоєння навчального матеріалу:

• перший рівень – початковий – відповідь студента при відтворенні навчального матеріалу – елементарна, фрагментарна, зумовлюється початковими уявленнями про предмет вивчення;

• другий рівень – середній – студент відтворює основний навчальний матеріал, здатний розв’язувати завдання за зразком, володіє елементарними вміннями навчальної діяльності (*);

• третій рівень – достатній – студент знає істотні ознаки понять, явищ, закономірностей зв’язків між ними, а також самостійно застосовує знання в стандартних ситуаціях, володіє розумовими операціями (аналізом, абстрагуванням, узагальненням тощо), уміє робити висновки, виправляти допущені помилки; відповідь повна, правильна, логічна, обгрунтована, хоча їй бракує власних суджень (**);

• четвертий рівень – високий – знання студента є глибокими, міцними, узагальненими, системними; студент уміє застосовувати знання творчо, його навчальна діяльність має дослідницький характер, позначена вмінням самостійно оцінювати різноманітні життєві ситуації, явища, факти, виявляє і відстоює особисту позицію (***).

Розділ 1. Функції, їх властивості та графіки План

1. Визначення функції та способи задання.

2. Властивості функції.

3. Графіки елементарних функцій та їх властивості.

4. Перетворення графіків елементарних функцій

5. Приклади для розв’язування.

1. Функцією називається відповідність між двома множинами, при якій кожному елементу однієї множини ( області визначення ) відповідає єдиний елемент іншої множини ( області значень ).

Область визначення функції має обмеження у таких випадках:

• 

• 

• 

2. Функція зростає, якщо більшому значенню аргумента відповідає більше значення функції і спадає в іншому випадку:

f(x) ↑↔ x₂>x₁→ f(x₂)>f(x₁);

f(x) ↓↔ x₂>x₁→ f(x₂)<f(x₁);

Функція парна, якщо при зміні значення аргументу на протилежне значення функції не змінюється: f (-x) =f(x).

Функція непарна, якщо при зміні значення аргументу на протилежне значення функції змінюється на протилежне: f (-x) = - f(x).

Функція, що не являється непарною та парною називається функцією загального вигляду.

3. Елементарні функції та їх графіки

№ п/п	Назва функції.	Формула.	Графік.
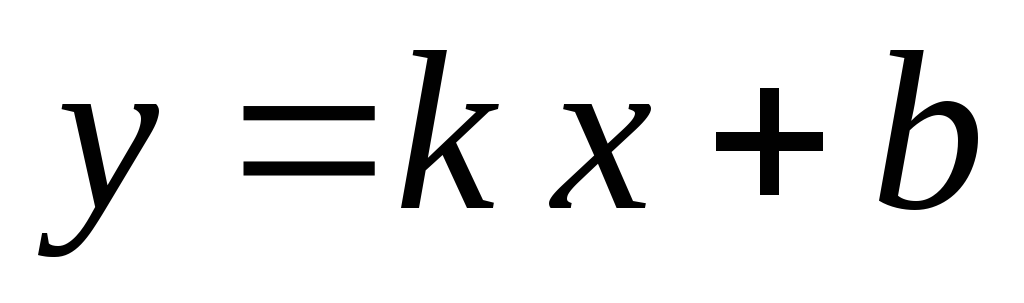
1.	Лінійна функція		Пряма лінія.
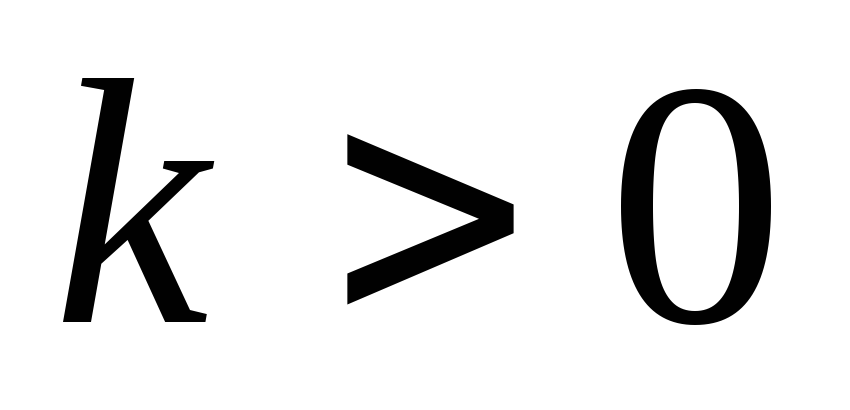
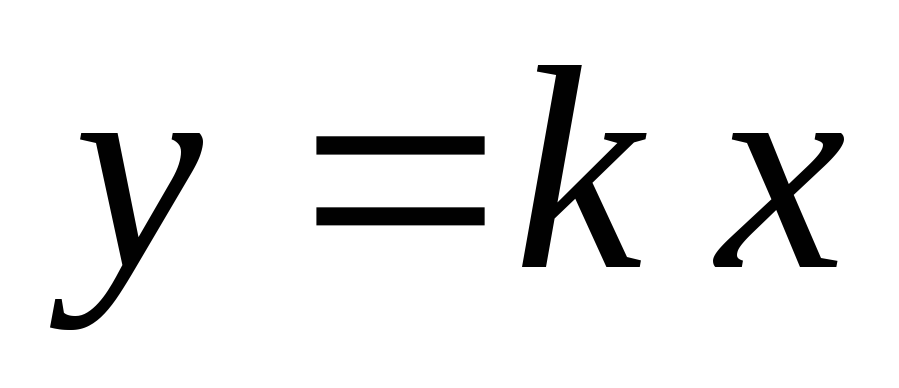
2.	Пряма пропорційність.		Пряма лінія, що проходить через початок координат.
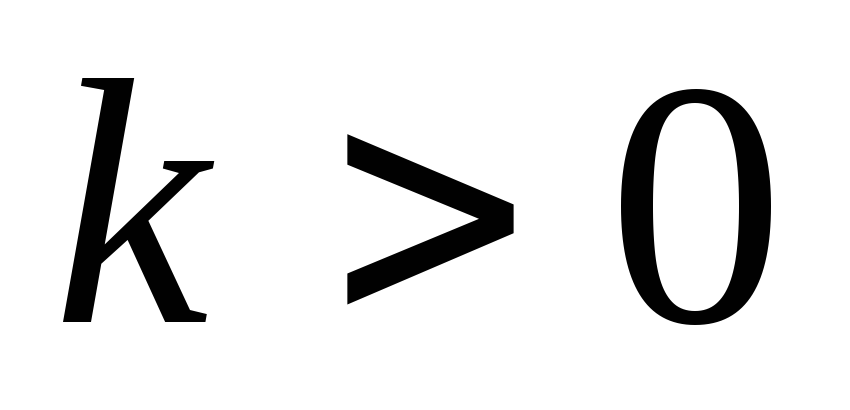
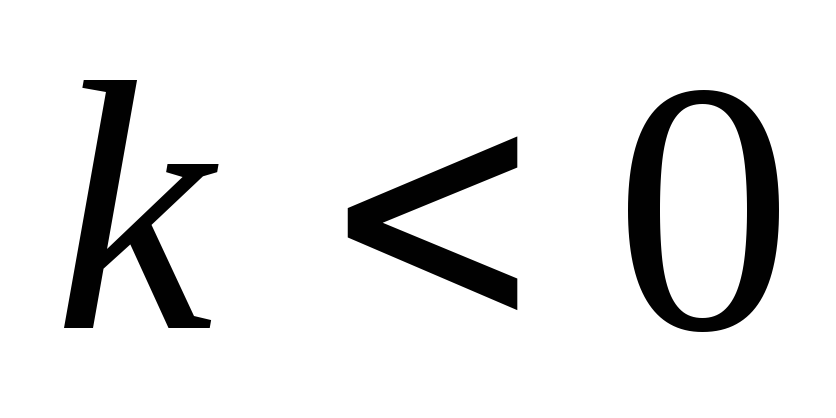
3.	Обернена пропорційність.		Гіпербола.
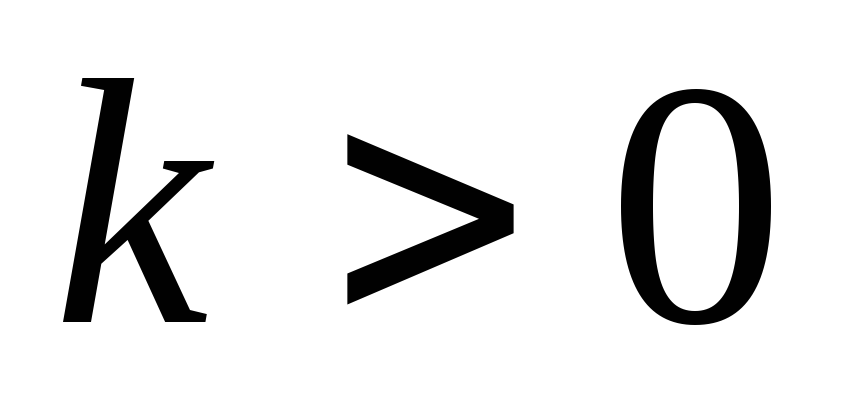
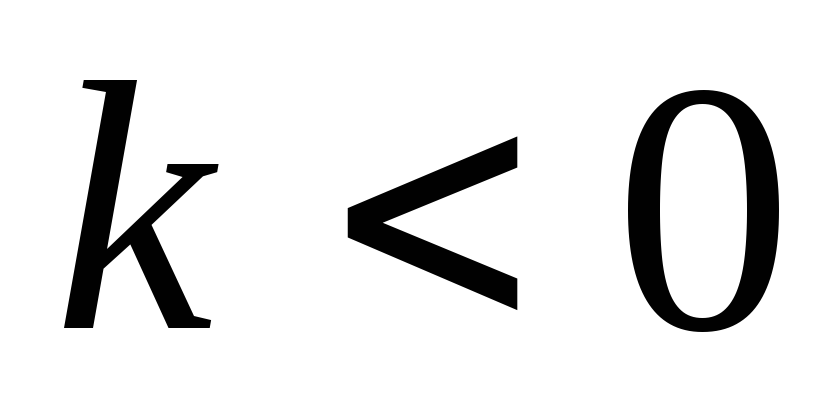
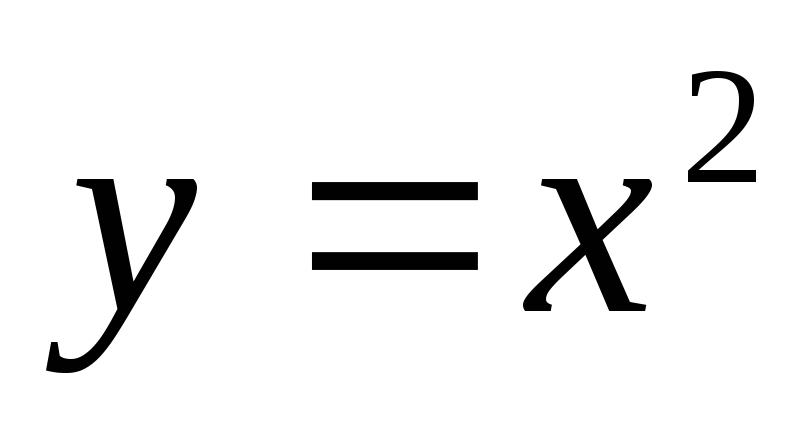
4.			Парабола.
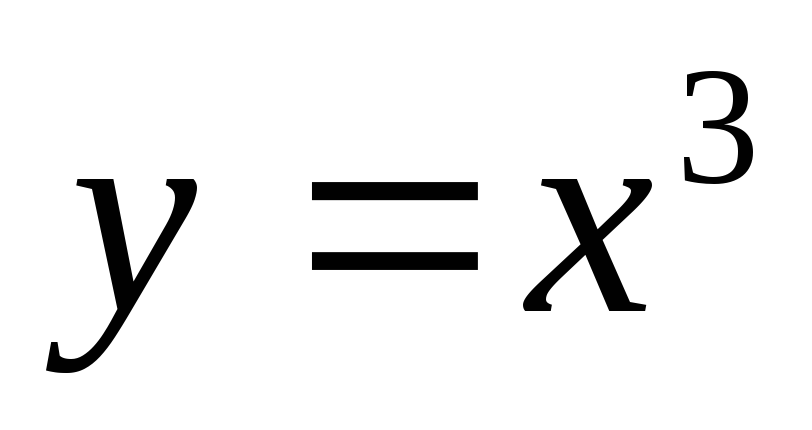
5.			Кубічна парабола.
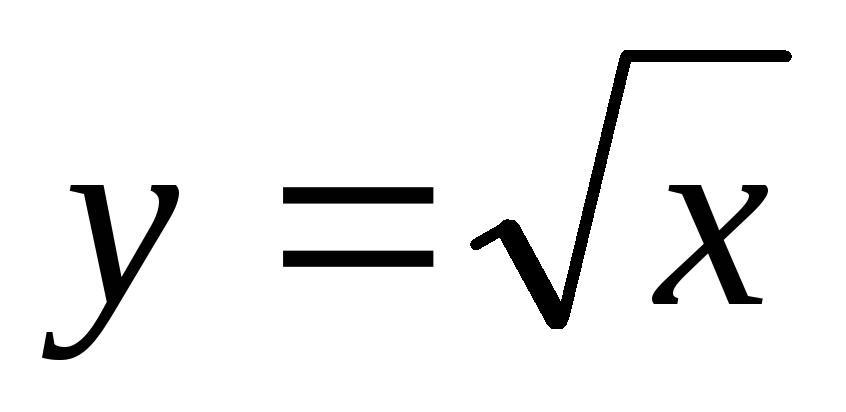
6.			«Лежача» вітка параболи
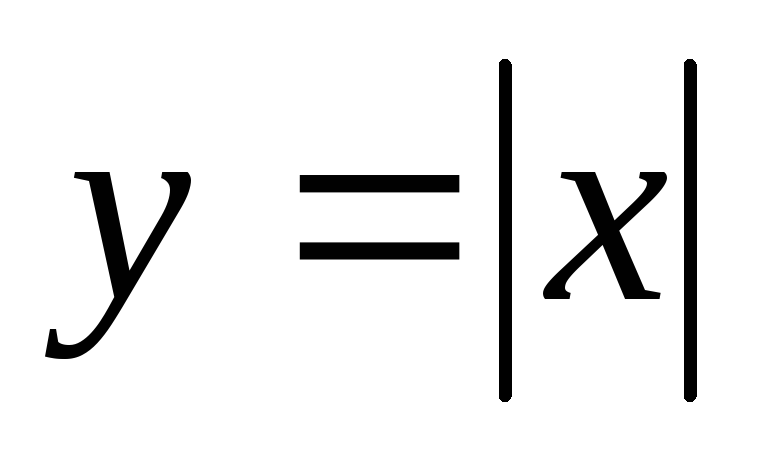
7.			Кут, утворений бісектрисами 1 та 2 чверті.