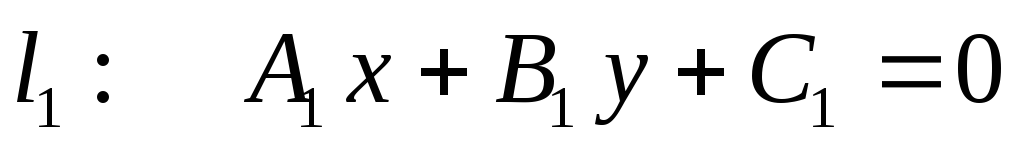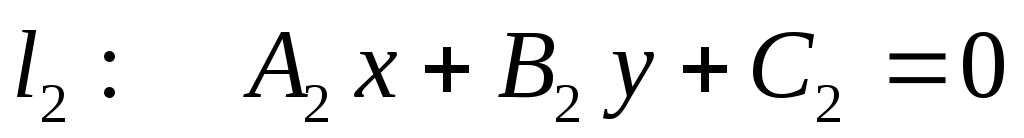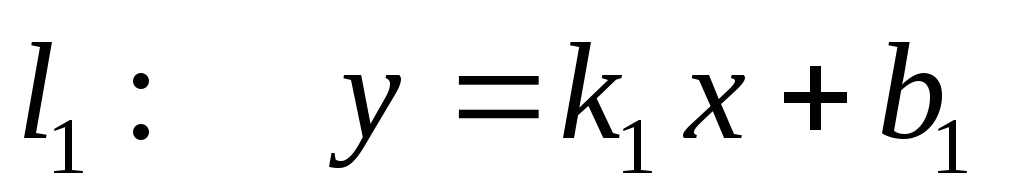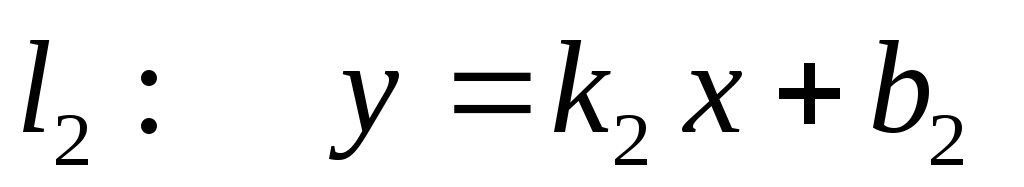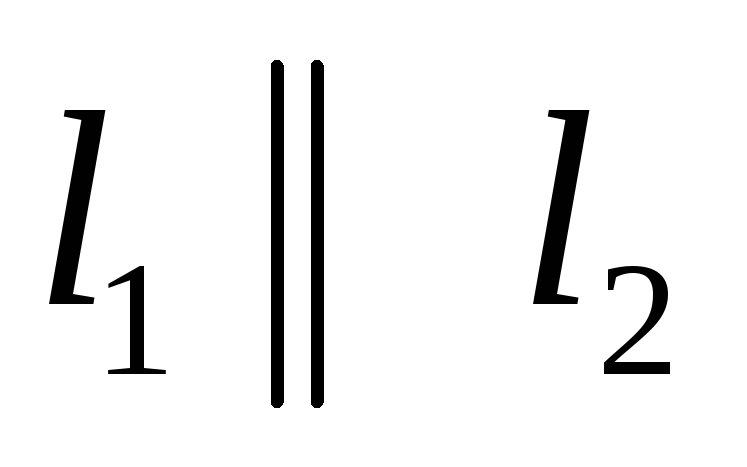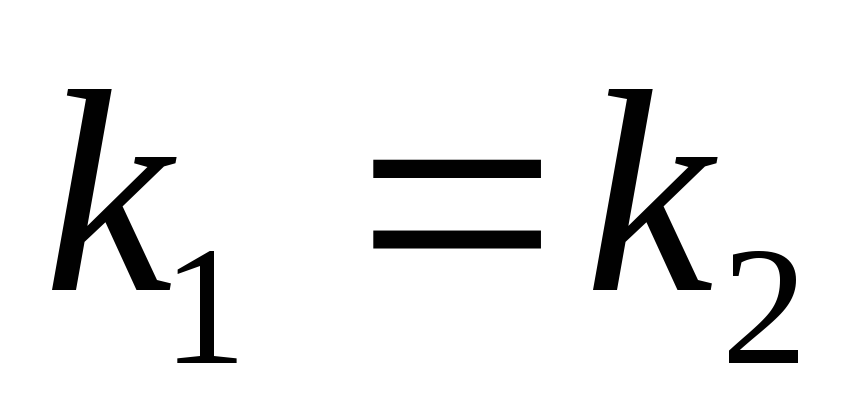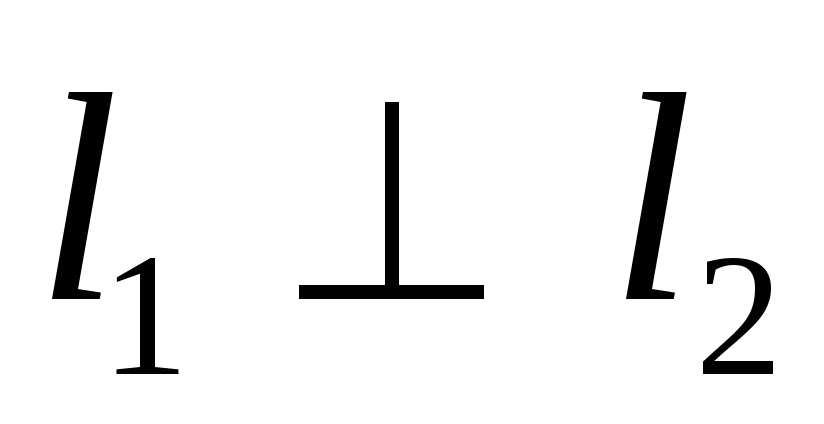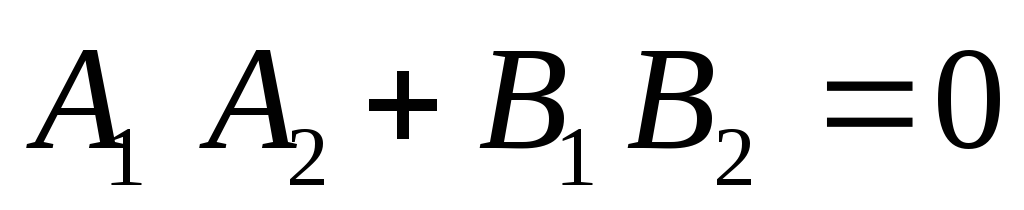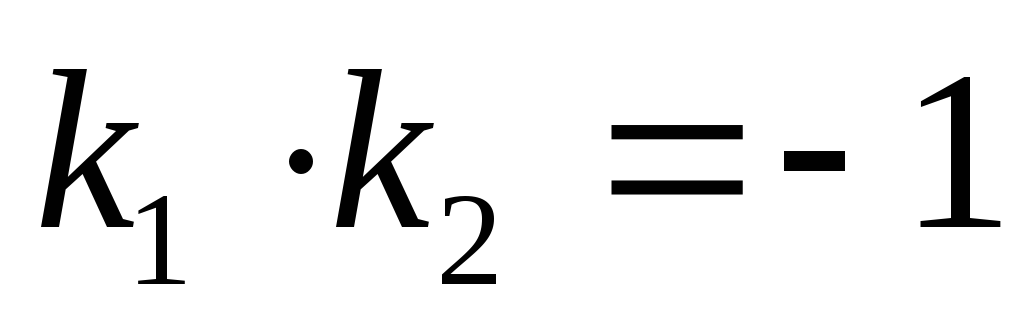- •2. Розділ 2 границі функції в точці та
- •5. Розділ 5. Похідна функції та її
- •Приклади для розв’язування.................................................44
- •6..4 Приклади для розв’язування........................................................54
- •Приклади для розв’язування.................................................64
- •Приклади для розв’язування......................................................73
- •Розділ 1. Функції, їх властивості та графіки План
- •Приклади для розв’язування.
- •Елементарні функції та їх графіки
- •4. Найпростіші перетворення графіків функцій.
- •5. Приклади для розв’язування.
- •3. Побудувати графік функції та указати область значень:
- •Розділ 2. Границі функції в точці та на нескінченності та їх використання для дослідження функцій План
- •Границя функції в точці.
- •Дослідження функції на неперервність
- •1. Границя функції в точці
- •2. Теореми про границі.
- •3. Правила обчислення границь.
- •4. Границя функції на нескінченності.
- •5.Дослідження функції на неперервність.
- •5. Приклади для розв’язування.
- •Розділ 3. Тригонометрія План
- •6. Основні формули тригонометрії.
- •7. . Найпростіші тригонометричні рівняння
- •8. Приклади для розв’язування.
- •1. Визначення тригонометричних функцій
- •Слід пам’ятати:
- •7. «Найпростіші тригонометричні рівняння»
- •8. Приклади для розв’язування.
- •Розділ 4. Степені та логарифми План
- •Приклади для розв’язування.
- •1. Степені. Корінь n-го степеня.
- •4. Поняття логарифмів .
- •6. Приклади для розв’язування
- •Розділ 5. Похідна та її використання План
- •Приклади для розв’язування
- •1. Поняття похідної функції.
- •2. Фізичний зміст похідної:
- •3. Геометричний зміст похідної.
- •4. Рівняння дотичної і нормалі до плоскої кривої.
- •Приклади для розв’язування
- •15. Знайти рівняння дотичної до графіка функції , яка паралельна прямій .
- •21. ***Задачі на знаходження найбільших та найменших значень величин.
- •Розділ 6. Інтеграл та його використання План
- •3. Таблиця невизначених інтегралів.
- •4. Визначений інтеграл.
- •1. Первісна та невизначений інтеграл.
- •2. Основні властивості невизначеного інтеграла.
- •3. Таблиця невизначених інтегралів.
- •Визначений інтеграл
- •6.Формула Ньютона – лейбніца.
- •7. Використання інтегралів для обчислення площі плоских фігур
- •Приклади для розв’язування.
- •6. Обчислити визначений інтеграл.
- •Розділ 7. Вектори та координати План
- •Вектори та дії з ними.
- •Лінійні операції над векторами.
- •Рівняння прямої на площині».
- •Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •1. Вектори та дії з ними.
- •2. Лінійні операції над векторами.
- •3. Рівняння прямої на площині».
- •4. Розв’язання систем лінійних рівнянь за формулами Крамера
- •5. Приклади для розв’язування.
- •Розділ 8. . Стереометрія План
- •Приклади для розв’язування
- •Основні поняття стереометрії
- •2. Аксіоми стереометрії
- •3. Теореми стереометрії
- •4. Площі геометричних фігур.
- •5. Площі поверхонь та об’єми геометричних тіл.
- •6. Паралельні проекції деяких плоских фігур.
- •7.Приклади для розв’язування
Розділ 7. Вектори та координати План
-
Вектори та дії з ними.
-
Лінійні операції над векторами.
-
Рівняння прямої на площині».
-
Розв’язання систем лінійних рівнянь за формулами Крамера
5. Приклади для розв’язування.
1. Вектори та дії з ними.
В
В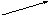
![]() ,
точка А – початок вектора, точка В –
кінець вектора.
,
точка А – початок вектора, точка В –
кінець вектора.
А
Нульовий вектор
– це вектор, у якого початок і кінець
співпадають:
![]() .
.
Довжина вектора
(модуль, абсолютна величина) - це довжина
відрізка, який зображає даний вектор:
![]() .
.
Координатами вектора називаються його проекції на осі координат.
![]() ,
де
,
де
![]() -
одиничні вектори, орти.
-
одиничні вектори, орти.
Якщо
![]() і
і
![]() ,
то координати вектора
,
то координати вектора
![]() знаходяться за формулою:
знаходяться за формулою:
![]()
Два вектори називаються рівними, якщо вони колінеарні, однаково напрямлені та рівні по довжині
Рівні вектори мають рівні координати.
Довжина вектора:
![]() ,
(якщо
,
(якщо
![]() ,
то
,
то
![]() ).
).
Вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Якщо вектори
![]() і
і
![]() колінеарні, то їх координати пропорційні
колінеарні, то їх координати пропорційні
![]() .
.
2. Лінійні операції над векторами.
-
Вектор.
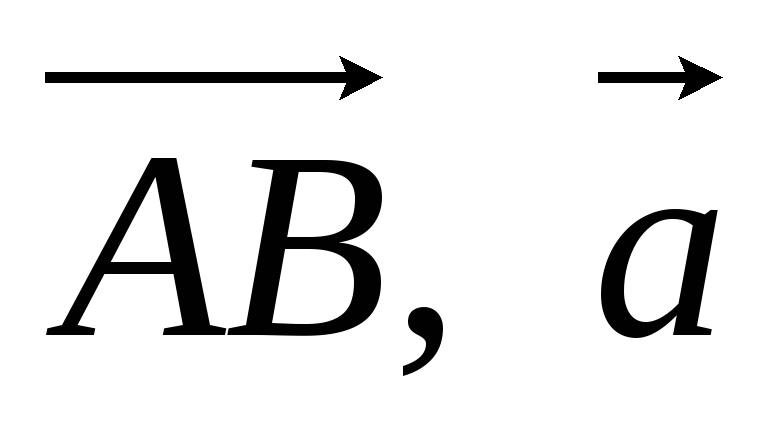
Координати вектора.
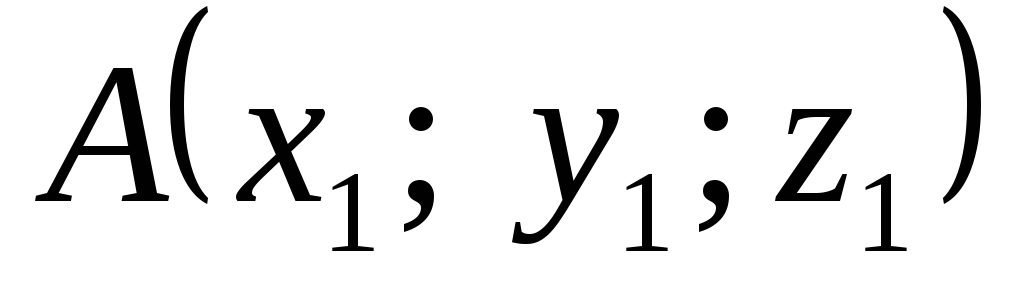 і
і
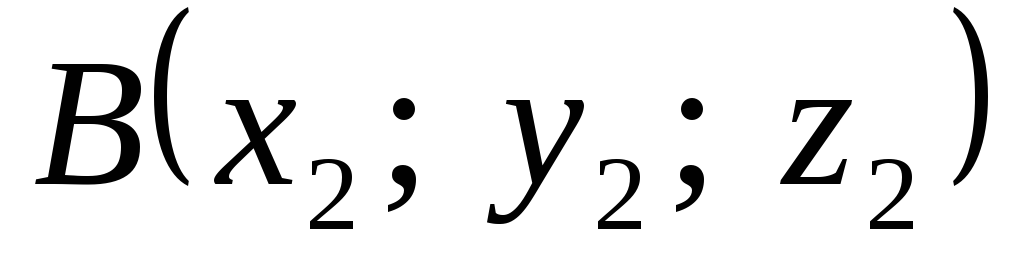 ,
,
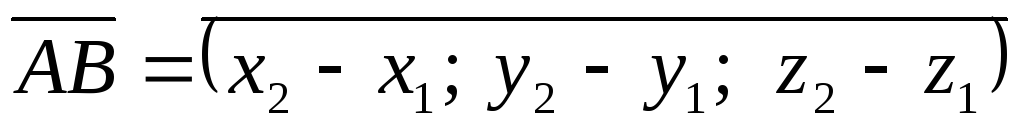
Довжина вектора.
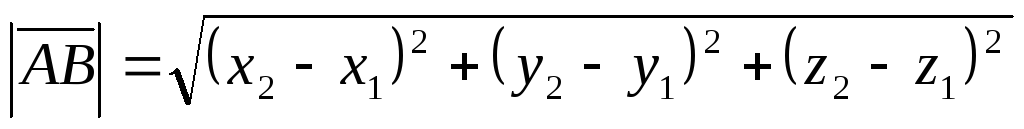
якщо
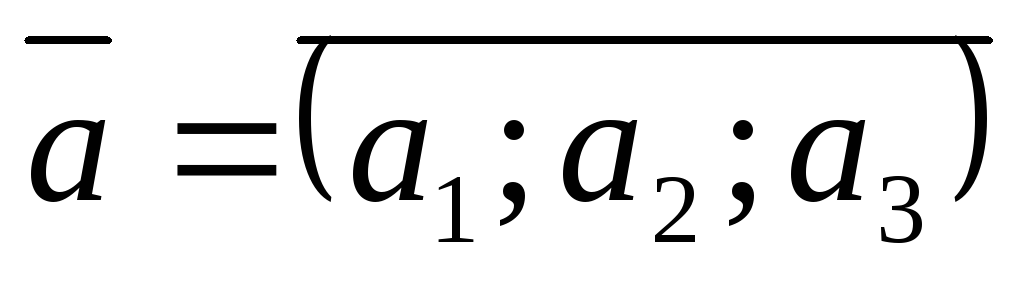 ,
то
,
то
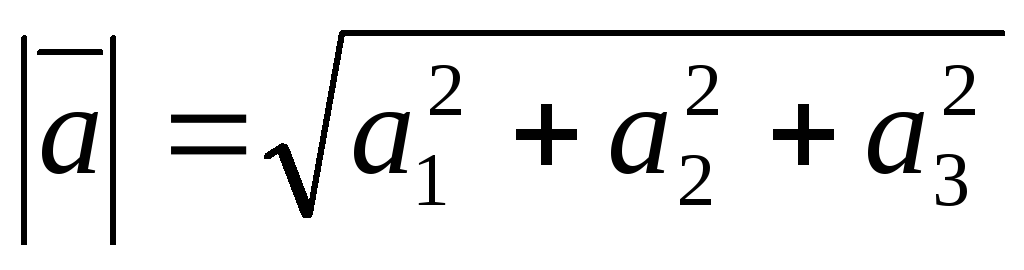 .
.Додавання векторів.
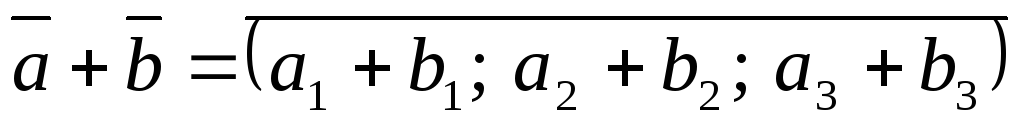
Віднімання векторів.
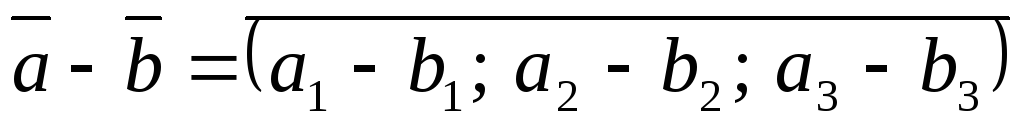
Множення вектора на число.
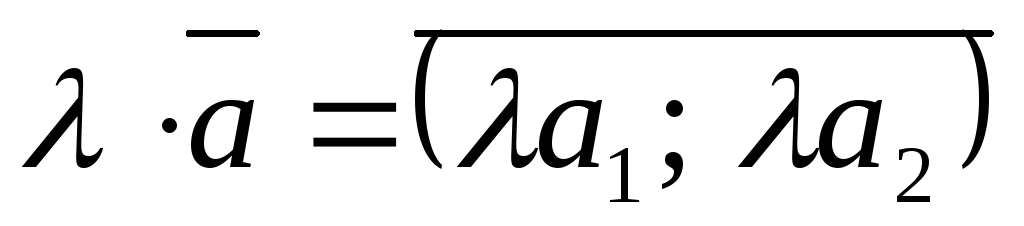
Скалярний добуток векторів (означення)
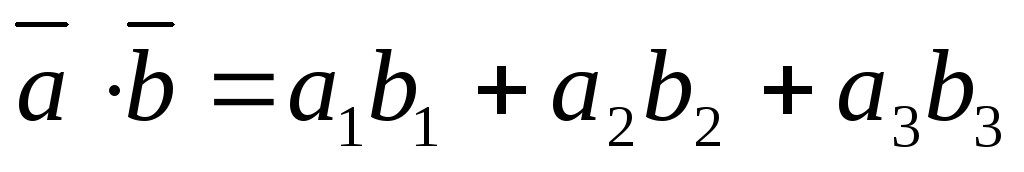
Теорема про скалярний добуток векторів
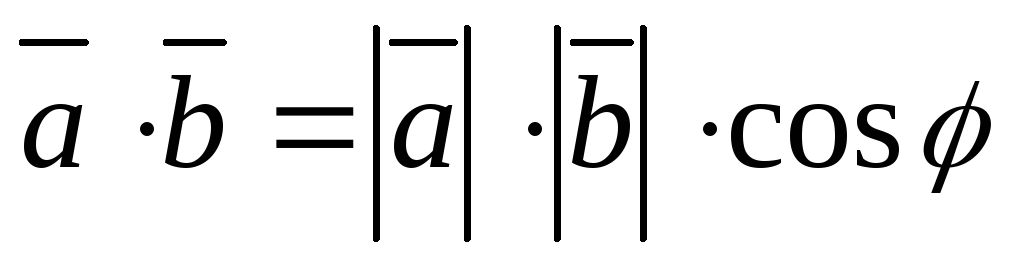
Кут між векторами.
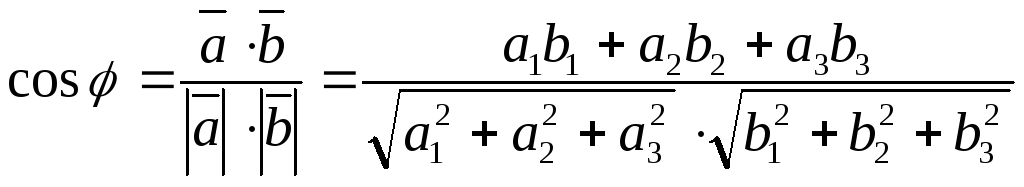
Умова колінеарності векторів.
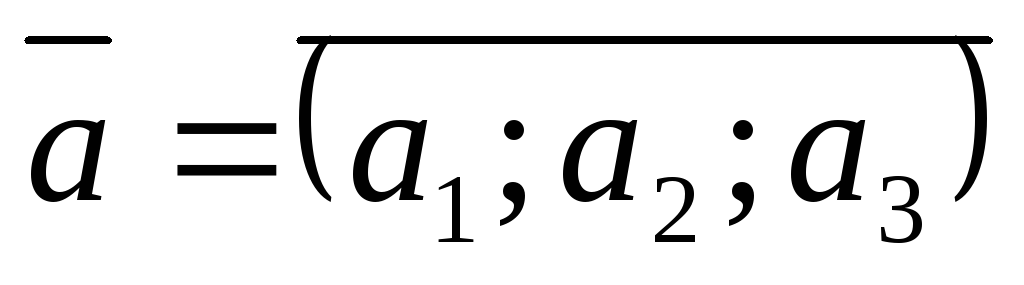 ,
,
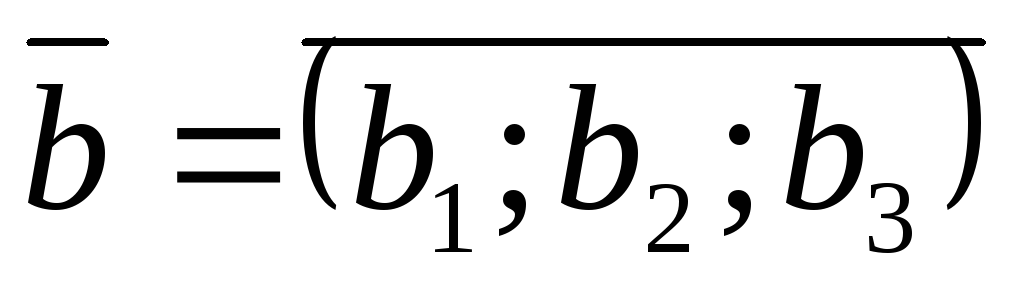
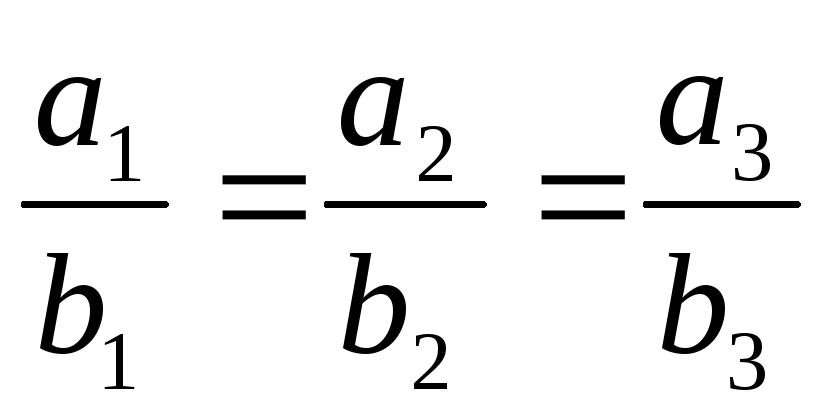 .
.Умова перпендикулярності векторів.

3. Рівняння прямої на площині».
-
№ п/п
Назва.
Рівняння.
1.
Загальне рівняння прямої.
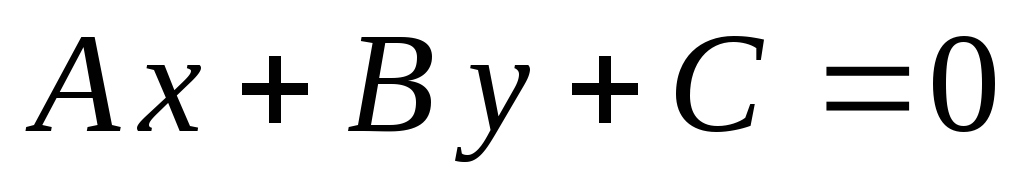
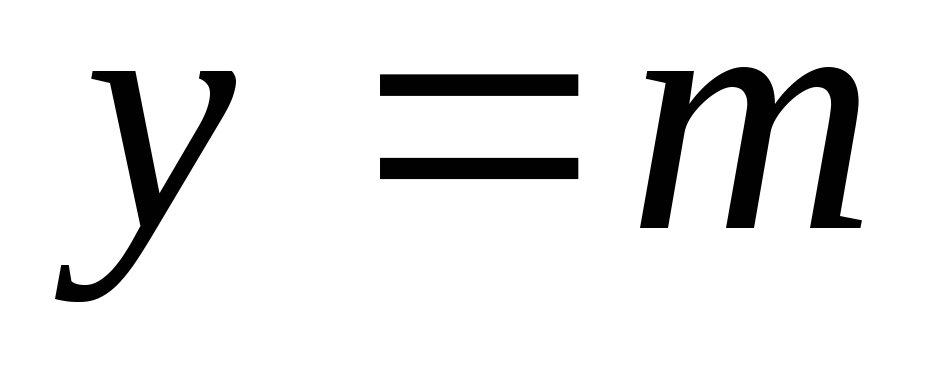
Пряма, паралельна осі Ох
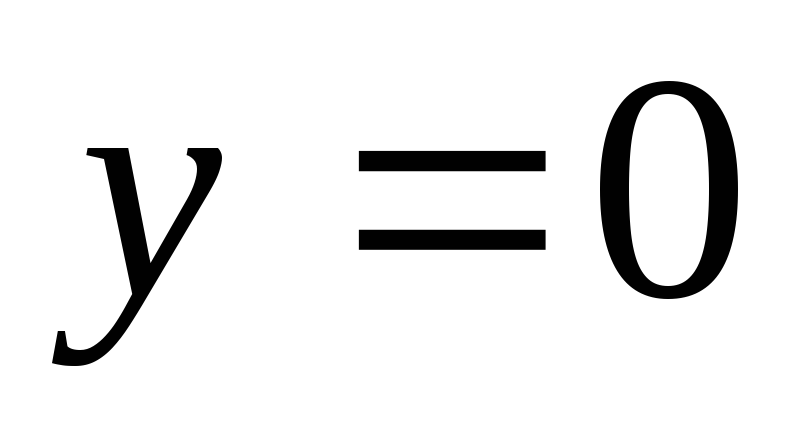
Вісь Ох
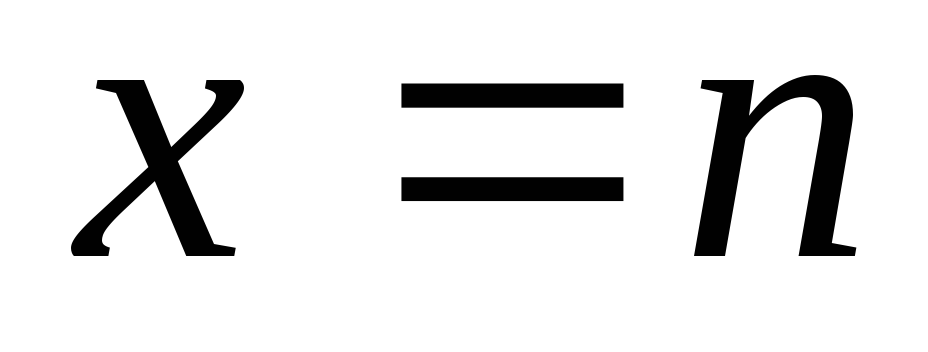
Пряма, паралельна осі Оу
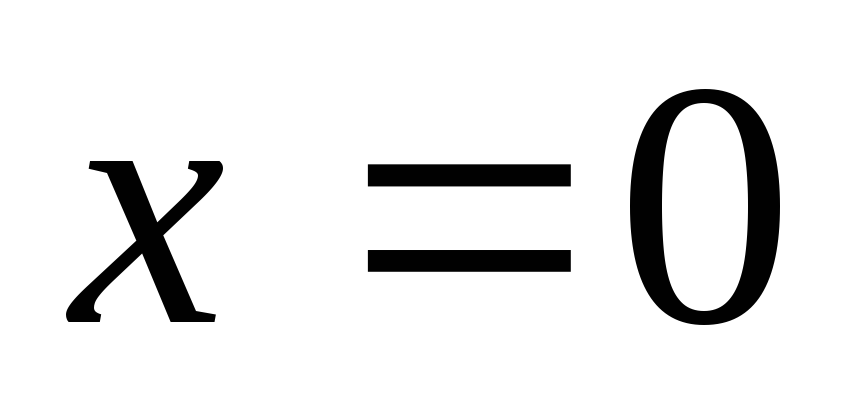
Вісь Оу
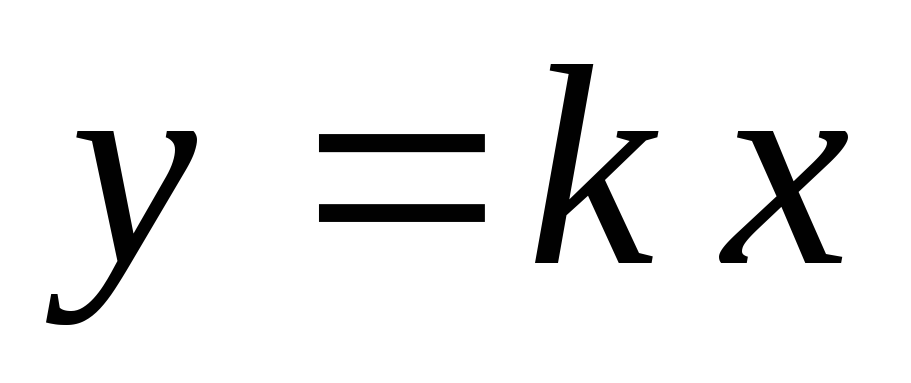
Пряма, що проходить через початок координат.
2.
Рівняння прямої у відрізках
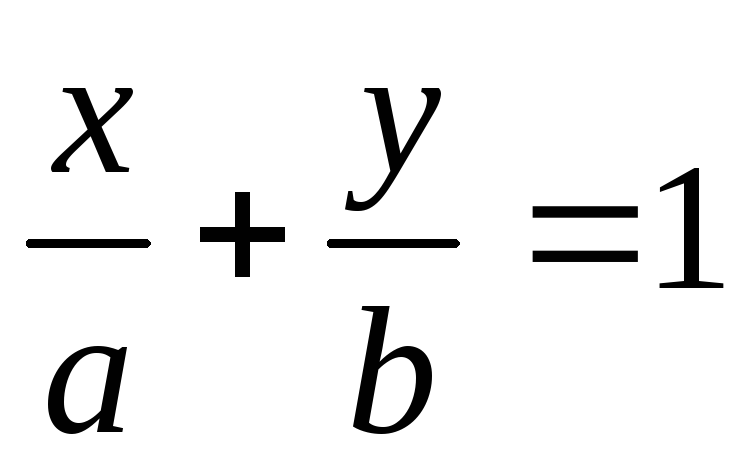
3.
Рівняння прямої з кутовим коефіцієнтом
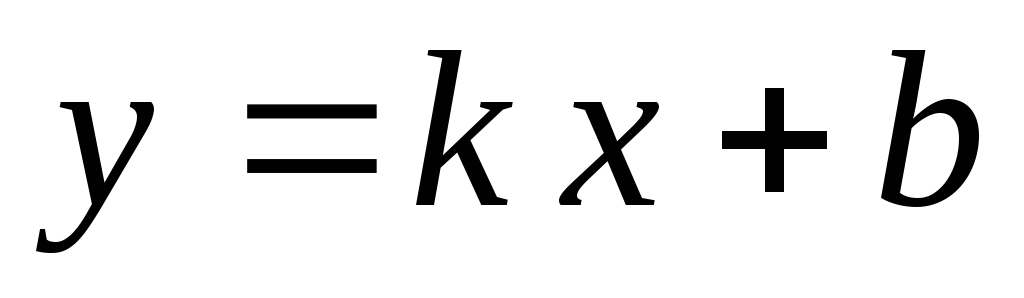 ,
,
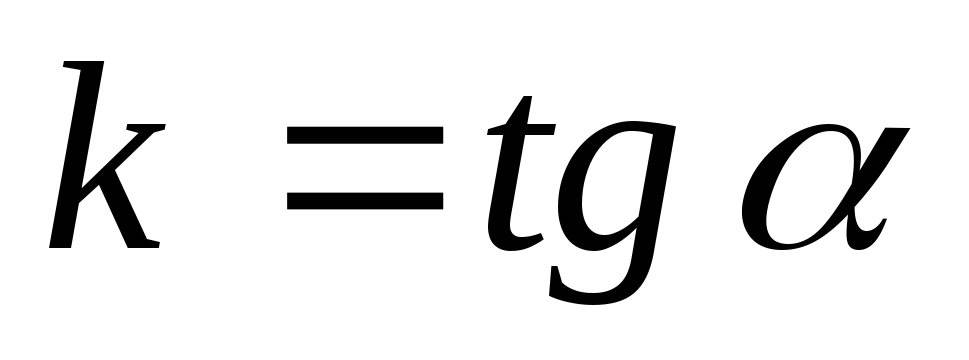 -
кутовий коефіцієнт прямої.
-
кутовий коефіцієнт прямої.4.
Рівняння прямої, що проходить через дві точки
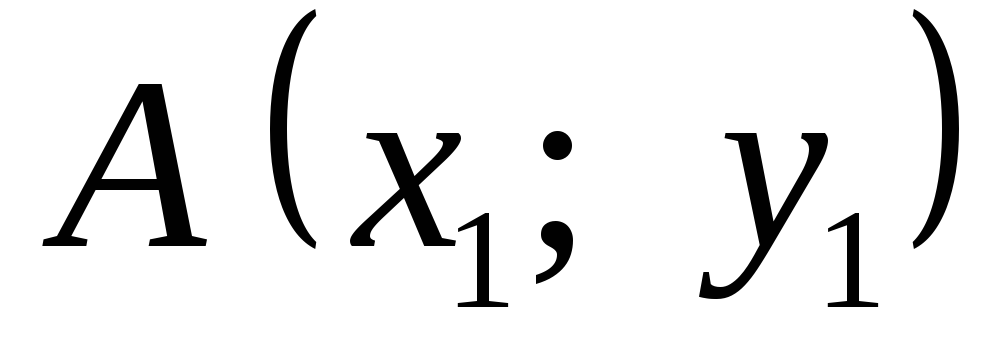 і
і
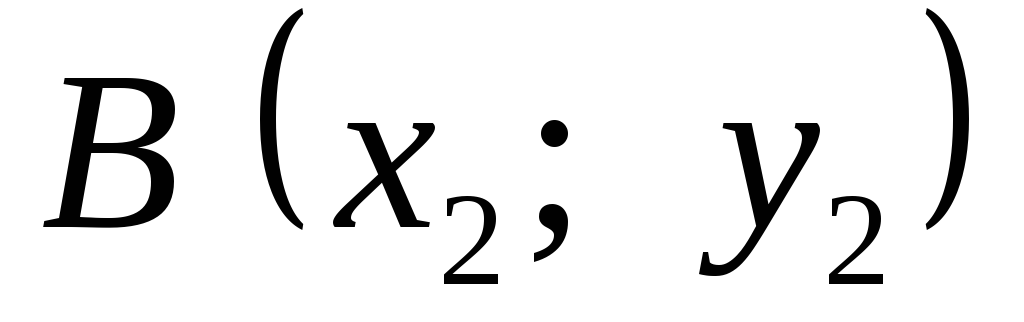
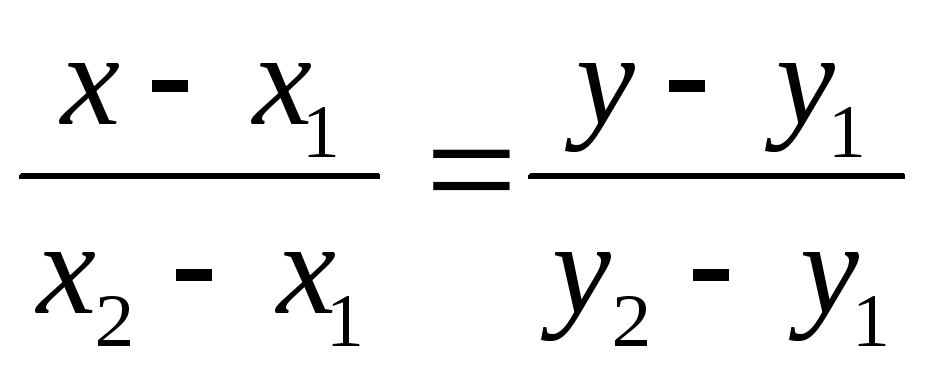
5.
Рівняння прямої з нормальним вектором
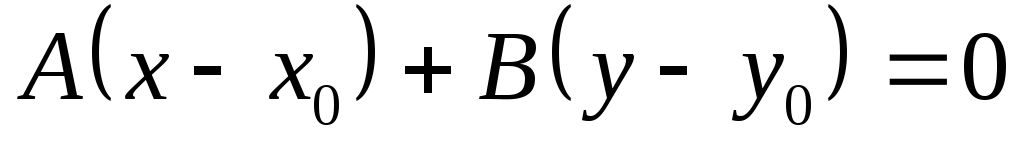
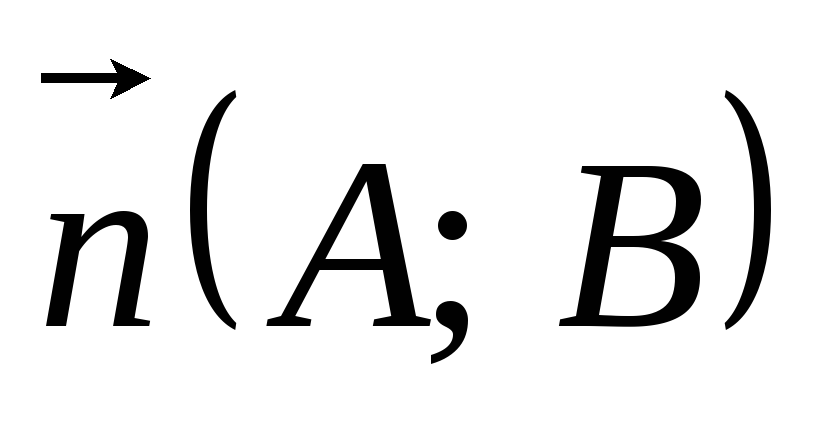 -нормальний
вектор прямої;
-нормальний
вектор прямої;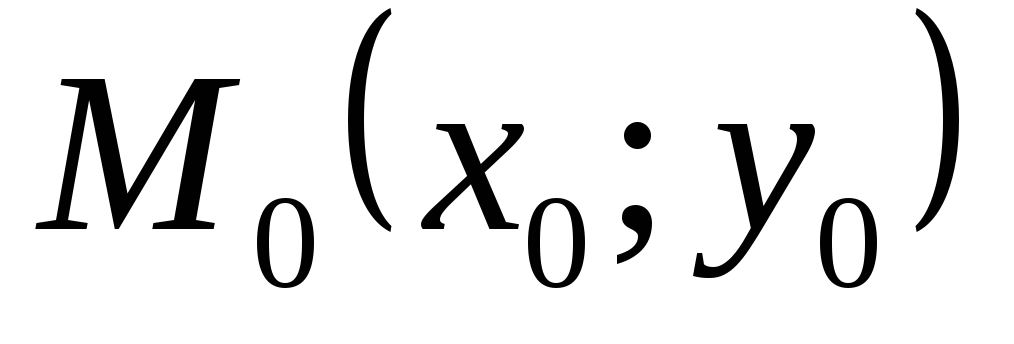 -
точка, через яку проходить пряма
-
точка, через яку проходить пряма6.
Канонічне рівняння прямої.

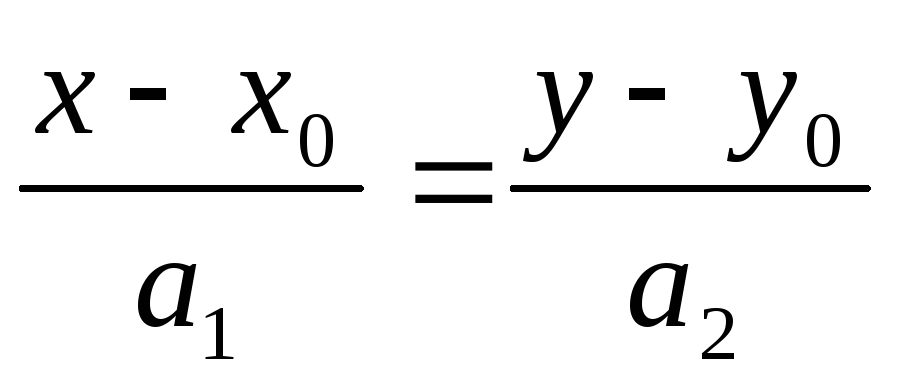
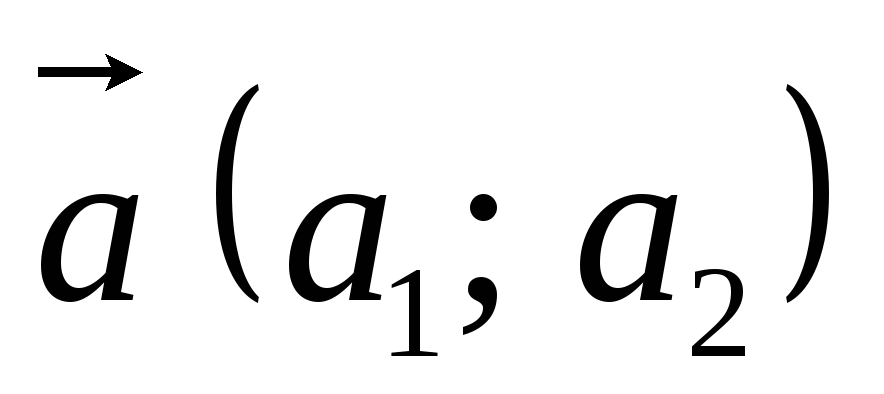 -
направляючий вектор прямої;
-
направляючий вектор прямої;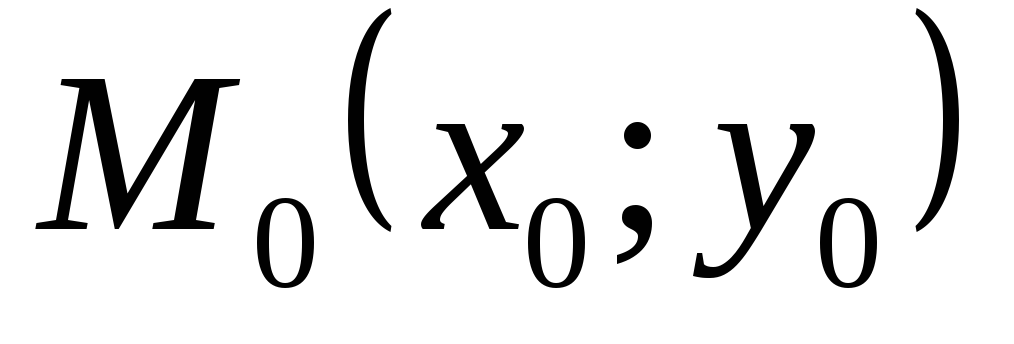 -
точка, через яку проходить пряма
-
точка, через яку проходить пряма7.
Параметричні рівняння прямої
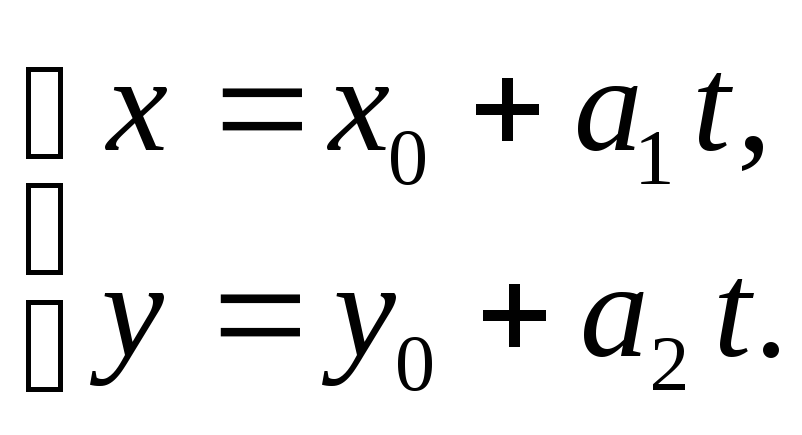
8.
Взаємне розміщення двох прямих: