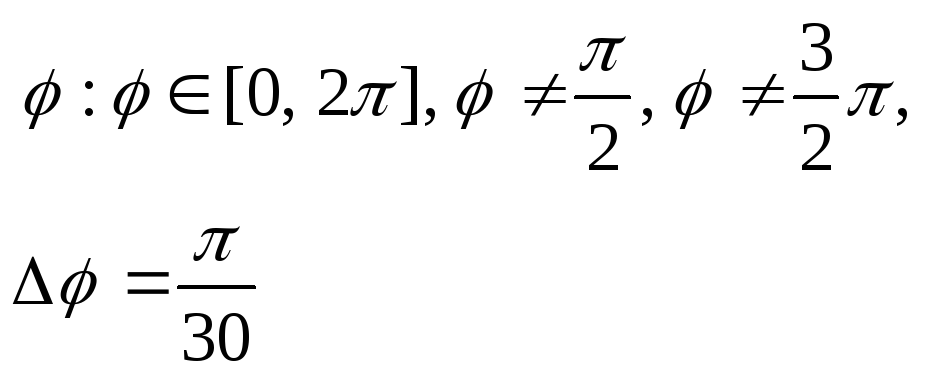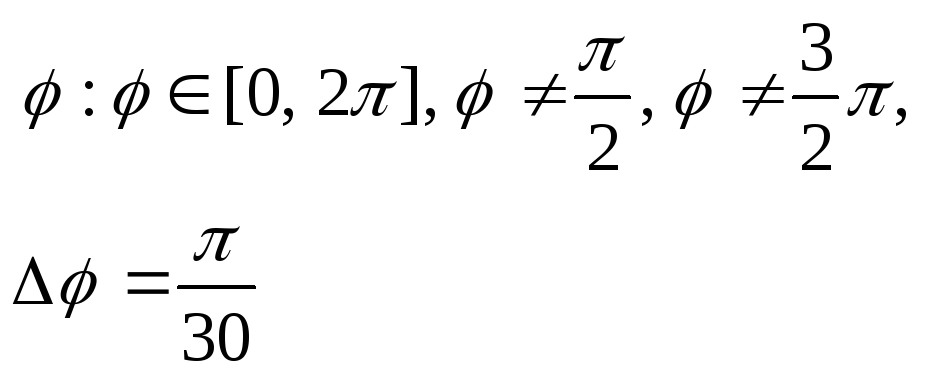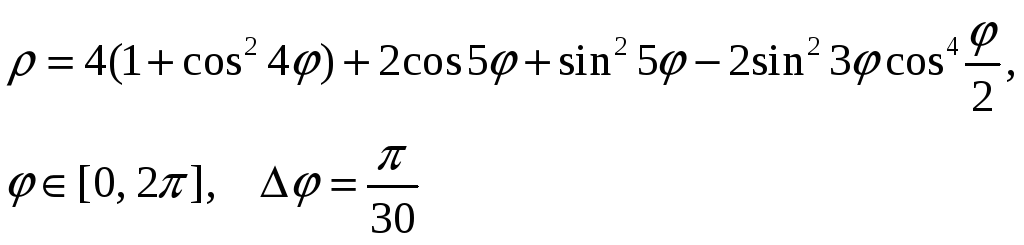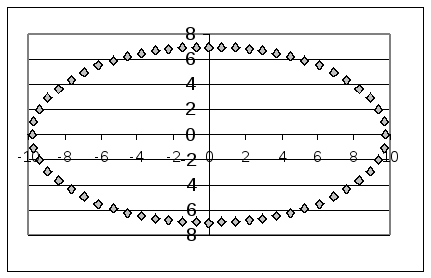
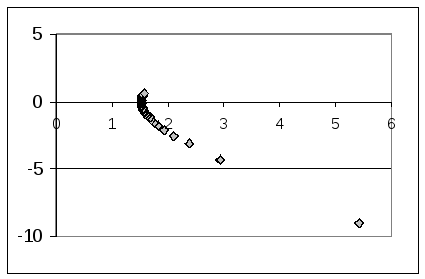
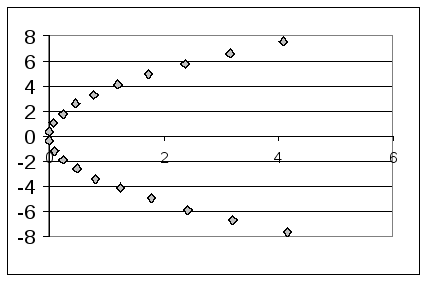
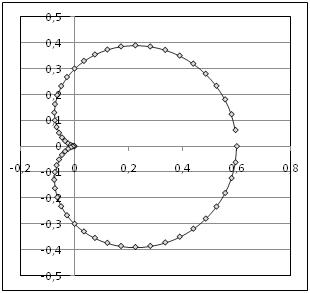
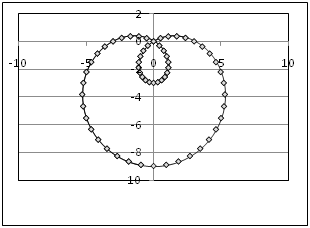
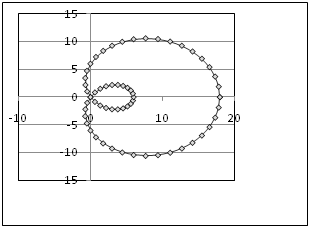
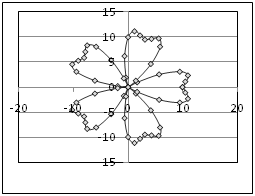
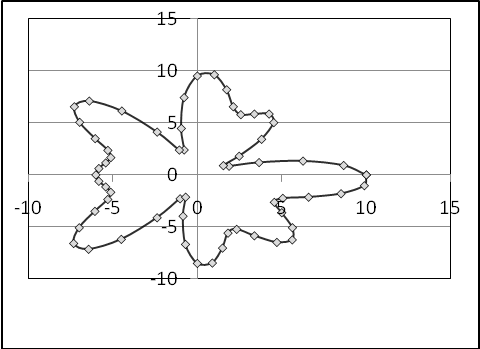
14.3. Функции, заданные уравнениями в полярных координатах

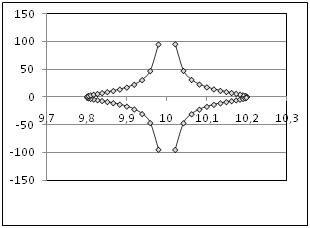
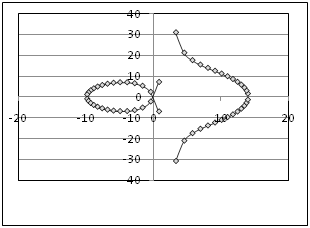
В клетке таблицы (Таблица 9) задано уравнение функции в полярных координатах r = r(j), интервал изменения параметра j и шаг изменения параметра j, он равен Dj. Табулировать функции х=x(r,j) и y=y(r,j), результаты расчетов отобразить на точечной диаграмме в плоскости X‑Y. Для проверки корректности проведенных расчетов приведена точечная диаграмма графика функции в плоскости X‑Y.

Определить параметры форматирования построенной диаграммы:

1. Для области построения диаграммы: заливка – сплошная, цвет – белый, граница – сплошная линия черного цвета.

3. Формат подписи на оси (для осей ОХ и OY): целое число, выравнивание – горизонтальное.

4. Для области построения диаграммы отобразить горизонтальные линии сетки по основной оси, отображать основные линии сетки.

5. Легенды нет.

6. Маркеры точек: тип маркера точек – встроенный, тип – ромб, размер – 7 пт, цвет линии маркера - сплошная линия черного цвета, заливка маркера – сплошная, цвет заливки маркера – «Белый. Фон 1, более темный оттенок 15%».

Таблица 9

Уравнение кривой в полярных координатах и схема точечной диаграммы этой функции в плоскости X-y

	Задание 1 ,
	Задание 2 ,
	Задание 3 ,
	Задание 4 ,
	Задание 5 ,
	Задание 6
	Задание 7
	Задание 8 , , .
	Задание 9 , , .
	Задание 10 , , .
	Задание 11
	Задание 12
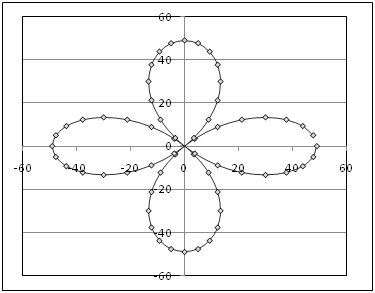
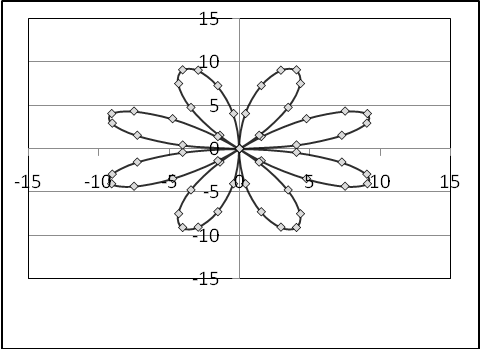
	Задание 13 Роза:
	Задание 14 Цветок:
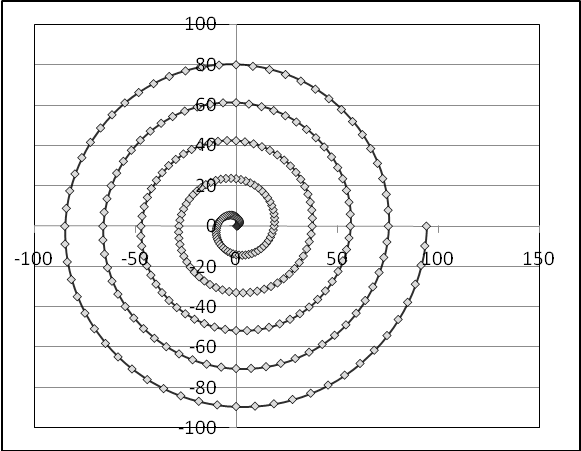
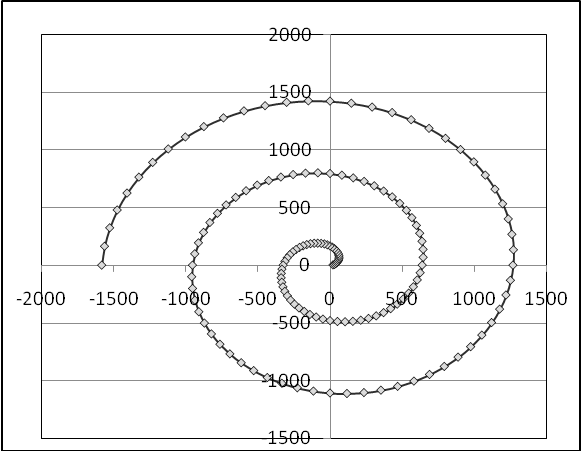
	Задание 15 Спираль Архимеда - траектория точки, равномерно движущейся по лучу, исходящему из полюса, в то время как луч равномерно вращается вокруг полюса: , , .
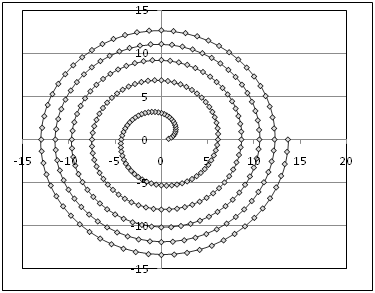
Задание 16 Траектория точки, которая движется по лучу, исходящему из полюса. В то время как луч вращается вокруг полюса. Уравнение траектории: , , .
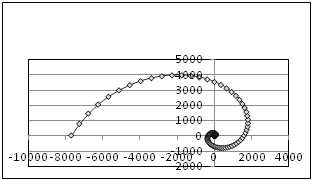
Задание 17 Параболическая спираль: , .
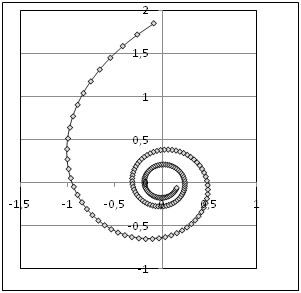
Задание 18 Логарифмическая спираль: , , .
		Задание 19 Гиперболическая спираль: , , . Замечание: при возрастании угла j до бесконечности радиус - вектор стремится к нулю, а точка кривой стремится к совпадению с полюсом, никогда его не достигая. Кривая бесчисленное множество раз заворачивается вокруг полюса.