Системы линейных однородных уравнений

Если в системе линейных алгебраических уравнений все свободные члены равны нулю,

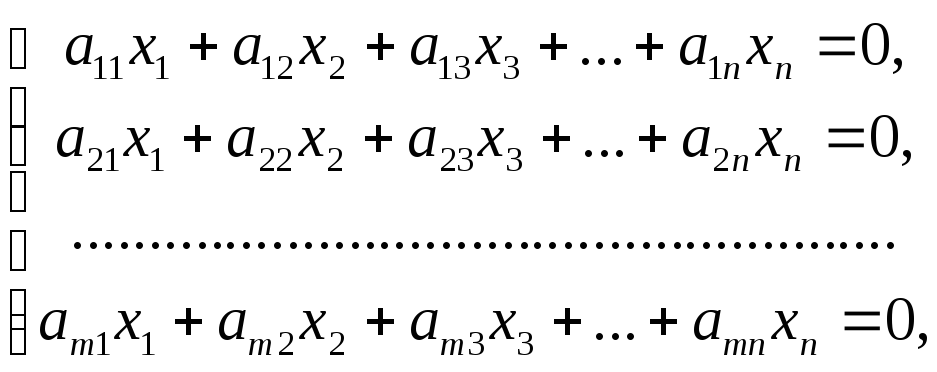( 20 )

она называется системой линейных однородных уравнений, или однородной системой линейных уравнений.

Матрица системы и расширенная матрица

системы линейных однородных уравнений (20) имеют одинаковые ранги (почему?). Следовательно, такая система всегда совместна, например, она имеет нулевое (очевидное, или тривиальное) решение

.

Отсюда возникает основной вопрос: при каких условиях система (20) имеет ненулевые решения.

Пусть , и - базисный минор матрицы А (напомним, что таких миноров может быть несколько, и мы можем взять любой из них). Оставляя только базисные уравнения и отбрасывая небазисные, мы получаем систему уравнений с n неизвестными.

Если количество неизвестных n = k, система имеет только тривиальное решение, так как ее главный определитель отличен от нуля, а все вспомогательные определители равны нулю.

Если n > k, система имеет свободных неизвестных, а следовательно - бесконечное множество решений. Можно получить ее общее решение уже изложенным выше методом. Но факт однородности системы позволяет пойти немного дальше, основываясь на свойствах ее решений. Именно,

а) если - решение системы (20), то его произведение на любое число , то есть , также является решением;

б) если - два решения системы (20), то их сумма, то есть , также является решением.

Попробуйте доказать эти два свойства самостоятельльно.

Названные свойства решений лежат в основе теоремы, согласно которой все решения системы линейных однородных уравнений (20) могут быть получены из так называемой фундаментальной системы решений. Последнюю можно создать, последовательно приписывая значения

свободным неизвестным, входящим в общее решение системы.

Пример. Найти фундаментальную систему решений следующей системы линейных однородных уравнений:

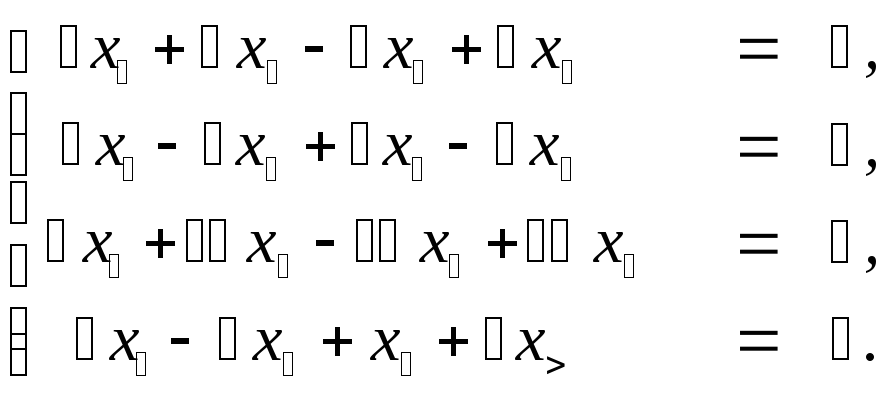
Матрица системы

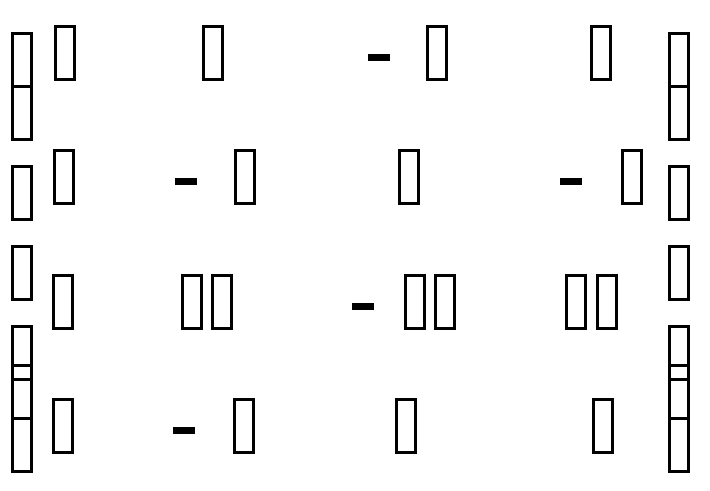
имеет ранг k = 2 (проверьте!), в качестве базисного минора мы можем выбрать следующий

,

так что базисными уравнениями и неизвестными являются первые два. Мы отбрасываем третье и четвертое уравнения и переносим свободные неизвестные направо,

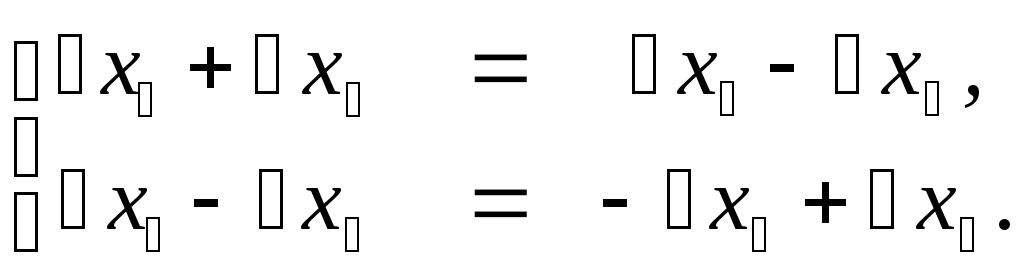
Общее решение системы имеет вид (проверьте!)

.

Полагая последовательно в общем решении, мы получаем фундаментальную систему решений, а именно:

,

или (умножая оба ее решения на 17)

.

Собственные значения и собственные векторы матрицы

Пусть M – множество всех n-мерных векторов-столбцов, а именно множество всех матриц-столбцов размера , и отображение f множества M в себя, определенное квадратной матрицей n-го порядка

.

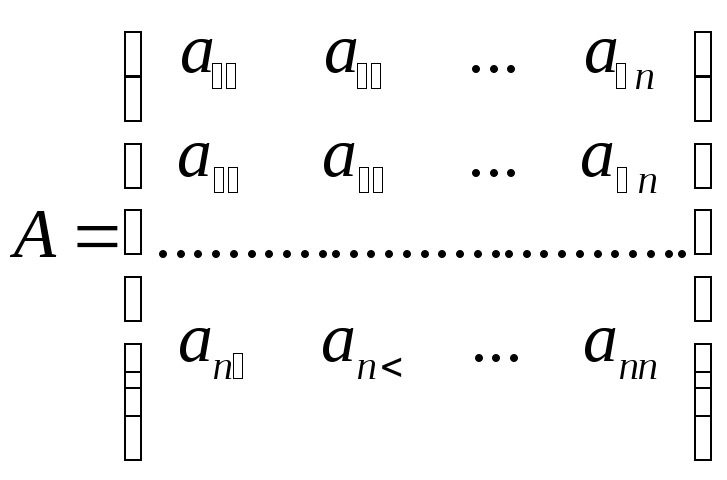Это означает что каждому вектору

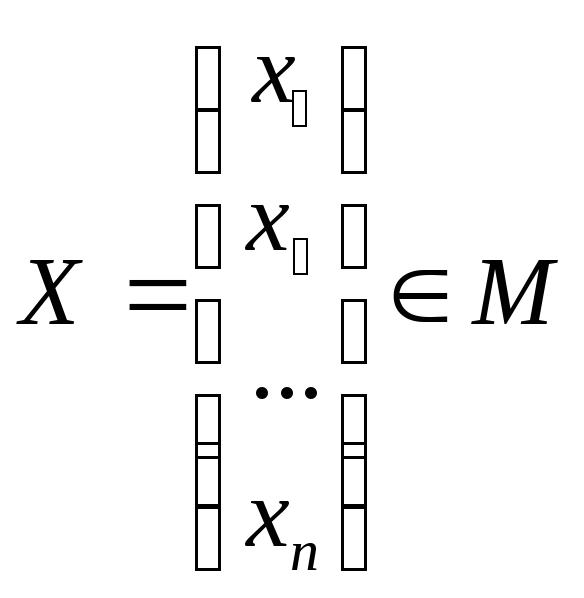
матрица А ставит в соответствие единственный вектор

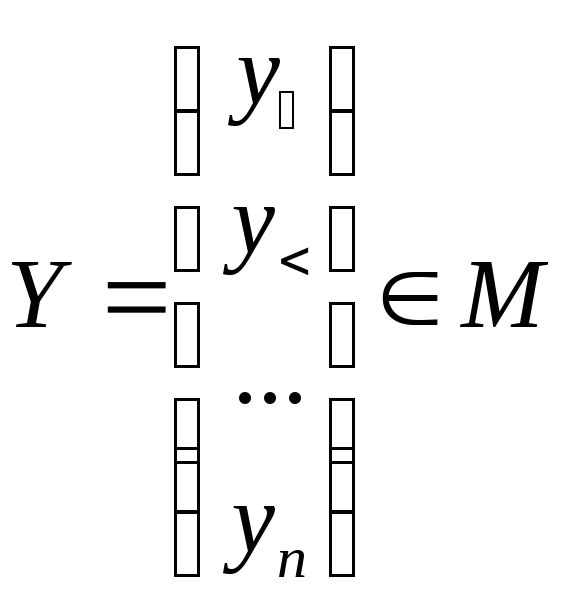
такой, что

. ( 21 )

Во многих приложениях, в том числе экономических, часто возникает следующий вопрос: существует ли ненулевой вектор X (собственный вектор), для которого

, ( 22 )

где - некоторое число (собственное значение)?

1. Известно, что собственные значения находятся как корни следующего уравнения

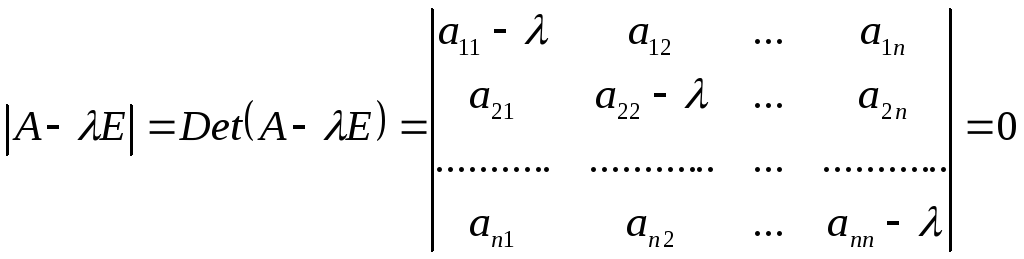. ( 23 )

Последнее (после раскрытия определителя) является алгебраическим уравнением n-ой степени относительно .

2. Для каждого корня уравнения (23) (то есть для каждого собственного значения) один или несколько соответствующих собственных векторов находят, решая следующее матричное уравнение

,

или (в развернутом виде)

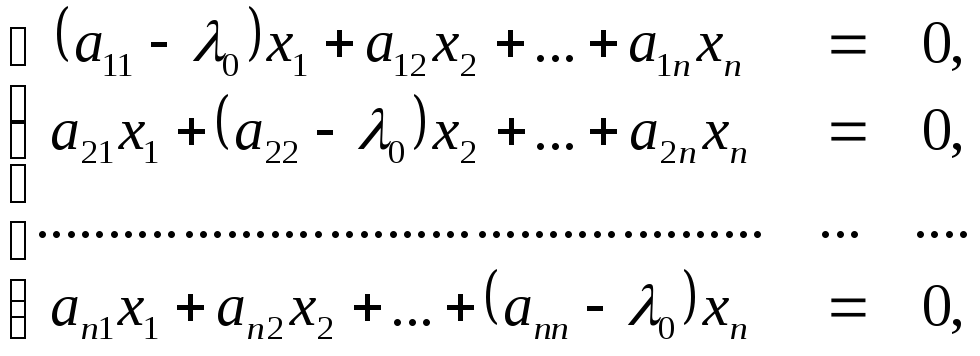( 24 )

- систему линейных однородных уравнений относительно . На основании (23) ранг ее матрицы меньше n.

Пример. Найти собственные значения и собственные векторы матрицы третьего порядка

.

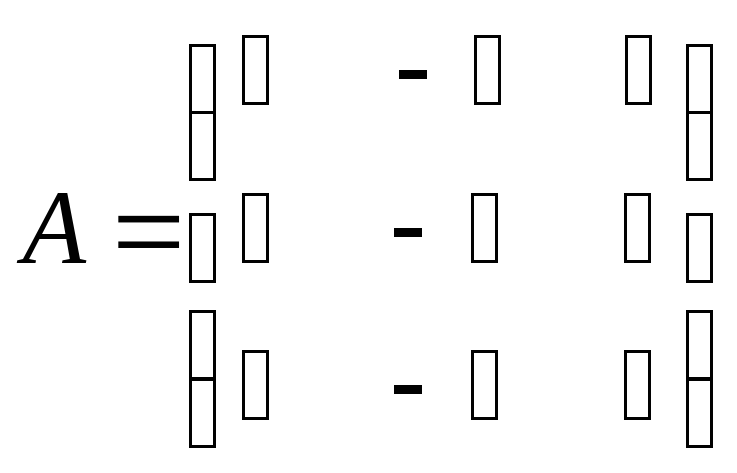Шаг 1. Находим собственные значения матрицы А. На основании формулы (23) мы должны решить уравнение

.

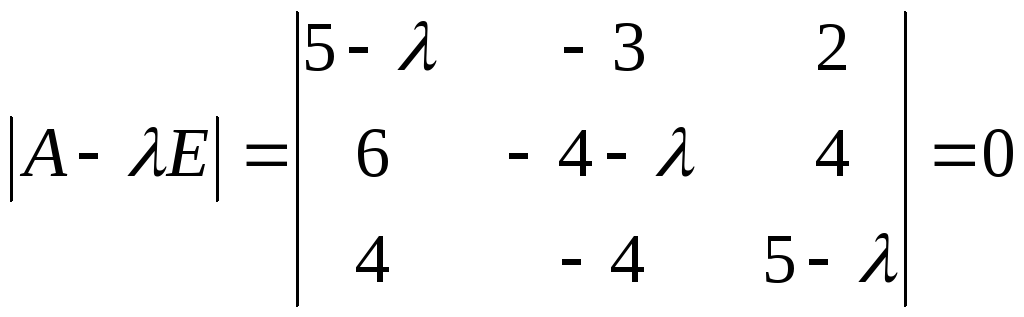Раскрывая определитель, имеем

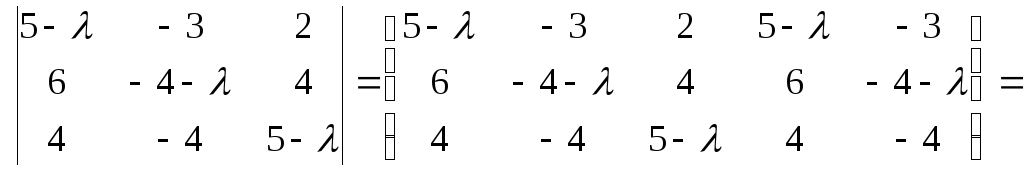
Полученное кубическое уравнение имеет три различных корня

Шаг 2.1. Для мы на основании (24) должны решить следующую систему линейных однородных уравнений

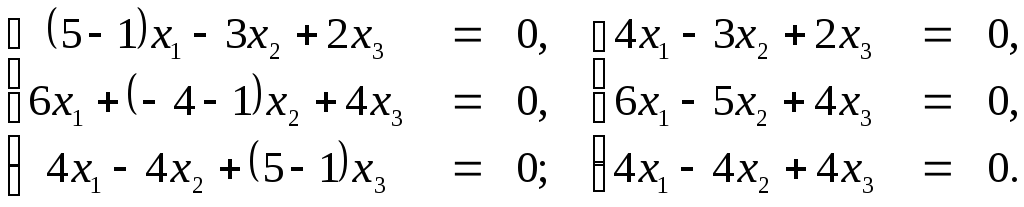
Матрица системы

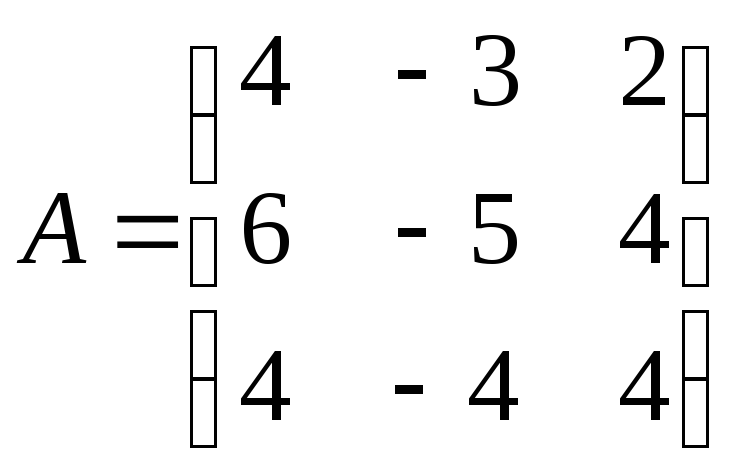
имеет ранг 2, так как ее определитель (он же единственный минор 3-го порядка) равен нулю, а, например, минор 2-го порядка

отличен от нуля. Взяв этот минор в качестве базисного, мы определяем первое и третье уравнения, первые два неизвестных как базисные, а третье неизвестное как свободное, откуда

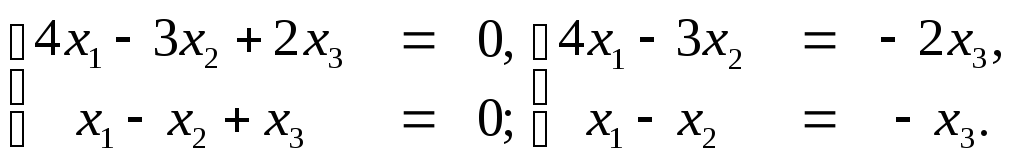
Полагая , мы находим значения и собственный вектор, соответствующий собственному значению , а именно

.

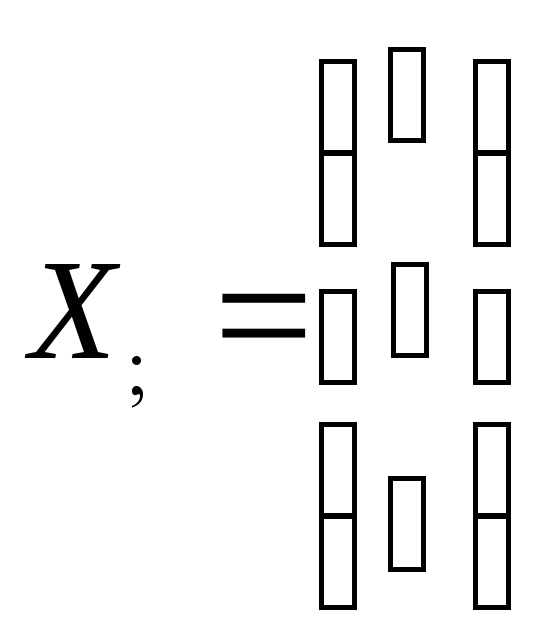Шаг 2.2. Для мы аналогично имеем

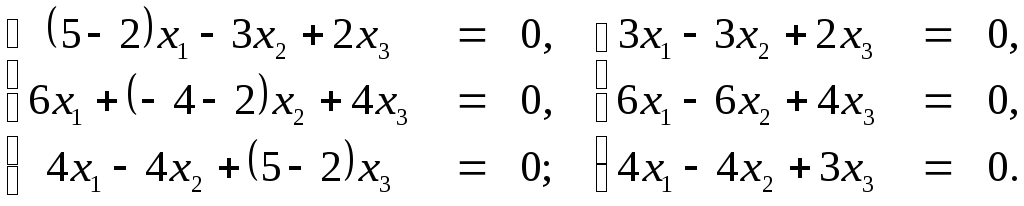
Базисными уравнениями и неизвестными здесь являются первые и третьи, а свободным неизвестным - . Следовательно,

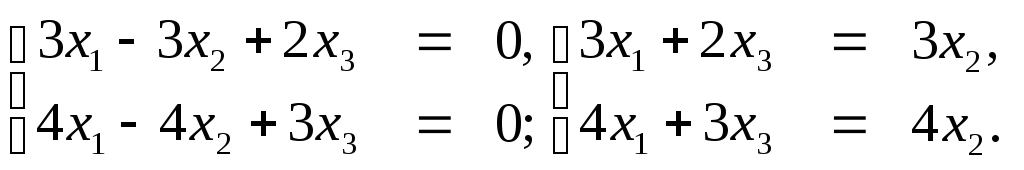
Полагая , получаем и второй собственный вектор

.

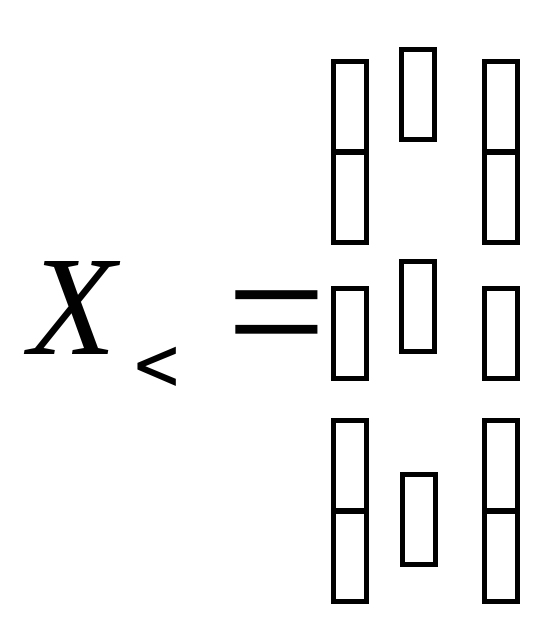Шаг 2.3. Наконец, для мы таким же образом получаем третий собственный вектор

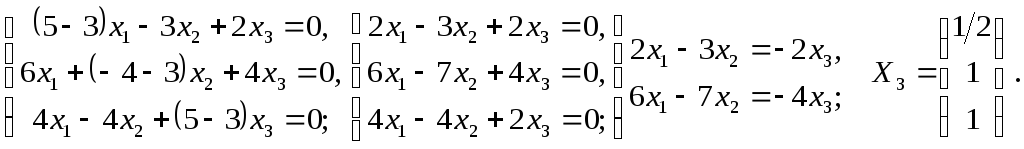
Ответ: собственные векторы, соответствующие собственным значениям , соответственно равны

, ,
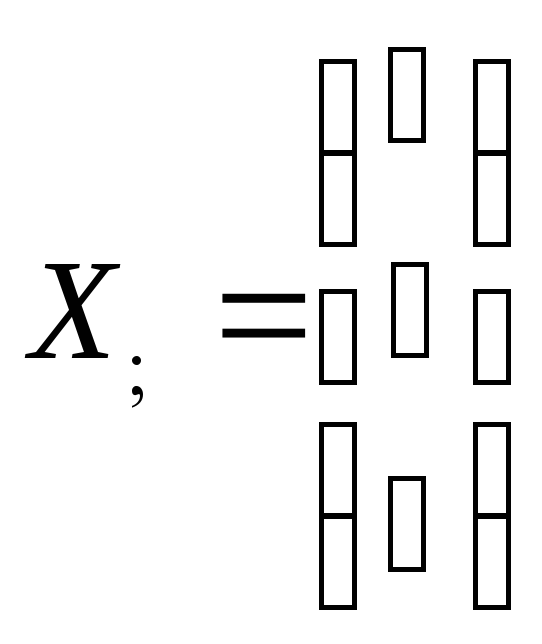
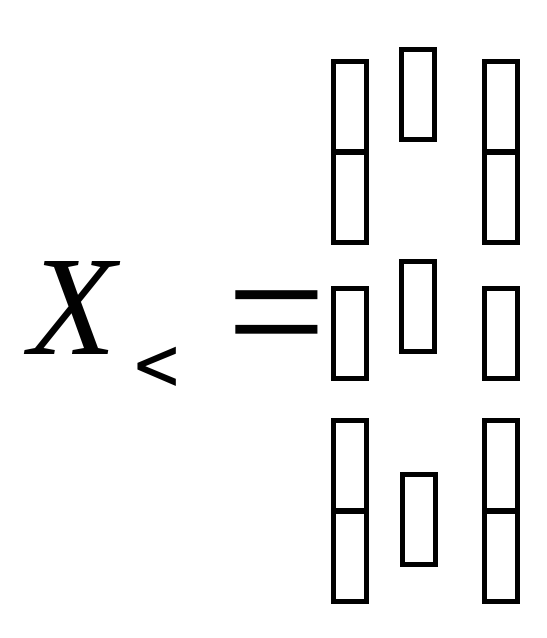