
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
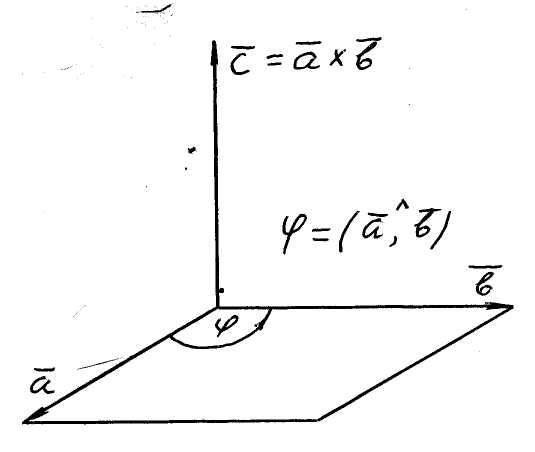
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Векторное произведение двух векторов
|
|
|
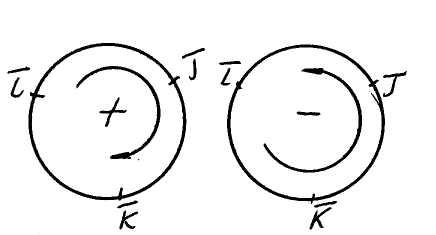
Рис. 5 Рис. 6 ра происходящим против часовой стрелки (см. рис. 5).
Направление третьего вектора правой тройки можно определить по правилу правой руки, если считать большой, указательный и средний ее пальцы соответственно первым, вторым и третьим векторами.
В дальнейшем мы будем рассматривать
только правый декартовый ортонормированный
базис
![]() и соответствующую правую декартову
прямоуголь-ную систему координат (рис.
6). Очевидно, что для правого базиса
и соответствующую правую декартову
прямоуголь-ную систему координат (рис.
6). Очевидно, что для правого базиса
![]() упорядоченные тройки векторов
упорядоченные тройки векторов
![]() и
и
![]() также являются правыми.
также являются правыми.
 Векторным
произведением
Векторным
произведением
![]() векторов
векторов
![]() и
и
![]() называется вектор: а) перпендикулярный
векторам
называется вектор: а) перпендикулярный
векторам
![]() и
и
![]() ;
б) имеющий длину (модуль), равный
произведению длин векторов
;
б) имеющий длину (модуль), равный
произведению длин векторов
![]() и
и
![]() на синус угла между ними;
в) образующий
с векторами
на синус угла между ними;
в) образующий
с векторами
![]() и
и
![]() правую тройку
Рис. 7
векторов, а именно
правую тройку
Рис. 7
векторов, а именно
![]() ,
,
![]() ,
,
![]() .
.
Пример. Векторные произведения векторов правого декартового ортонормированного базиса (см. cхему на рис. 7)
![]() .
( 20 )
.
( 20 )
В самом деле, вектор
![]() перпендикулярен векторам
перпендикулярен векторам
![]() ,
его длина действительно равна
,
его длина действительно равна
![]() ,
а векторы
,
а векторы
![]() обра-зуют правую тройку. Поэтому
обра-зуют правую тройку. Поэтому
![]() .
.
 Аналогично
доказывается справедливость остальных
векторных произведений формулы (20).
Аналогично
доказывается справедливость остальных
векторных произведений формулы (20).
Длина (модуль)
![]() векторного
произведения
векторного
произведения
![]() имеет простой геометрический смысл:
она численно рав-на площади параллелограмма,
построенного на векторах
имеет простой геометрический смысл:
она численно рав-на площади параллелограмма,
построенного на векторах
![]() Рис. 8 и
Рис. 8 и
![]() как на сторонах (рис. 8),
как на сторонах (рис. 8),
![]() .
( 21 )
.
( 21 )
Необходимо запомнить свойства векторного
произведения: 1) антиперестановочность
(![]() ),
2) сочетательность относительно скалярного
(в том числе числового) множителя
),
2) сочетательность относительно скалярного
(в том числе числового) множителя
![]() ,
3) распределительность относительно
векторных сомножителей
,
3) распределительность относительно
векторных сомножителей
![]()
![]() .
Отметим еще одно свойство:
.
Отметим еще одно свойство:
4) Два ненулевых вектора коллинеарны тогда и только тогда, если их векторное произведение равно нулевому вектору.
Если векторы заданы в правом
декартовом ортонормированном базисе
![]() ,
то есть если
,
то есть если
![]() ,
,
или просто
![]() ,
,
то их векторное произведение выражается
определителем третьего порядка, в первой
строке которого находятся базисные
векторы
![]() ,
во второй - координаты первого сомножителя,
в третьей – координаты второго,
,
во второй - координаты первого сомножителя,
в третьей – координаты второго,
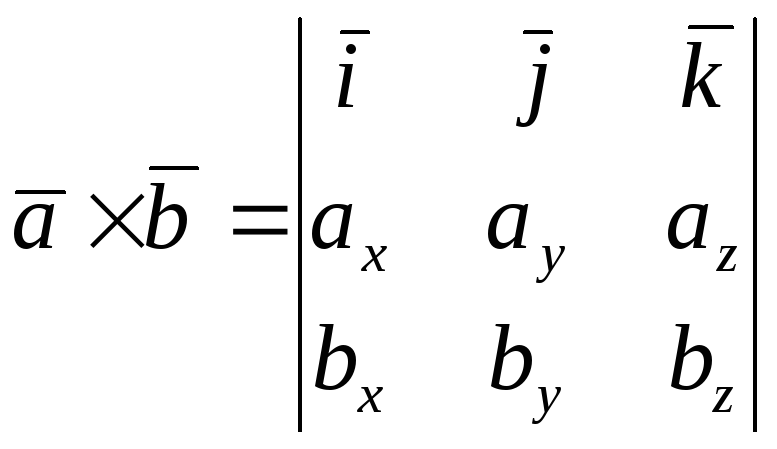 .
( 22 )
.
( 22 )
Разложив определитель третьего порядка по элементам первой строки, получим еще одно представление векторного произведения, именно:
![]() ,
,
где
![]() -
алгебраические дополнения элементов
первой строки определителя (22) и их
выражения через миноры этих же элементов.
-
алгебраические дополнения элементов
первой строки определителя (22) и их
выражения через миноры этих же элементов.
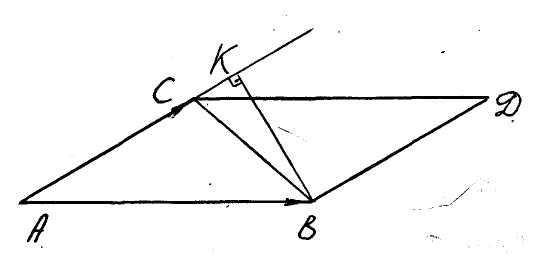 Пример.
Найти площадь и высоту BK,
проведен-ную из вершины B,
треугольника с заданными верши-нами
A(1; 3; 5), B(2;
-4; 6), C(0; -2; 3) (рис. 9).
Пример.
Найти площадь и высоту BK,
проведен-ную из вершины B,
треугольника с заданными верши-нами
A(1; 3; 5), B(2;
-4; 6), C(0; -2; 3) (рис. 9).
Пусть
![]() ,
,![]() .
Пло-
Рис. 9 щадь
треугольника ABC равна
половине площади параллелограмма ABDC,
построенного на векторах
.
Пло-
Рис. 9 щадь
треугольника ABC равна
половине площади параллелограмма ABDC,
построенного на векторах
![]() как на сторонах. Последняя на основании
формулы (21) равна
как на сторонах. Последняя на основании
формулы (21) равна
![]() ,
,
и поэтому
![]() .
.
Для отыскания высоты BK примем во внимание известную из школы формулу площади треугольника. Именно,
![]()
По формуле (22)
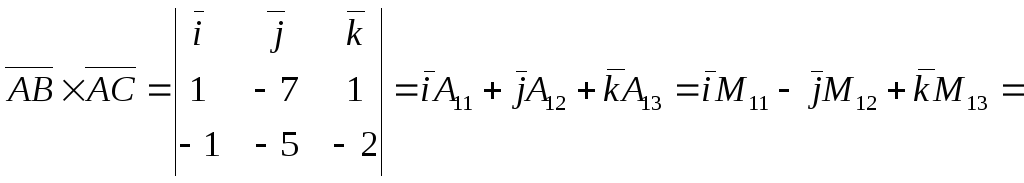
![]()
![]()
Следовательно,
![]() .
.
Пример. Найти вектор длины 14, если он
перпендикулярен двум данным векторам
![]() и образует острый угол с осью Oz.
и образует острый угол с осью Oz.
Искомый вектор
![]() ,
будучи перпендикулярным к векторам
,
будучи перпендикулярным к векторам
![]() ,
коллине-арен их векторному произведению
,
коллине-арен их векторному произведению
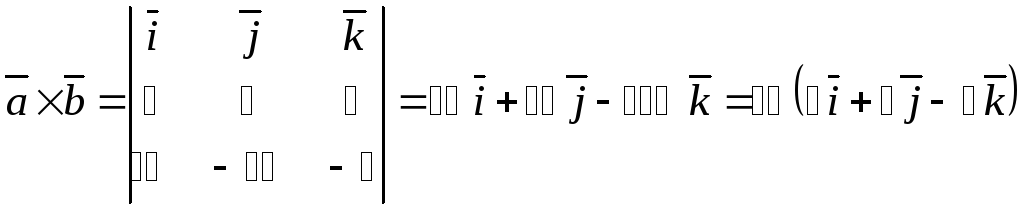 ,
,
или более простому вектору
![]() .
.
Последний образует тупой угол с осью
Oz (так его
z-координата
отрицатель-ная), поэтому орты векторов
![]() и
и
![]() должны
быть противоположными, и
должны
быть противоположными, и
![]() .
.
Окончательно получаем
![]() .
.
Пример. Найти вектор
![]() ,
перпендикулярный двум векторам
,
перпендикулярный двум векторам
![]()
![]() ,
если его проекция на вектор
,
если его проекция на вектор
![]() равна
равна![]() .
.
Аналогично предыдущему примеру искомый
вектор
![]() должен быть коллинеарным векторному
произведению
должен быть коллинеарным векторному
произведению
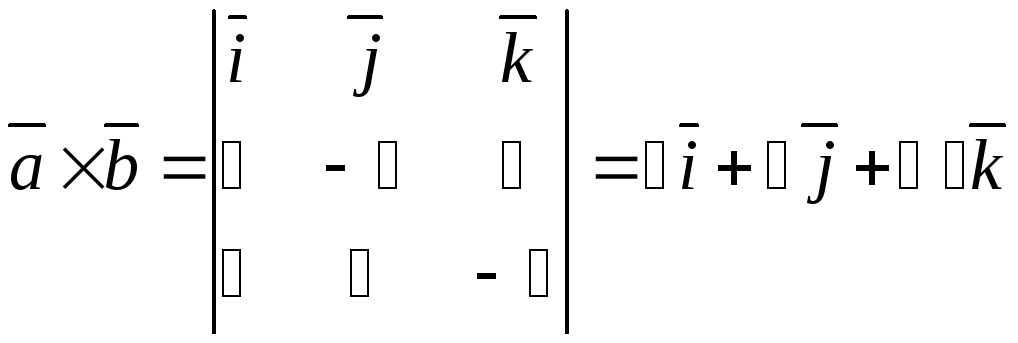
и поэтому должен иметь вид
![]() ,
,
где
![]() - некоторое неизвестное число. По условию
(см. еще формулу (17))
- некоторое неизвестное число. По условию
(см. еще формулу (17))
![]() ,
,
следовательно
![]() .
.

 Fig.
2
Fig.
2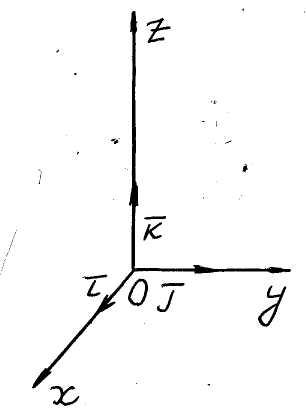 Fig.
3
Fig.
3