2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Косолапов Ю.Ф.

ЛИНЕЙНАЯ АЛГЕБРА АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Учебное пособие для изучения разделов курса высшей математики первого семестра

Рассмотрено на заседании кафедры высшей математики Протокол № 2 от 08 октября 2008 г.

Утверждено на заседании учебно-издательского совета ДонНТУ протокол № 1 от 11 марта 2009 г.

Донецк 2009

УДК 512+514+517(071)

Косолапов Ю.Ф. Линейная алгебра и аналитическая геометрия: Учебное пособие для изучения разделов курса высшей математики первого семестра / - Донецк: РВА ДонНТУ, 2009. – 113 с.

Содержат указания к выполнению индивидуальных заданий по темам: "Определители", "Матрицы", "Системы линейных уравнений", "Векторная алгебра", "Ана­литическая геометрия на плоскости", "Аналитическая геометрия в пространстве". Тщательно рассматриваются примеры решения типичных задач. Приведены вопросы для самопроверки, теоретические упражнения, дополнительные задачи повышенной трудности.

Для студентов и преподавателей технических вузов.

СОСТАВИТЕЛЬ: Косолапов Ю.Ф.

РЕЦЕНЗЕНТ: кандидат физико-математичних наук, доцент Косилова Е.Ф.

ОТВЕТСТВЕННЫЙ ЗА ВЫПУСК: зав. кафедрой высшей математики ДонНТУ, доктор технических наук, профессор Улитин Г.М.

Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители

Как известно, определитель второго порядка определяется следующим равенством:

. ( 1 )

Например,

Определитель третьего порядка определяется следующим равенством:

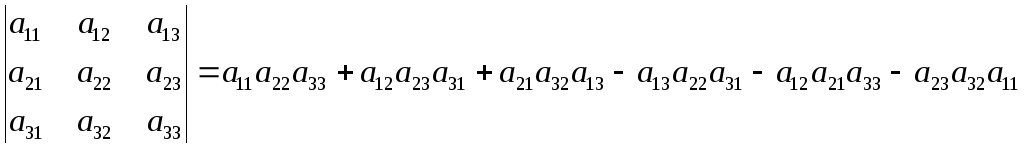. ( 2 )

Существует несколько способов запомнить правую часть этого равенства. Один из них дается следующей схемой:

«+» «-»

a₁₁ a₁₂ a₁₃ a₁₁ a₁₂ a₁₁ a₁₂ a₁₃ a₁₁ a₁₂

a₂₁ a₂₂ a₂₃ a₂₁ a₂₂ a₂₁ a₂₂ a₂₃ a₂₁ a₂₂

a₃₁ a₃₂ a₃₃ a₃₁ a₃₂ a₃₁ a₃₂ a₃₃ a₃₁ a₃₂

Хорошо известен другой способ – так называемое правило Сайрюса.

Пример. Вычислить определитель третьего порядка

.

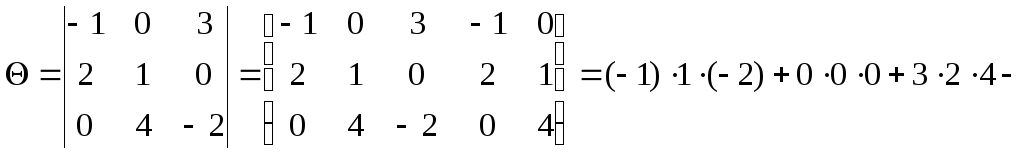
Минором элемента определителя называется определитель, получающийся из данного вычеркиванием i-ой строки и j-го столбца.

Пример. Миноры всех элементов вычисленного выше определителя

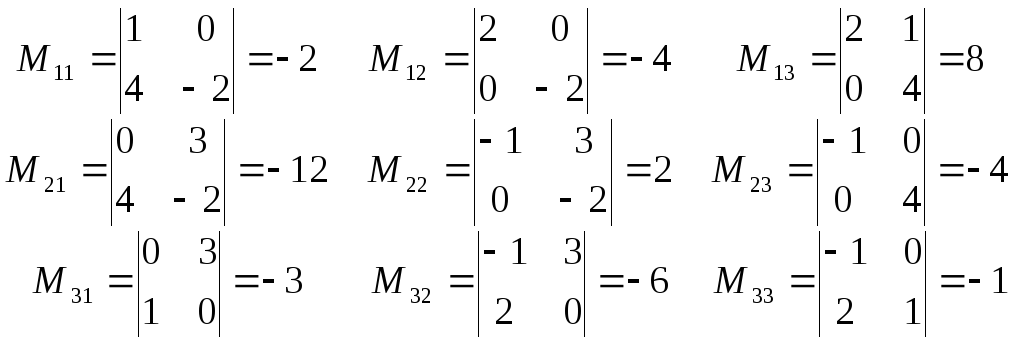
Алгебраическим дополнением элемента определителя называется минор этого элемента, взятый со знаком , то есть с тем же самым знаком, если сумма является четным числом, и с противоположным знаком в противном случае:

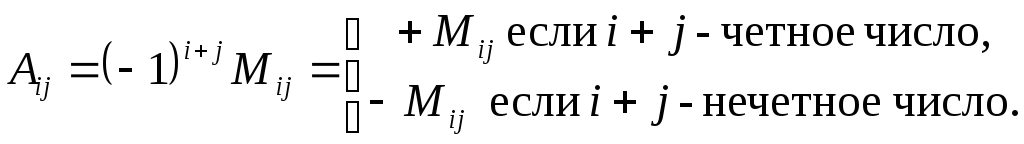
Пример. Алгебраические дополнения всех элементов уже рассмотренного определителя суть

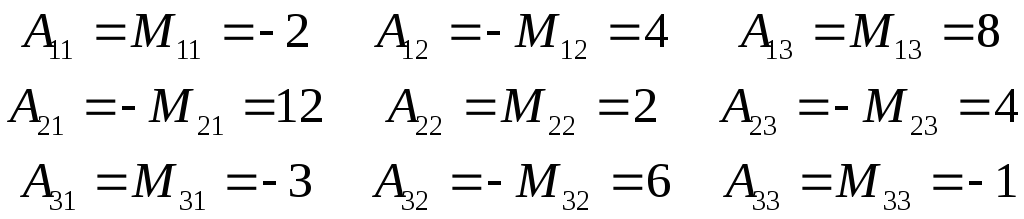
Студент должен знать свойства определителей, которые можно найти в любом пособии по линейной алгебре.

Вычисление определителей четвертого, пятого, … порядков сводится к вычислению определителей соответственно третьего, четвертого, … порядков с помощью свойства о разложении определителя по элементам строки или столбца (определитель равен сумме произведений всех элементов любой его строки или любого его столбца на алгебраические дополнения этих же элементов). Полезным вспомогательным средством является следующее свойство определителя (так называемое свойство - создатель нулей): определитель не изменится, если к элементам любой его строки (любого его столбца) прибавить соответствующие элементы другой строки (соответственно другого столбца), предварительно умноженные на какое-либо число. С помощью последнего свойства в каком-нибудь ряде (строке или столбце) определителя создают максимально возможное количество нулей, а затем раскладывают определитель по этому ряду (строке или столбцу).

Пример. Вычислить определитель четвертого порядка

.

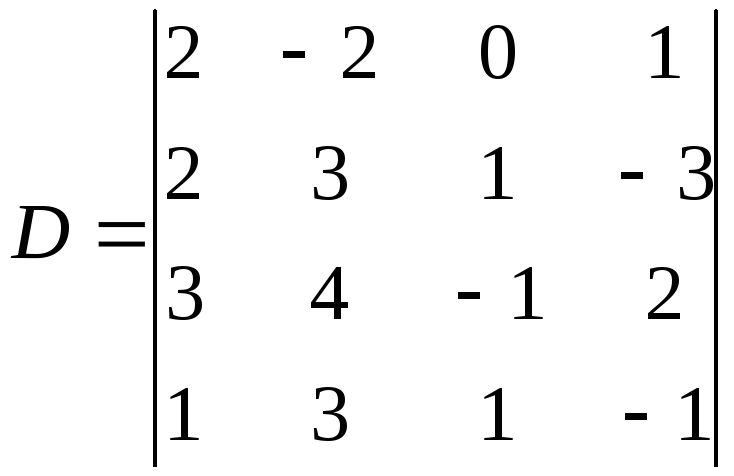Первый шаг. Первая строка определителя уже содержит один нуль. Образуем в ней еще два нуля. Например, прибавим элементы четвертого столбца, предварительно умноженные на , к соответственным элементам первого столбца, а предварительно умноженные на , - к соответственным элементам второго столбца. Так как данный определитель при этом не изменяется, то мы получаем

.

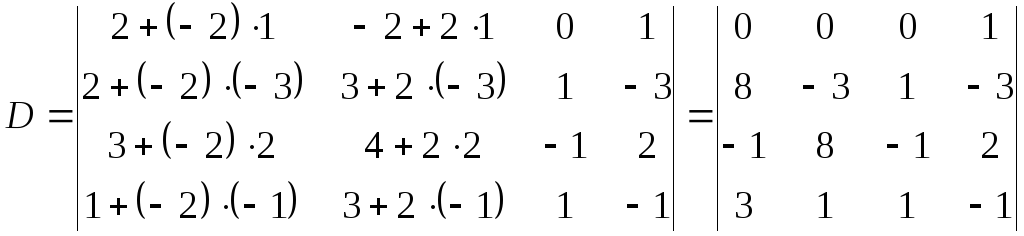Второй шаг. Разложим полученный определитель по элементам первой строки, а именно:

.

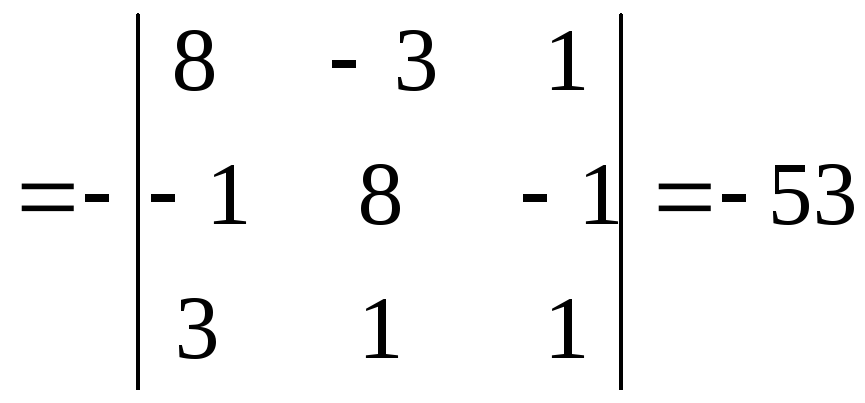Вычислим тот же самый определитель, образовывая нули в его третьем столбце и раскладывая полученный определитель по этому столбцу. Например, к элементам второй строки прибавим соответствующие элементы четвертой, предварительно умноженные на , а к элементам третьей – элементы той же четвертой строки (можно сказать – предварительно умноженные на 1). Получим

.

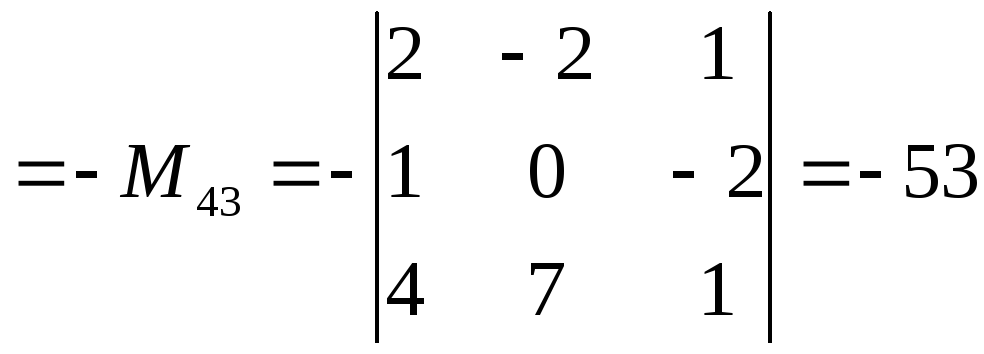Пример. Решить неравенство

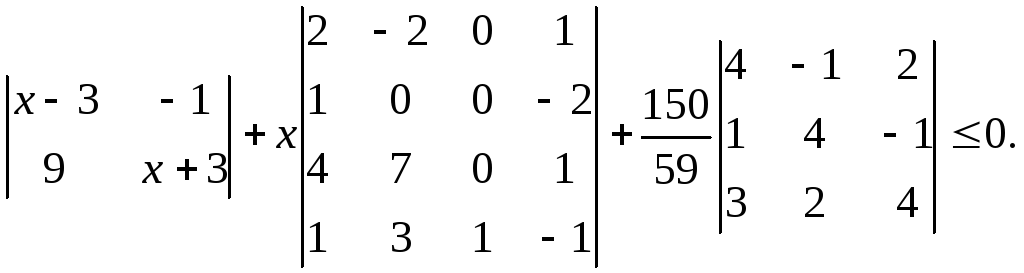
1-й шаг – вычисление определителей. Достаточно вычислить определители второго и третьего порядков, так как определитель четвертого порядка уже был вычислен в предыдущем примере (он равен –53). Имеем

на основании свойств определителей

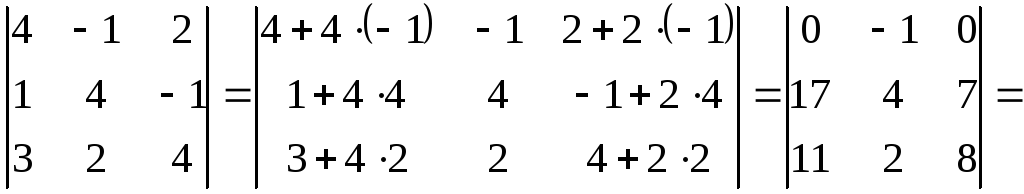
2-й шаг – решение неравенства .

Так как корни квадратного трехчлена равны 3 и 50, сразу получаем

.