- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
Пусть дана плоскость, заданная общим уравнением
![]() ,
( 27 )
,
( 27 )
и прямая, заданная своими параметрическими уравнениями
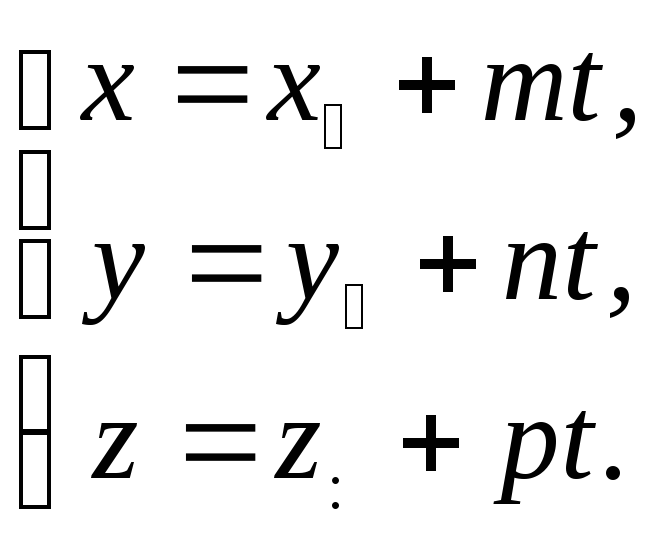 ( 28 )
( 28 )
Для отыскания возможной точки пересечения прямой и плоскости заменим в уравнении (27) значения x, y, z их значениями из уравнений (28), что даст нам уравнение относительно t,
![]() ,
,
![]() .
( 29 )
.
( 29 )
При рассмотрении последнего уравнения могут представиться три случая.
1)
![]() .
.
В этом случае мы решаем уравнение (29) относительно t,
![]() ;
;
далее замена t на
![]() в уравнениях (28) дает координаты искомой
точки пересечения.
в уравнениях (28) дает координаты искомой
точки пересечения.
2)
![]() ,
но
,
но
![]() .
.
В этом случае точка пересечения отсутствует, прямая параллельна плоскости, но не лежит в ней.
3)
![]() и
и
![]() .
.
В этом последнем случае точка лежит в плоскости, так как ее координаты удовлетворяют уравнению плоскости.
Таким же образом мы можем искать возможные
точки пересечения прямой с произвольной
поверхностью. Например, если поверхностью
является сфера радиуса R
с центром в точке
![]() ,
,
![]() ,
,
мы получаем следующее уравнение относительно t:
![]()
или
![]()
![]()
Последнее уравнение является квадратным относительно t и может иметь два, одно или ни одного решения. Соответственно мы получаем две, одну (случай касания прямой и сферы) или ни одной точки пересечения.
Пример. Найти точку пересечения прямой
![]()
и плоскости
![]() .
.
Сначала мы записываем параметрические уравнения прямой
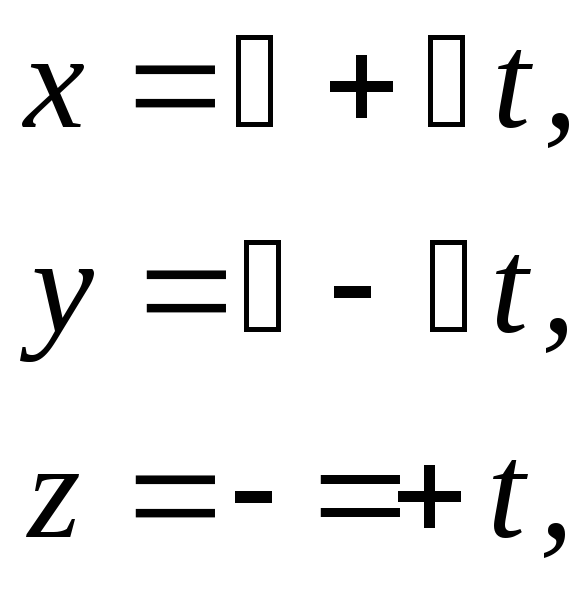
а затем действуем следующим образом:
![]()
![]() .
.
Ответ. Прямая пересекает плоскость в
точке
![]() .
.
Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
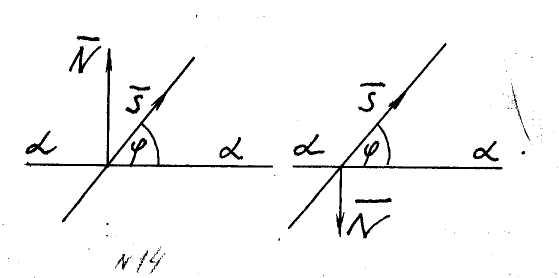
Как известно, углом между прямой l
и плоскостью![]() называется угол между этой прямой и ее
(ортогональ-ной) проекцией на плоскость.
называется угол между этой прямой и ее
(ортогональ-ной) проекцией на плоскость.
 Пусть
Пусть
![]() -- соответственно направляющий вектор
прямой l и нормальлный
вектор плоскости
-- соответственно направляющий вектор
прямой l и нормальлный
вектор плоскости
![]() соответственно (рис. 14). Как
Рис. 14 видно из
рисунка, угол
соответственно (рис. 14). Как
Рис. 14 видно из
рисунка, угол
![]() между l и
между l и![]() определяется одной из двух формул
определяется одной из двух формул
![]() или
или
![]() ,
,
откуда получаем
![]() ,
,
![]() .
( 30 )
.
( 30 )
Прямая и плоскость параллельны тогда
и только тогда, если их направляющий и
нормальный векторы
![]() перпендикулярны,
то есть
перпендикулярны,
то есть
![]() .
( 31 )
.
( 31 )
Прямая и плоскость перпендикулярны
тогда и только тогда, если их направляющий
и нормальный векторы
![]() коллинеарны,
то есть
коллинеарны,
то есть
![]() .
( 32 )
.
( 32 )
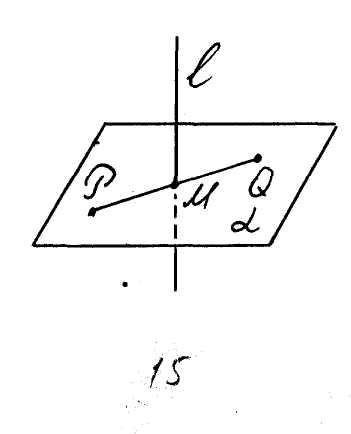 Пример. Найти точку, симметричную точке
Пример. Найти точку, симметричную точке
![]() относительно прямой (рис. 15)
относительно прямой (рис. 15)
![]() .
.
Найти проекцию точки P
на прямую и расстояние точки от
прямой.
Рис. 15
1) В качестве первого шага мы запишем
уравнение плоскости
![]() ,
проходящей через точку P
перпендикулярно данной прямой l.
В качестве нормального вектора плоскости
возьмем направляющий вектор прямой l
:
,
проходящей через точку P
перпендикулярно данной прямой l.
В качестве нормального вектора плоскости
возьмем направляющий вектор прямой l
:
![]() ,
откуда
,
откуда
![]()
![]() .
.
2) Теперь мы находим точку пересечения
M плоскости
![]() и прямой l,
и прямой l,
![]() ,
,
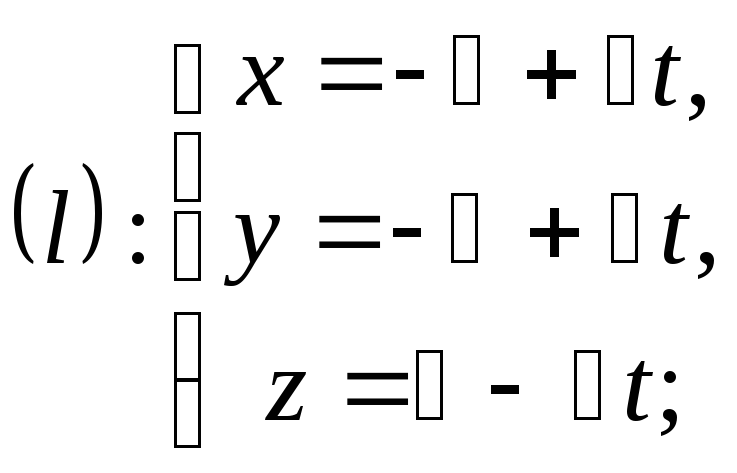
![]()
![]()
Найденная точка M является проекцией точки P на прямую l. Расстояние между точками M и P является расстоянием от точки P до прямой l (найдите его сами).
3) Наконец, мы находим искомую точку Q,
учитывая, что точка M
делит отрезок
![]() пополам. Получаем
пополам. Получаем
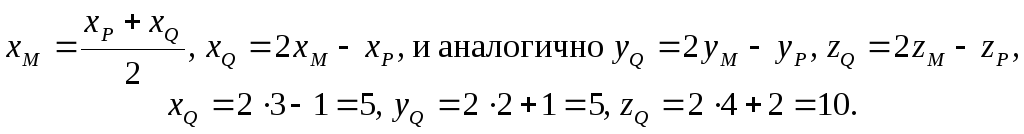
 Ответ. Искомая точка
Ответ. Искомая точка
![]() .
.
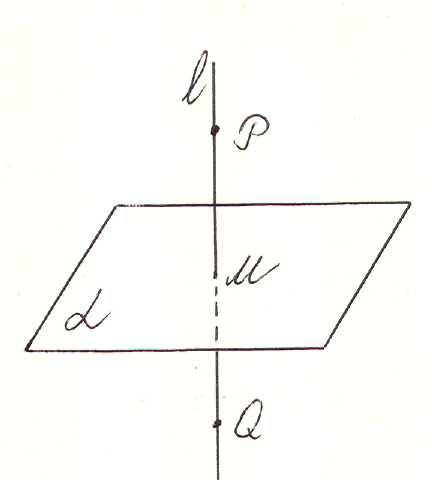
Пример. Найти точку Q,
которая симметрична точке
![]() относительно плоскости
относительно плоскости
![]() (рис. 16).
(рис. 16).
План решения задачи.
Рис.
16 1) Составляем параметрические
уравнения прямой l,
проходящей через точку P
перпендикулярно данной плоскости
![]() .
2) Находим точку пересечения M
прямой l и
плоскости
.
2) Находим точку пересечения M
прямой l и
плоскости
![]() .
.
3) Находим координаты искомой точки Q, принимая во внимание, что точка M является серединой отрезка PQ.
Осуществление плана.
1) В качестве направляющего вектора
![]() прямой
l возьмем нормальный
вектор
прямой
l возьмем нормальный
вектор
![]() плоскости
плоскости
![]() ,
откуда получаем параметрические
уравнения прямой
,
откуда получаем параметрические
уравнения прямой
![]() ,
проходящей через точку
,
проходящей через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() ,
,
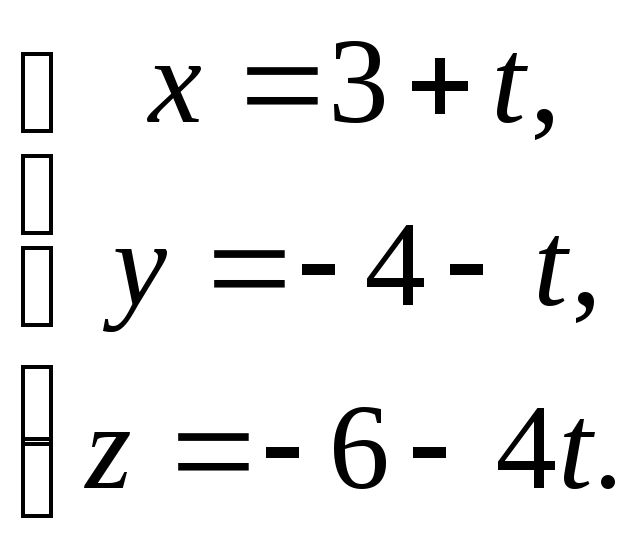
2) Подставляем правые части полученных уравнений в уравнение плоскости,
![]()
Найденное значение t подставляем в параметрические уравнения прямой, получая координаты точки М,
![]()
3) Наконец, находим координаты искомой точки Q,
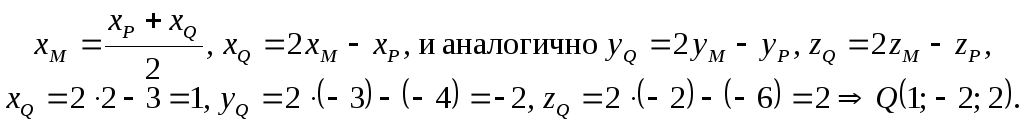
Пример. Составить уравнения высоты DE боковой грани ABD треугольной пирамиды с известными вершинами
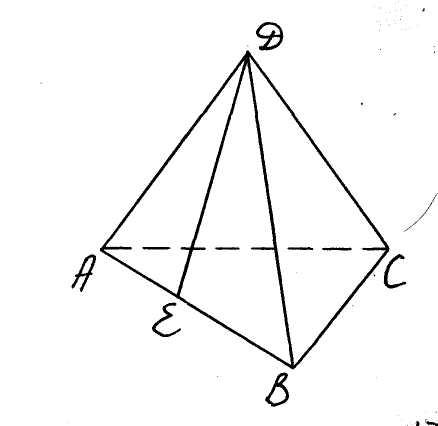
![]() (см. рис. 17).
(см. рис. 17).
План решения задачи.
1) Запишем параметрические уравнения прямой AB как прямой, проходящей через две точки, а именно, точ-ки A и B.
2) Составим уравнение плоскости
![]() ,
проходящей
Рис. 17 через
точку D перпендикулярно
прямой AB.
,
проходящей
Рис. 17 через
точку D перпендикулярно
прямой AB.
3) Найдем точку пересечения E
прямой AB и
плос-кости
![]() .
4) Составим уравнения искомой
высоты DE как
прямой, проходящей через две точки, а
именно, точки D и
E.
.
4) Составим уравнения искомой
высоты DE как
прямой, проходящей через две точки, а
именно, точки D и
E.
Осуществление плана.
1)
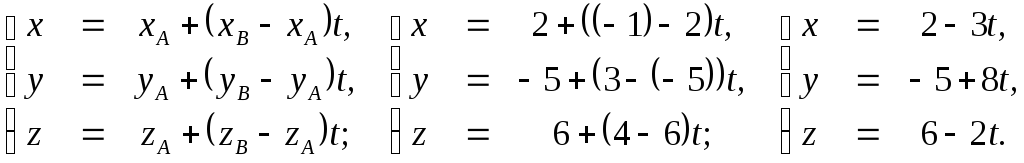
2) Чтобы составить уравнение плоскости
![]() ,
возьмем в качестве ее нормального
вектора направляющий вектор прямой АВ:
,
возьмем в качестве ее нормального
вектора направляющий вектор прямой АВ:
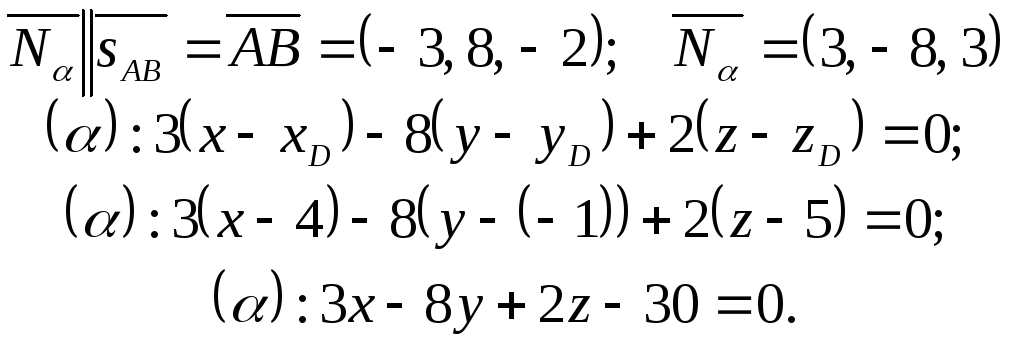
3) Находим точку пересечения прямой
![]() и
плоскости
и
плоскости
![]() :
:
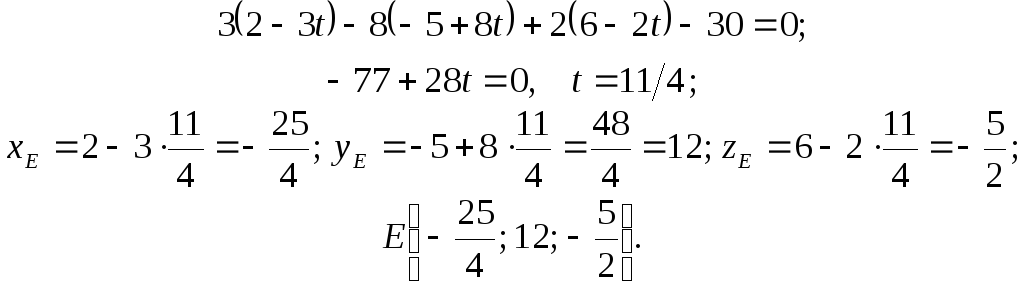
4) Составляем, наконец, параметрические и канонические уравнения искомой высоты боковой грани:
![]()