Ранг матрицы

Возьмем любые k строк и k столбцов матрицы A. Элементы матрицы, лежащие на пересечениях выделенных строк и столбцов, образуют определитель k-го порядка, который называется минором k-го порядка матрицы A.

Рангом матрицы, содержащей хотя бы один отличный от нуля элемент, называется наивысший порядок ее ненулевых миноров.

Будем обозначать ранг матрицы A символом .

Пример. Ранг матрицы

равен 2 ().

В самом деле, данная матрица содержит ненулевые миноры первого и второго порядков, например

.

Все 16 ее миноров третьего порядка, как можно проверить непосредственными вычислениями (затратив на это довольно много времени!), равны нулю, например

.

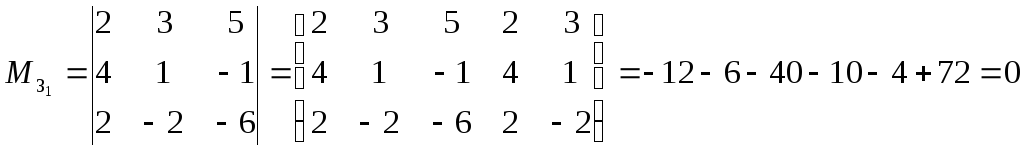
Единственный ее минор четвертого порядка, совпадающий с ее определителем (), также равен нулю, так как его можно разложить по любому его ряду (строке или столбцу) с коэффициентами – нулевыми минорами третьего порядка.

Итак, наивысший порядок ненулевых миноров данной матрицы равен 2, и на основании определения ранга матрицы получаем

.

Данный пример показывает, что нахождение ранга матрицы на основании определения представляет собой довольно трудоемкую процедуру. Не спасает положения и тот факт, что количество рассматриваемых миноров матрицы мо-жно уменьшить, ограничиваясь так называемыми окаймляющими минорами.

На практике чаще всего используются элементарные преобразования матрицы, не изменяющие ее ранг.

Элементарными называются следующие преобразования матрицы:

1) умножение любого ее ряда (то есть всех элементов любой ее строки или столбца) на произвольное число, отличное от нуля;

2) перемена местами любых двух ее рядов (строк или столбцов);

3) прибавление всех элементов какого-либо ряда, предварительно умноженных на любое число, к соответствующим элементам другого ряда;

4) отбрасывание любого ряда, состоящего только из нулей (короче – отбрасывание нулевого ряда).

Как уже сказано, элементарные преобразования не изменяют ранга матрицы, но позволяют свести его вычисление к вычислению ранга наиболее простой (в рассматриваемой ситуации) матрицы.

Пример. Найдем ранг матрицы предыдущего примера с помощью элементарных преобразований.

Переходя от одних матриц к более простым, мы будем обозначать неизменность ранга символом . Итак,

.

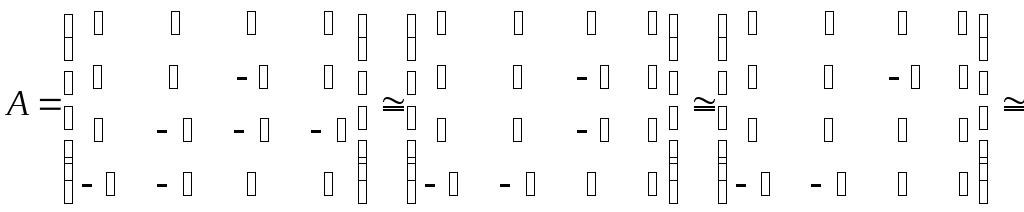
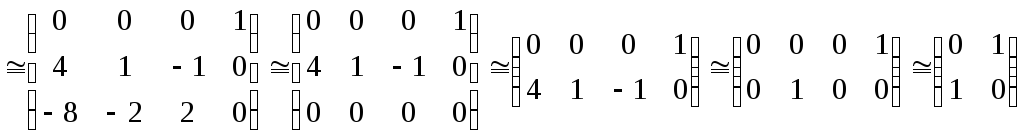В процессе работы были последовательно использованы следующие элементарные преобразования: а) прибавление первой строки к третьей; б) прибавление элементов второй строки, умноженных на -1, к соответствующим элемен-там третьей и деление на 4 элементов четвертого столбца; в) отбрасывание нулевой третьей строки; г) прибавление элементов второй строки, умноженных на 2, к соответствующим элементам третьей строки; д) отбрасывание нулевой тре-тьей строки; е) прибавление элементов второго столбца, умноженных на -4 и 1, соответственно к элементам первого и третьего столбцов; ж) отбрасывание нулевых первого и третьего столбцов.

Ранг последней (наипростейшей) матрицы равен 2,

,

так как она содержит два ненулевых минора первого порядка (достаточно и одного!), единственный ее минор второго порядка

отличен от нуля, а миноров высшего порядка, чем 2, матрица не содержит. Следовательно, ранг данной матрицы A также равен 2,

.

Найдите самостоятельно другие последовательности элементарных преобразований для отыскания ранга той же самой матрицы.