
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Уравнения некоторых линий в полярных координатах
1. Луч, исходящий из полюса под углом
![]() к полярной оси (рис. 13).
к полярной оси (рис. 13).
Для любой точки
![]() луча мы имеем
луча мы имеем
![]() .
( 19 )
.
( 19 )
2. Окружность радиуса R с центром в полюсе (рис. 14).
Для любой точки
![]() окружности имеем
окружности имеем
![]() .
( 20 )
.
( 20 )
3. Окружность
![]() (рис. 15).
(рис. 15).
|
|
0 |
|
|
|
|
|
1 |
|
|
0 |
|
|
2a |
a
|
a |
0 |
|
Point |
A |
|
|
O |
|
|
|
|
Запишем уравнение линии в декартовых
координатах. С этой целью умножим обе
его части на
![]() ,
,
![]() ,
,
и примем во внимание формулы (17), (18),
![]() .
.
Получили уравнение окружности радиуса
a с центром![]() .
.
4. Кардиоида
![]() .
С помощью таблицы мы изображаем сначала
несколько точек линии, а затем и саму
линию (см. рис. 16).
.
С помощью таблицы мы изображаем сначала
несколько точек линии, а затем и саму
линию (см. рис. 16).
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
||
|
|
1 |
½ |
0 |
-1/2 |
-1 |
|
||
|
+
|
2 |
3/2 |
1 |
½ |
0 |
|
||
|
|
2a |
3/2 a |
a |
1/2 a |
0 |
|
||
|
Точка |
A |
|
|
|
O |
|
||
|
|
|
|
||||||
5. Лемниската Бернулли9
![]() .
.
Линия симметрична относительно осей
Ox, Oy,
поэтому мы изучим ее в первом квадранте.
Очевидно, что
![]() .
Переходя к полярным координатам,
имеем
.
Переходя к полярным координатам,
имеем
![]()
![]() .
.
Давая значения 0,
![]() ,
,
![]() ,
,
![]() полярному углу
полярному углу
![]() ,
составим следующую таблицу и построим
лемнискату (рис. 17).
,
составим следующую таблицу и построим
лемнискату (рис. 17).
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
0 |
|
|
|
|
|
1 |
0.9 |
0.7 |
0 |
|
|
1 |
0.94 |
0.8 |
0 |
|
|
2a |
1.9 a |
1.6 a |
0 |
|
Точка |
A |
B |
C |
O |
6. Постройте самостоятельно спираль
Архимеда10
![]() (рис. 18).
(рис. 18).
7. Конические сечения в полярных координатах. Если мы поместим полюс в левом фокусе эллипса, правом фокусе гиперболы, в фокусе параболы соответственно и направим полярную ось от левого до правого фокусов эллипса и гиперболы и от вершины до фокуса параболы (см. рис. 19, 20, 21), то все три кривые будут иметь то же самое полярное уравнение.
■Пусть, во-первых,
![]() - произвольная точка эллипса. Тогда
- произвольная точка эллипса. Тогда
![]() ,
,
![]() ,
,
и на основании теоремы косинусов
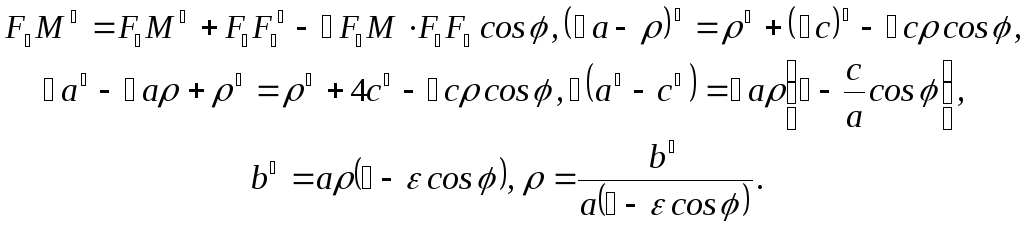
Введем следующую величину (так называемый параметр эллипса)
![]() .
.
Полярное уравнение эллипса принимает вид
![]() ,
,
где эксцентриситет
![]() удовлетворяет неравенству
удовлетворяет неравенству
![]() .
.
|
|
|
|
Для гиперболы мы тем же путем выводим
такое же самое уравнение, но в предположении,
что эксцентриситет
![]() (сделайте это самостоятельно).
(сделайте это самостоятельно).
Наконец, для параболы мы имеем (fig. 21)
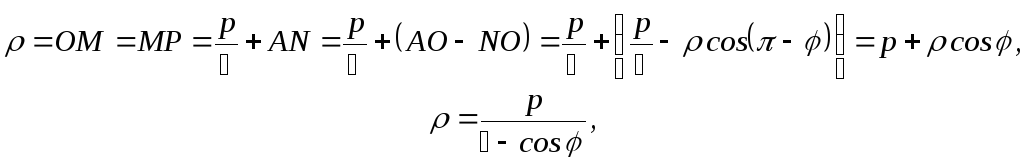
то есть то же самое уравнение с
эксцентриситетом
![]() .■
.■

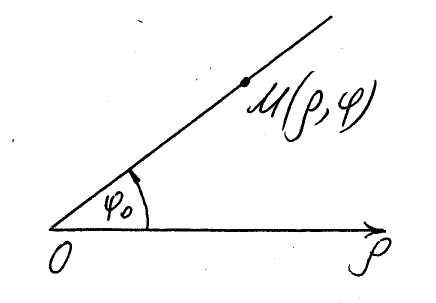 Рис. 13
Рис. 13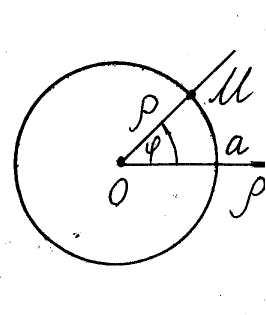 Рис . 14
Рис . 14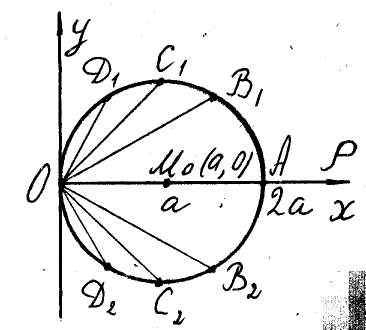 Рис . 15
Рис . 15
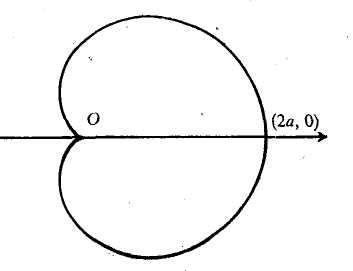 Рис. 16
Рис. 16
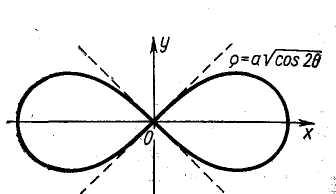 Рис.
17
Рис.
17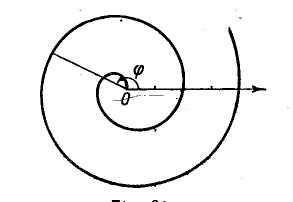 Рис. 18
Рис. 18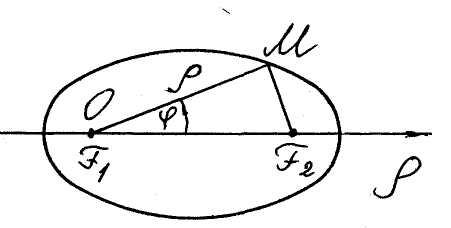 Рис. 19
Рис. 19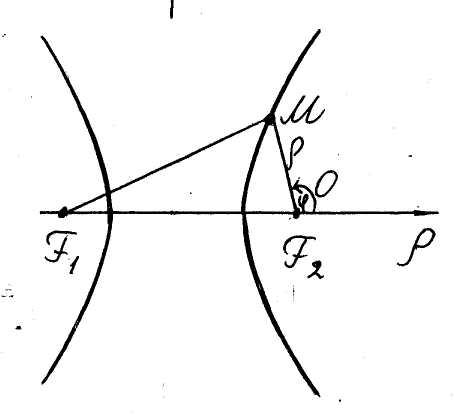 Рис. 20
Рис. 20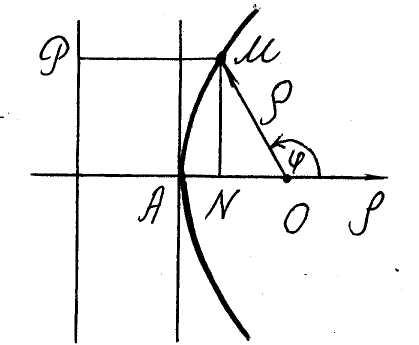 Рис. 21
Рис. 21