
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Уравнение плоскости, проходящей через три данные точки
|
|
|
|
Если
![]() - три данные точки плоскости (рис. 6), мы
можем составить ее уравнение с помощью
уравнения (4), определив нормальный
вектор из условия
- три данные точки плоскости (рис. 6), мы
можем составить ее уравнение с помощью
уравнения (4), определив нормальный
вектор из условия
![]() ( 12 )
( 12 )
и использовав одну из данных точек плоскости.
Пример. Составить уравнение плоскости,
которая проходит через три точки
![]() ,
,
![]() .
.
Последовательно имеем
![]()
![]() .
.
Использовав, например, точку
![]() ,
с помощью уравнения (4) получаем
,
с помощью уравнения (4) получаем
![]() ;
;
после раскрытия скобок записываем уравнение плоскости в общем виде
![]() .
.
Замечание. Если
студенты владеют теорией смешанного
произведения трех векторов, то уравнение
плоскости, проходящей через три данные
точки
![]()
![]()
![]() ,
можно получить из условия компланарности
трех векторов
,
можно получить из условия компланарности
трех векторов
![]() ,
,
где
![]() - произвольная
(текущая) точка плоскости. Именно:
- произвольная
(текущая) точка плоскости. Именно:
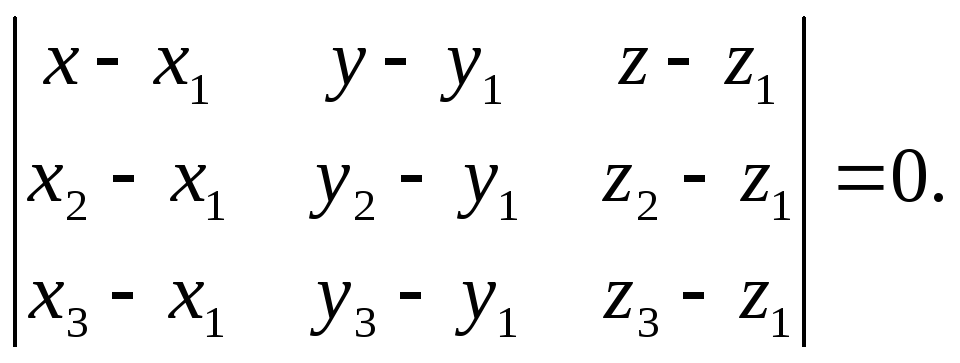
Уравнение плоскости в отрезках
Пусть плоскость
![]() отсекает отрезки
отсекает отрезки
![]() на координатных осях (см. рис. 7). Тогда
ее уравнение может быть представлено
в виде
на координатных осях (см. рис. 7). Тогда
ее уравнение может быть представлено
в виде
![]() .
( 13 )
.
( 13 )
Пример. Вычислить объем треугольной пирамиды, ограниченной плоскостью
![]()
и координатными плоскостями (рис. 7).
Перепишем сначала уравнение плоскости в форме (13),
![]() .
.
Плоскость отсекает на координатных
осях отрезки
![]() (так что
(так что
![]() ).
Следовательно, искомый объем равен
).
Следовательно, искомый объем равен
![]() кубических единиц..
кубических единиц..
Пример. Найти точки пересечения плоскости
![]() с координатными осями и линии ее
пересечения с координатными плоскостями.
изобразить плоскость.
с координатными осями и линии ее
пересечения с координатными плоскостями.
изобразить плоскость.
a) Точки пересечения с координатными осями
|
Точка пересечения с |
Полагаем |
Получаем |
|
осью Ox |
y = z = 0 |
|
|
осью Oy |
x = z = 0 |
|
|
осью Oz |
x = y = 0 |
|
b) Линии пересечения с координатными плоскостями
|
Линия пересечения с |
Полагаем |
Получаем |
|
плоскостью xOy |
z = 0 |
|
|
плоскостью xOz |
y = 0 |
|
|
плоскостью yOz |
z = 0 |
|
Плоскость изображена на рис. 8
Расстояние от точки до плоскости
Пусть даны плоскость
![]() ,
заданная общим уравнением
,
заданная общим уравнением
![]() ,
,
и точка
![]() .
Ее расстояние от плоскости дается
Рис. 9 формулой
.
Ее расстояние от плоскости дается
Рис. 9 формулой
![]() .
( 14 )
.
( 14 )
В соответствии с формулой мы должны в
уравнении плоскости заменить x,
y, z
координатами точки, найти абсо-лютную
величину результата и разделить его на
длину нор-мального вектора плоскости.
Пример. Найти уравнение сферы, центр
которой находится в точке
![]() и которая касается пло-скости
и которая касается пло-скости![]() .
.
Радиус сферы равен расстоянию от точки до плоскости. По формуле (14) имеем
![]() ,
,
 и
на основании (2) получаем уравнение
искомой сферы
и
на основании (2) получаем уравнение
искомой сферы
![]() .
.
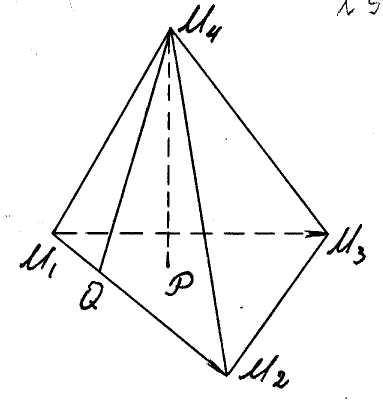
Пример. Найти объем треугольной пирамиды
с известными вершинами
![]() ,
,
![]() (рис. 10).
(рис. 10).
Если
![]() - высота пирамиды, то ее объем
Рис. 10 равен
- высота пирамиды, то ее объем
Рис. 10 равен
![]() .
.
Но
![]()
где
![]()
![]() ,
,
а высота
![]() равна расстоянию точки
равна расстоянию точки
![]() от плоскости, проходящей через точки
от плоскости, проходящей через точки
![]() .
Уравнение последней найдено выше,
.
Уравнение последней найдено выше,
![]() ,
,
откуда
![]() .
.
Окончательно
![]() кубических единиц.
кубических единиц.

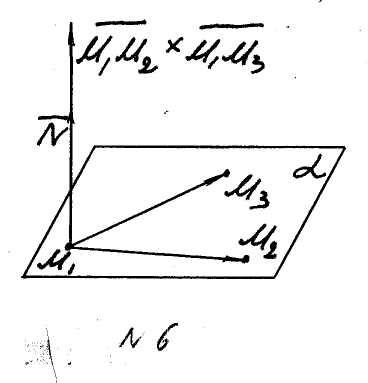 Рис. 6
Рис. 6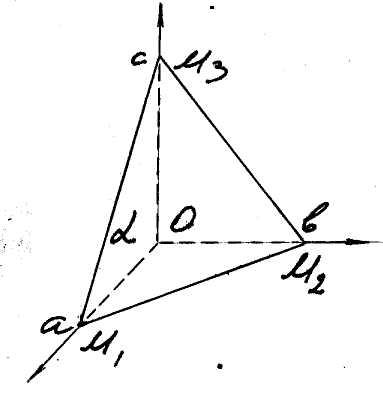 Рис. 7
Рис. 7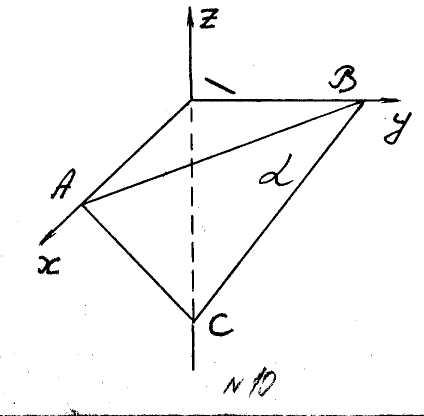 Рис. 8
Рис. 8