
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
-
Сформулировать определение линии.
-
Что такое текущие координаты?
-
Как найти точки пересечения двух линий?
-
Записать уравнение окружности данного радиуса с центром: а) в начале координат; б) в произвольной точке.
-
Как, имея уравнение окружности, написать уравнения ее левой, правой, нижней и верхней полуокружностей?
-
Что такое угловой коэффициент прямой?
-
Перечислить и записать основные уравнения прямой (на плоскости).
-
Как найти угловой коэффициент прямой, заданной: а) двумя известными ее точками; б) ее общим уравнением.
-
Сформулировать необходимое и достаточное условие параллельности двух прямых.
-
Сформулировать необходимое и достаточное условие перпендикуляр-ности двух прямых.
-
Сформулировать определение эллипса, написать его каноническое урав-нение, указать координаты фокусов и вершин, написать формулу для на-хождения эксцентриситета. Изобразить эллипс.
-
Тот же вопрос для гиперболы
-
Дать определение параболы, написать ее каноническое уравнение
Векторы
Приступая к изучению темы, студент должен четко усвоить ее первичные понятия: вектор (или геометрический вектор), модуль (или длина) вектора, нулевой и единичный векторы, орт данного вектора11, равные и противоположные векторы, коллинеарные12 (в том числе сонаправленные и противоположно направленные) и компланарные13 векторы, угол между векторами, линейные операции над векторами и их свойства, проекция вектора на ось, свойства проекций.
Проекция вектора на ось
|
|
|
|
Пусть дана некоторая ось u,
направление которой определяется ортом
(единичным вектором того же направления)
![]() ,
и вектор
,
и вектор
![]() (см. рис. 1).
(см. рис. 1).
Вектор
![]() ,
образованный проекциями
,
образованный проекциями
![]() точек
точек
![]() на ось, называется, как известно,
составляющей вектора
на ось, называется, как известно,
составляющей вектора
![]() вдоль оси. Составляющая может быть
направлена вдоль оси, а может иметь
противоположное направление.
вдоль оси. Составляющая может быть
направлена вдоль оси, а может иметь
противоположное направление.
Проекцией вектора на ось (![]() )
в первом случае называется длина его
составляющей вдоль оси, а во втором
случае – та же длина, взятая с
противоположным знаком.
)
в первом случае называется длина его
составляющей вдоль оси, а во втором
случае – та же длина, взятая с
противоположным знаком.
Пример. Для векторов
![]() ,
представленных на 2,
,
представленных на 2,
![]() ,
,
так как составляющая
![]() вектора
вектора
![]() имеет длину 4 и направлена вдоль оси, а
составляющая
имеет длину 4 и направлена вдоль оси, а
составляющая
![]() вектора
вектора
![]() имеет длину 3 и направлена противоположно
оси.
имеет длину 3 и направлена противоположно
оси.
Если
![]() - угол между вектором
- угол между вектором
![]() и осью u (то есть
угол между ортами вектора и оси), то
проекция вектора на ось может быть
найдена по формуле
и осью u (то есть
угол между ортами вектора и оси), то
проекция вектора на ось может быть
найдена по формуле
![]() ( 1 )
( 1 )
(проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью).
Пример. Вектор
![]() длины 16 образует угол
длины 16 образует угол
![]() с осью u. Его
проекция на ось на основании формулы
(1) равна
с осью u. Его
проекция на ось на основании формулы
(1) равна
![]() .
.
Необходимо знать основные свойства проекций: 1) проекция суммы векторов равна сумме их проекций; 2) числовой (и вообще скалярный) множитель можно вынести за знак проекции.
Разложение вектора по базису
Как известно, базисом на плоскости (в пространстве) называется упорядоченная пара неколлинеарных векторов (соотв. упорядоченная тройка некомпланарных векторов), приведенных к общему началу.
Теорема 1. Любой вектор на плоскости (соотв. в пространстве) может быть единственным способом разложен по базису.
Пусть, например,
![]() ( 2 )
( 2 )
- базис в пространстве. Теорема означает,
что для любого пространственного вектора
![]() существует единственная тройка чисел
существует единственная тройка чисел
![]() (координат вектора в данном базисе)
такая, что имеет место следующее
разложение
(координат вектора в данном базисе)
такая, что имеет место следующее
разложение
![]() .
( 3 )
.
( 3 )
Из теоремы 1 вытекает, что два вектора равны тогда и только тогда, если они имеют одинаковые координаты.
Два вектора коллинеарны тогда и только тогда, если их соответствующие координаты пропорциональны.
Пример. Найти значения параметров m
и n, при которых
два данных вектора
![]() коллинеарны.
коллинеарны.
Из условия пропорциональности соответствующих координат коллинеарных векторов имеем
![]() .
.
Ответ: векторы коллинеарны при
![]() .
.
Теорема 2. Линейным операциям над векторами соответствуют такие же операции над их координатами.
Например, произведением вектора
![]() на число (скаляр)
на число (скаляр)
![]() является вектор
является вектор
![]() ,
,
то есть вектор с координатами
![]() .
Суммой векторов
.
Суммой векторов
![]()
является вектор
![]()
с координатами
![]() .
.
На основании теоремы 2 мы можем отождествлять любой вектор со строкой его координат в данном базисе и писать, например,
![]() .
.
Вместо фигурных скобок часто используются круглые. Координаты векторов можно разделять и запятыми, если это не приводит к недоразумениям.
Пример. Найти вектор
![]() ,
если известны векторы
,
если известны векторы
![]() .
.
На основании теоремы 2 имеем
![]()
![]() .
.
Базис (2) определяет систему координат
в пространстве. Началом координат
является общее начало О базисных
векторов, координатные оси
![]()
![]()
![]() направлены вдоль векторов
направлены вдоль векторов
![]() ,
единица масштаба на каждой оси равна
модулю (длине)
,
единица масштаба на каждой оси равна
модулю (длине)
![]() соответствующего базисного вектора.
соответствующего базисного вектора.
Для любой точки
![]() пространства вектор
пространства вектор
![]() называется радиус-вектором этой
точки, причем координаты радиус-вектора
совпадают с координатами этой точки,
называется радиус-вектором этой
точки, причем координаты радиус-вектора
совпадают с координатами этой точки,
![]() ,
или просто
,
или просто
![]() .
( 4 )
.
( 4 )
Пример. Найти вектор, зная координаты его начала А и конца В.
Пусть, например,
![]() .
Тогда вектор
.
Тогда вектор
![]() равен разности радиус-векторов точек
А, В,
равен разности радиус-векторов точек
А, В,
![]() ,
,
и по теореме 2
![]() ( 5 )
( 5 )
Таким образом, координатами вектора
![]() являются разности соответствующих
координат его конца и начала.
являются разности соответствующих
координат его конца и начала.
Например,
![]() .
.
Пример. Разложить вектор![]() по
векторам
по
векторам
![]()
![]()
![]() .
Могут ли векторы
.
Могут ли векторы
![]() образовывать базис в пространстве?
образовывать базис в пространстве?
Мы должны найти такие три числа
![]() ,
чтобы выполнялось равенство
,
чтобы выполнялось равенство
![]() .
.
Но
![]()
Приравнивая соответствующие координаты
векторов
![]() и
и
![]() ,
получаем систему линейных алгебраических
уравнений относительно
,
получаем систему линейных алгебраических
уравнений относительно
![]()
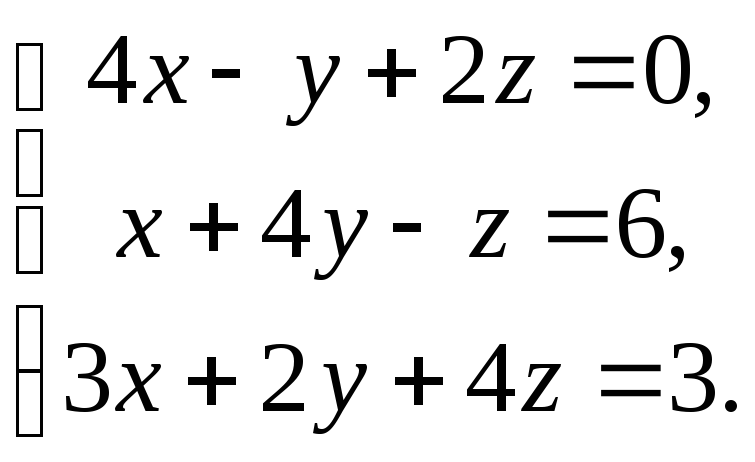
Главный определитель системы отличен от нуля,
![]() ,
,
следовательно, она имеет единственное решение. Вспомогательные определители системы равны
![]() ,
,
откуда на основании правила Крамера
![]() ,
,
и искомое разложение вектора
![]() есть
есть
![]() .
.
Анализ решения показывает, что по
векторам
![]() может быть разложен любой другой
пространственный вектор, так как решение
соответствующей задачи приводит к
системе уравнений с той же левой частью
и тем же самым главным определителем,
что и в только что решенном примере, и
с правыми частями - координатами
названного вектора. Следовательно,
векторы
может быть разложен любой другой
пространственный вектор, так как решение
соответствующей задачи приводит к
системе уравнений с той же левой частью
и тем же самым главным определителем,
что и в только что решенном примере, и
с правыми частями - координатами
названного вектора. Следовательно,
векторы
![]() могут образовывать базис в пространстве,
и только что найденные числа
могут образовывать базис в пространстве,
и только что найденные числа
![]() являются координатами вектора
являются координатами вектора
![]() в этом базисе.
в этом базисе.
В общем случае мы можем сказать, что три пространственных вектора
![]() ( 6 )
( 6 )
могут образовывать базис в пространстве тогда и только тогда, если определитель третьего порядка, образованный координатами векторов, отличен он нуля,
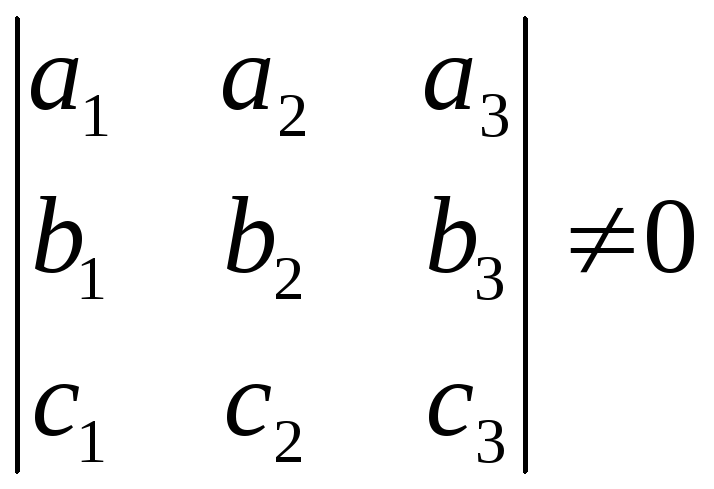 .
( 7 )
.
( 7 )
Равенство (7) является также необходимым и достаточным условием некомпланарности трех пространственных векторов (6).
Пример. Могут ли образовывать базис в пространстве три данных вектора
![]() ?
?
Решение. Определитель, составленный из координат векторов,
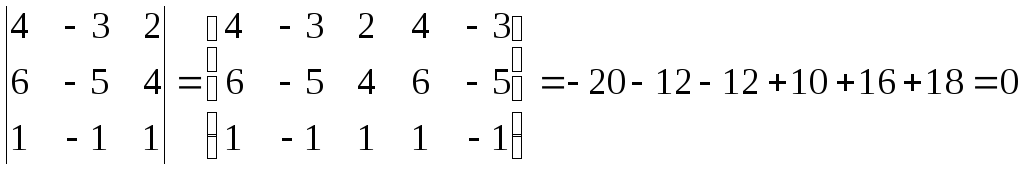 ,
,
равен нулю. Следовательно, векторы не являются некомпланарными и не могут образовывать базис в пространстве.

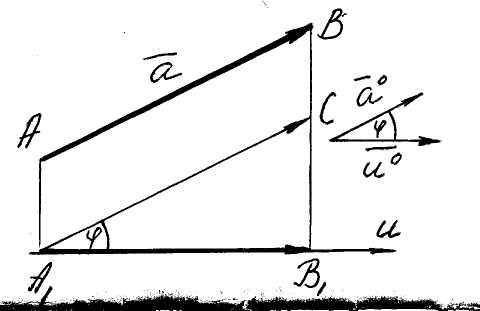 Рис. 1
Рис. 1
 Рис. 2
Рис. 2