1.5. Марковские процессы

1.5.1. Понятие о стохастических процессах

Стохастический процесс представляет собой множество случайных величин, образующих упорядоченную последовательность.

Последовательность случайных величин в процессе можно представить в виде X(t), где t – параметр процесса (обычно время).

Значения, принимаемые случайными величинами в процессе, образуют пространство состояний.

На рис. 1.15 показана конкретная реализация процесса на отрезке времени (t₀, t_n–1). По оси абсцисс отложен дискретный параметр процесса t, а по оси ординат – дискретная случайная величина X, которая является множеством и включает в себя семь состояний объекта наблюдения (S₀–S₆). В данном случае множество X является пространством состояний (X{S₀, S₁, S₂, S₃, S₄, S₅, S₆}). Для параметра процесса t_i X(t_i) = S₂.

В большинстве прикладных задач целью является вычисление безусловного распределения случайной величины X(t_n), которое зависит только от реализации процесса в интервале от t_n–1 до t_n.

Рис. 1.15. Конкретная реализация процесса в интервале (t0, tn–1)

1.5.2. Марковские процессы

Существует важный класс стохастических процессов, в которых вероятность случайной величины в момент времени t_n зависит от значения случайной величины в момент времени t_n–1 и не зависит от конкретного вида реализации процесса до времени t_n–1. Такой процесс называют процессом без последствия. Процессы, обладающие этим свойством, называют Марковскими процессами.

В Марковском процессе параметр t и пространство состояний X(t) могут быть как дискретными, так и непрерывными. Мы рассмотрим только процессы с непрерывными параметрами, при этом будем иметь в виду только дискретные и конечные пространства состояний.

Рассмотрим Марковский процесс X(t) с непрерывным временным параметром t. Введём обозначения: t_n–1 = t, t_n = t + t.

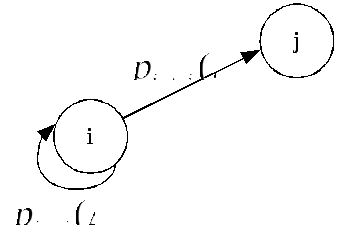
В процессе рассмотрим два состояния: i-е, в котором находится объект в момент времени t_n–1; j-е, в которое объект может перейти, а может и не перейти в момент времени t_n (рис. 1.16). Тогда вероятность перехода из i-го состояния в j-е запишется следующим образом:

.

(1.57)

Рис. 1.16. Переход из состояния i в состояние j или в само себя

Будем рассматривать только однородные Марковские процессы, в которых p_ij зависят только от t.

Тогда при t→0 вероятности переходов принимают вид

,

(1.58)

.

(1.59)

Здесь p_i→i(t) – вероятность того, что за промежуток времени t не произойдёт смены состояния процесса при условии, что процесс находится в состоянии i в начале этого промежутка.

q_i→j, q_j→i – интенсивности переходов из состояния i в состояние j и наоборот;

q_i – интенсивность перехода из состояния i в любое другое состояние, кроме состояния i:

,

(1.60)

где n – число всех возможных состояний.

Так как события «переход из i-го в j-е состояние» (ij) и «переход из i-го в i-е состояние» (ii) являются полной группой событий, то

.

(1.61)

Во многих приложениях требуется определить безусловные вероятности состояний для момента времени (t + t), зная вероятности состояний в момент времени t (рис. 1.17).

Для этого используется метод пространства состояний, в котором используется система дифференциальных уравнений Чемпена – Колмогорова (см. п 5.1).

Рис.1.17. Возможные переходы для процесса, в котором объект может находиться в трех состояниях