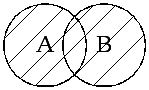Глава 1. Основные положения теории вероятности

1.1. Множества

1.1.1. Определение понятия «множество»

Множество представляет собой некоторый набор определённых элементов, в общем случае неупорядоченных и не образующих последовательности. Множества могут иметь бесконечное и конечное число элементов или не иметь элементов вообще (бесконечное множество – натуральные числа; конечное множество – колода карт).

Множество записывается в следующем виде: А = {X₁, X₂, …, X_к, …, X_n}, где Х_к – элемент множества А.

1.1.2. Соотношения между двумя множествами

Они зависят от того, имеют ли эти множества общие элементы.

Для двух множеств А и В существуют следующие возможности:

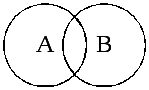
1) А и В имеют общие элементы, но каждое из множеств имеет также элементы, не принадлежащие другому множеству. Говорят, что множества пересекаются: А  В = С (рис. 1.1).

Рис. 1.1. Диаграмма Вьенна при пересечении двух множеств

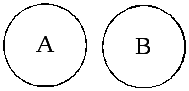
2) А и В не имеют общих элементов (взаимоисключающие множества или непересекающиеся) (рис. 1.2).

Рис.1.2. Диаграмма Вьенна для непересекающихся множеств

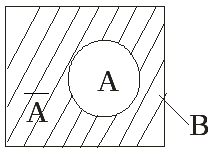
3) А целиком включает В (рис. 1.3).

Рис. 1.3. Диаграмма Вьенна для случая, когда множество А целиком включает В

В этом случае В является подмножеством А.

1.1.3. Операции с множествами

1) Объединение двух множеств – это множество С, которое содержит все элементы, принадлежащих ему множеств (рис. 1.4).

Рис. 1.4. Диаграмма Вьенна при объединении двух множеств

Математическая запись операции: А  В = С.

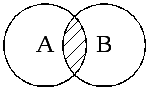
2) Пересечение двух множеств (А  В = С) – это множество С, которое содержит элементы, являющиеся общими для обоих множеств (рис. 1.5).

Рис.1.5. Диаграмма Вьенна при пересечении двух множеств

3) Разность двух множеств (А – В = С) – это множество С, состоящее из тех элементов А, которые не являются элементами множества В (рис. 1.6).

Рис. 1.6. Диаграмма Вьенна при разности двух множеств

Следует отметить, что А – В  В – А.

4) Дополнение множества А. Определим множество В как множество всех элементов, рассмотренных в данной ситуации (рис. 1.7). Дополнением множества А называется множество A, состоящее из элементов, которые не входят в множество А.

Рис.1.7. Диаграмма Вьенна при разности двух множеств

При этом A  A = 0 и A  A = B.

1.2. События

Событие в теории вероятности связывается с исходами многократно повторяющихся экспериментов. Каждое действие или испытание в ходе эксперимента приводит к некоторому исходу, который может оказаться неодинаковым для различных испытаний.

Множество всех возможных исходов называется пространством элементарных событий и обозначается .

Для кубика  = {1, 2, 3, 4, 5, 6}.

Событием называется подмножество (пространств элементарных событий), которое включает в себя все исходы, удовлетворяющие некоторому критерию, где в каждом испытании событие происходит либо не происходит в зависимости от того, где находится исход данного испытания.

Подобно тому, как это делалось для множеств, можно определить операции для событий:

1) Объединение двух событий Е_А и Е_В – это событие, заключающееся в том, что происходит либо событие Е_А, либо событие Е_В, либо оба события вместе (Е_А  Е_В).

Пример. Рассмотрим два множества, которые получаются при бросании двух костей: Е₁ = {2,6;6,2;4,4;3,5;5,3} – событие, для которого сумма выпавших очков равна 8, и Е₂ = {1,1; 2,2; 3,3;…6,6} – событие, в котором на каждой кости выпало одинаковое число очков. Тогда

Е₃ = Е₁  Е₂ = {1,1; 2,2; 3,3…;6,6}.

Получим событие, которое включает все элементы событий Е₁ и Е₂.

2) Пересечение двух событий Е_А и Е_В – это событие, заключающееся в том, что происходят оба события вместе Е_А и Е_В (Е_А  Е_В).

Е₁  Е₂ = {4,4}.

3) Дополнение события Е_А – это событие E_А, заключающееся в том, что само событие Е_А не произошло.

Объединение события и его дополнения даст пространство элементарных событий. Это событие называется достоверным событием.

Е_А  Е_В = .

Событие и его дополнение являются противоположными событиями. Дополнение достоверного события называется невозможным событием и обозначается . При этом  = Ω, где  – это пустое множество, не содержащее никакого исхода эксперимента.

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

События называются независимыми, если вероятность наступления одного из них не зависит от вероятности наступления или не наступления другого; в противном случае события называются зависимыми (см. раздел «Условная вероятность»).

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.