Exercices

69) Traduire symboliquement par une égalité chacune des phrases suivantes.

a) L’image de 5 par la fonction f est égale à 4.

b) 5 est l’image de -3 par la fonction f.

c) 2 a pour image 0 par la fonction f.

d) Les images de 2 et de 4 par la fonction f sont nulles.

e) Les nombres qui ont pour image 5 par la fonction f sont -3 et 0.

f) 1 est l’image des nombres -2 et 1 par la fonction f.

70) Traduire chaque égalité par une phrase, en utilisant le mot «image ».

a) f (-2) = 1 b) f (x) = -2 c) g (4) = 0 d) b = g (0) e) y = f (x) f) v = f (t)

71) La courbe suivante représente une fonction f définie sur [-6 ; 8]. Elle passe par les points A (-3 ; 2) ; B (0 ; 3) ; C (2 ; 5) et M (x ; y). Traduire par une égalité chacune des phrases suivantes.

a) L’abscisse du point A a pour image 2 par la fonction f.

b) L’image de 0 par la fonction f est l’ordonnée du point B.

c) La fonction f associe, à l’abscisse du point C, l’ordonnée du point C.

d) L’ordonnée du point M est l’image par la fonction f de l’abscisse du point M.

72) Traduire chaque proposition par une seule égalité.

a) 3 est l’image de 5 par la fonction f.

b) -2 a pour image 0 par la fonction f.

c) f est la fonction qui, à tout nombre réel x, associe son opposé.

d) Pour x = 4, on a f (x) = 1.

e) f est la fonction qui, à toute longueur x (en cm) de l’arête d’un cube, associe l’aire totale (en cm²) du cube.

73) Soit f la fonction définie sur D = [-3 ; 3] dont la représentation graphique est la courbe suivante passant par les points A, B, C.

Recopier et compléter les phrases suivantes.

a) Le point A (… ; …) appartient à la courbe représentative de f.

b) -3 appartient à D et a pour image … par la fonction f.

c) La courbe représentative de f passe par le point B (… ; …).

d)… D et f (…) = … .

74) Traduire chacune des propositions suivantes par une ou des égalités d’images.

a) La courbe représentative de la fonction f passe par le point A (-3 ; 5).

b) Le point B d’abscisse -2 de la courbe représentative de la fonction f a pour ordonnée 3.

c) La courbe représentative de la fonction f coupe l’axe des ordonnées au point d’ordonnée -2.

d) La courbe représentative de la fonction f coupe l’axe des abscisses en

-1 et 4.

e) La fonction g est représentée graphiquement par une courbe qui passe par le point M d’abscisse -3 et d’ordonnée 1.

f) La courbe représentative de la fonction g passe par l’origine du repère.

75) La courbe suivante représente une fonction f dans un repère.

a) Sur quel intervalle la fonction f est-elle définie ?

b) Déterminer graphiquement l’image par f de : -3 ; -2 ;-1 ; 0 ; 1 ; 2 ; 3 ; 4 ; 5.

c) Quels sont les nombres x qui ont pour image 1 par la fonction f ?

d) Quels sont les nombres x qui ont pour image 0 par la fonction f ?

e) Déterminer deux nombres x qui ont la même image par la fonction f.

76) La courbe suivante est la représentation graphique d’une fonction f dans un repère.

a) Quel est l’ensemble de définition de la fonction f ?

b) Déterminer graphiquement : f (-1) ; f(0) ; f(1) ; f(2) ; f(3) ; f(4) ; f(6).

c) Déterminer, avec la précision permise par le graphique, une valeur approchée de f () et de f(5).

d) Quels sont les nombres x tels que f(x) = 2 ?

e) Quels sont les nombres x tels que f(x) = 0 ?

77) Soit g la fonction définie, pour tout nombre réel x différent de 2, par .

a) Déterminer g(0) ; g (-2) ; g () ; g(-).

b) Quel est l’ensemble de définition de g ?

c) Existe-t-il des nombres réels x tels que g(x) = 0 ?

78) Soit h la fonction définie, pour tout nombre réel x non nul, par .

a) Quel est l’ensemble de définition de h ?

b) Calculer l’image par h des nombres suivants : 1 ; -1 ;  ;  ;  ;

c) Déterminer le signe des nombres h (500) et h (-500).

d) Quels sont les réels x qui ont une image strictement négative par la fonction h ?

e) Existe-t-il des réels x qui ont une image nulle par h ?

f) Existe-t-il des réels x tels que :

79) Déterminer, dans chaque cas, l’ensemble de définition des fonctions.

a) b) c)

d) e) f)

x	- 4			4
f(x)		- 4	4

80) Soit f est la fonction définie sur R par . Recopier et compléter le tableau de valeurs suivant :

81) Soit f la fonction définie sur R par Dresser un tableau de valeurs de f sur l’intervalle [-3 ; 3] avec un pas de 0,5.

Recopier et compléter les phrases suivantes :

a) 1,5 a pour image … par la fonction f.

b) … a pour image 1,5 par la fonction f. (On admettra que la valeur 1,5 n’est atteinte qu’une seule fois.)

c) 1,5 est l’image de … par la fonction f.

d) f(1,5) est l’image de … par la fonction f.

82) Soit f la fonction définie sur R par Dresser un tableau de valeurs de f sur l’intervalle [-6 ; 6] avec un pas de 1.

Recopier et compléter les phrases suivantes :

a) … est l’image de -3 par la fonction f.

b) … a pour image -3 par la fonction f. (On admet que la valeur -3 n’atteinte qu’une seule fois.)

c) -3 a pour image … par la fonction f.

d) f (-3) est l’image de … par la fonction f.

83) Dans chaque cas, déterminer l’ensemble de définition de la fonction f.

a) b) c) d)

84) Dans chaque cas, déterminer l’ensemble de définition de la fonction f.

a) b)c) d)

85) Dans chaque cas, déterminer l’ensemble de définition de la fonction f.

a) b)c) d)

86) Soit la fonction f définie par Les points A(2 ; 8) ; B(-3 ; 4) ; et C( ; 1) appartiennent-ils à la représentation graphique de f ?

87) Soit la fonction f définie sur R parDéterminer l’ordonnée du point de la représentation graphique dont l’abscisse est égale à -2. Déterminer les abscisses des points de la représentation graphique dont l’ordonnée est égale à 1.

88) Soit la fonction f définie sur R par Quelle valeur doit-on donner à m pour que la courbe représentative f passe par le point de coordonnées

(-2 ; 4) ?

89) Soit la fonction f définie sur R par Calculer les images respectives des nombres 0 ; -1 et 3 par la fonction f. Quelle remarque est-il possible de faire ?

90) Soit f est une fonction définie pour tout réel x sauf par

a) Déterminer les images par f de 4 ; -2 ; 7 ; 0,5 et 5.

b) Déterminer les antécédents par f de 2.

c)Soit la courbe représentative de f dans un repère. Déterminer, s’ils existent, les coordonnées des points d’intersection de la courbe représentative avec l’axe des abscisses.

91) La courbe, représentant une fonction f, passe par le point A (-2 ; 3). La fonction f est définie sur R par

a) Déterminer le réel a.

b) Calculer f () en le mettant sous la forme n + n₁où n et n₁ sont des entiers naturels.

92) Soit une fonction f définie sur R. Traduire chacun des renseignements suivants par une écriture faisant intervenir f.

a) La courbe représentative passe par l’origine du repère.

b) Le point d’abscisse -1 de la courbe représentative a pour l’ordonnée -4.

c) Le point d’ordonnée 4 de la courbe représentative a pour l’abscisse 5.

d) La courbe représentative coupe l’axe des abscisses aux points d’abscisses -3 et 2.

93) La courbe suivante est la représentation graphique d’une fonction f.

a) Quel est l’ensemble de définition de la fonction f ?

b) Déterminer graphiquement f (1) ;

f (2) ; f (3) ; f (4) ; f(0) ; f (-1).

c)Résoudre graphiquement les équations suivantes : f (x)=1 ; f (x)=3 ; f (x)=0 ; f (x)= 2 ; f (x)=4 ; f (x)= -1.

94) La courbe suivante est la représentation graphique d’une fonction f définie sur [-5 ; 5].

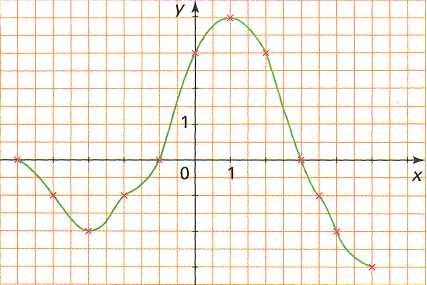
a) Résoudre graphiquement les équations suivantes : f (x)=3 ; f (x)=0 ; f (x)= -2 ; f (x)= -1.

b) Résoudre graphiquement les inéquations suivantes : f (x) > 3 ;

f (x)> -2 ; f (x) < - 1 ; f (x) 0.

95) La courbe suivante représente une fonction f.

a)Quel est l’ensemble de définition de la fonction f ?

b) Résoudre graphiquement les équations et inéquations suivantes :

f (x)= 2 ; f(x) > 2; f(x) 2; f (x)= -1 ; f(x) 1 ; f(x) < - 1.

96) La courbe suivante représente une fonction f.

a) Sur quel intervalle la fonction f

est-elle définie ?

b) Déterminer graphiquement l’image par f de -2 et celle de -1.

c) Déterminer graphiquement : f(0) ; f(3) ; f(5).

d) Résoudre graphiquement les équations suivantes : f(x)= -2 ; f(x)=1 ; f (x) = 3 ; f (x) = -3.

e) Résoudre graphiquement les inéquations suivantes : f (x) 1 ;

f (x)< -2 ; f (x) > - 3 ; f (x) 3.