Exercices
207) x
désignant un réel quelconque, exprimer :
en fonction de cos x et de sin x.
208)
Exprimer
et
en
fonction de tan x. Donner la valeur exacte de
209) Démontrer que pour tout x réel
a)
b)
c)
d)
210)
Simplifier
l’écriture des nombres suivants :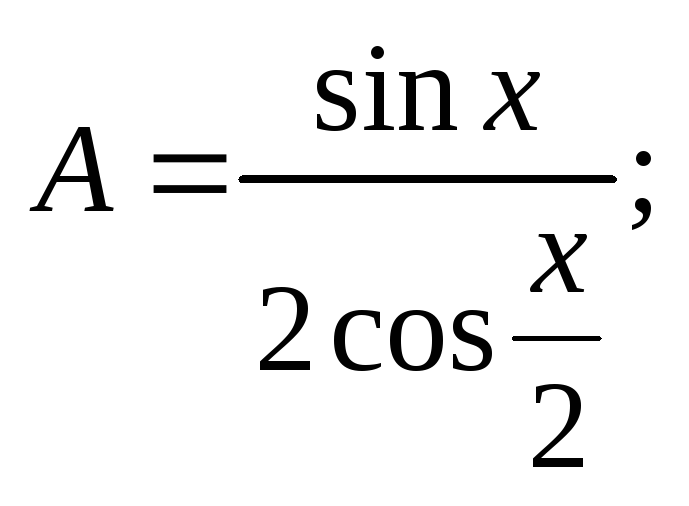
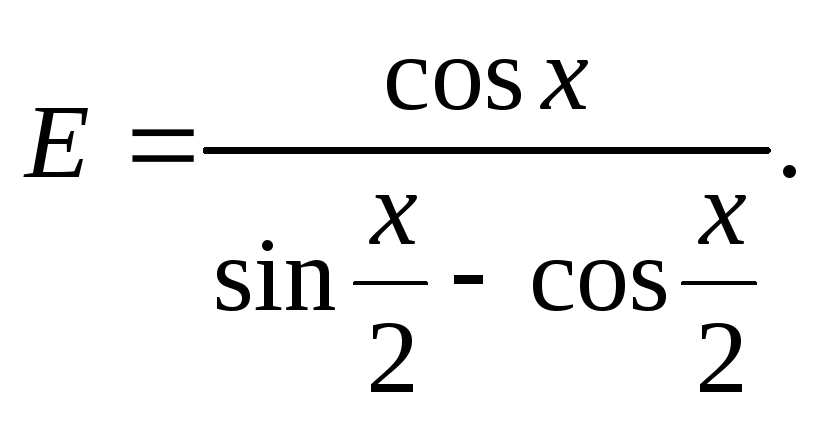
211)
Donner la valeur exacte des expressions suivantes :
212) Déterminer la période des fonctions suivantes :
a)
b)
c)
d)
213) Donner la représentions des fonctions suivantes :
a)
b)
c)
d)
214) Résoudre chaque équation dans l’intervalle donné.
a)
b)
c)
d)
e)
f)
215) Résoudre chaque équation dans l’intervalle donné.
a)
b)
c)
d)
e)
f)
216) Résoudre dans R les équations suivantes :
a)
b)
c)
d)
217) Résoudre dans R les équations suivantes :
a) (1 − 2 sin x)(tan 3x + 1) = 0; b) cos x cos 20° − sin x sin 20° = 1;
c) 2 sin 2x = 3 cos x; d) sin 2x + sin x = cos 2x + cos x;
e) 2 sin x
−
3
cos x = 2; e)
218)
Résoudre
dans R
l’équation
219)
Démontrer
que pour tout réel x
Résoudre
dans
les
équations : a)
b)
220) Résoudre chaque équation dans l’intervalle donné :
a)
sur
b)
sur
c)
sur
d)
sur
221)
Développer
En
déduire la résolution dans
de
222)
Donner
les solutions de l’équation
pour x appartenant à l’intervalle
223)
Résoudre dans R
l’équation
224)
Montrer
que pour tout réel x on a
Puis
en déduire que pour tout réel x on a
En
déduire la résolution dans R
de l’équation
225) Résoudre les équations suivantes :
a)
b)
c)
3.5 Inéquations trigonométriques
Méthode
1 Résoudre
les
inéquations
du
type
-
On trace un cercle trigonométrique et sur l’axe des abscisses, on place le point d’abscisse a. Sur cet axe, on détermine les points qui correspondent aux cosinus répondant à la condition.
-
Sur le cercle trigonométrique, on sélectionne les angles convenables.
-
On décrit l’ensemble des solutions.
E
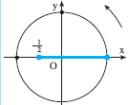
xemple :
résoudre
équivaut
à
a)
b) c)
k
Z
Réponse :
avec k entier relatif.
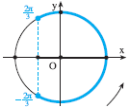
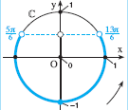
Exemple :
résoudre l’inéquation
a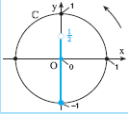
)
b) c)
Réponse :
avec k entier relatif.
Méthode
2
Résoudre les
inéquations
du
type
a) On trace un cercle trigonométrique et sur l’axe des tangentes, on place le point d’ordonnée a. Sur cet axe, on détermine les points qui correspondent aux tangentes répondant à la condition.
b) Sur le cercle trigonométrique, on sélectionne les angles convenables.
c) On décrit l’ensemble des solutions.
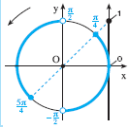
Exemple :
résoudre l’inéquation
a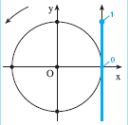
)
b) c)
Z
Réponse :
avec k entier relatif.
Remarque Pour résoudre d’autres inéquations trigonométriques, on se ramène à des inéquations élémentaires ou par des procédés analogiques à ceux utilisés pour résoudre des équations.