
- •Sommaire
- •4.3 Révision .............................................................................................72
- •1. Droites et plans de l’espace
- •1 .1 Règles de base
- •Exercices
- •1) Vrai ou faux ?
- •1.2 Positions relatives de deux droites
- •Exercices
- •1.3 Positions relatives d’une droite et d’un plan
- •Exercices
- •1.4 Positions relatives de deux plans
- •Exercices
- •1.5 Révision
- •2. Généralités sur les fonctions
- •2. 1 Notion de fonction
- •Exercices
- •2. 2 Étude de fonctions
- •2) Sens de variation d’une fonction
- •3) Maximum, minimum d’une fonction
- •4) Parité d’une fonction
- •Exercices
- •2. 3 Fonction « racine nième»
- •1) Représentation graphique
- •2) Sens de variation
- •Exercices
- •2.4 Révision
- •3. Fonctions trigonométriques
- •3. 1 Trigonométrie dans un triangle rectangle
- •Exercices
- •3. 2 Cosinus, sinus et tangente d’un nombre réel
- •2) Relation fondamentale de la trigonométrie:
- •6) Valeurs remarquables
- •8) Angles associés
- •Exercices
- •3.3 Fonctions trigonométriques
- •5) La représentation graphique 6) Les variations :
- •5) La représentation graphique 6) Les variations :
- •5) La représentation graphique 6) Les variations :
- •Exercices
- •3.4 Équations trigonométriques
- •Exercices
- •3.5 Inéquations trigonométriques
- •Exercices
- •3.6 Révision
- •4. Orthogonalité dans l’espace
- •4. 1 Droite et plan orthogonaux
- •6) Trois perpendiculaires
- •4) La projection orthogonale sur un plan
- •Exercices
- •4. 2 Plans perpendiculaires
- •Exercices
- •4.3 Révision
3.3 Fonctions trigonométriques
Mots à retenir
la fonction bornée (ограниченная функция) la périodicité (периодичность)
décaler de d vers le haut (vers le bas) (сместить на d вверх (вниз))
décaler de c vers la droite (vers le gauche) (сместить на c вправо (влево))
Définition : la fonction cosinus est la fonction qui à tout nombre réel x associe le nombre cos x.
Propriétés
1) L’ensemble de définition : la fonction cosinus est définie sur R.
2)
L’ensemble des images : x
étant un réel quelconque
![]() la
fonction cosinus est bornée.
la
fonction cosinus est bornée.
3) La
périodicité : la
fonction cosinus est périodique de période 2π, donc
![]() Il suffit que x décrive l’intervalle
Il suffit que x décrive l’intervalle
![]()
4) La parité : la fonction cosinus est paire et la représentation graphique est symétrique par rapport à l’axe des ordonnées dans un repère orthogonal.
5) La représentation graphique 6) Les variations :
|
x |
0
|
|
cos x |
0 0 |

Définition : la fonction sinus est la fonction qui tout nombre réel x associe le nombre sin x.
Propriétés
1) L’ensemble de définition : la fonction sinus est définie sur R.
2)
L’ensemble des images :
x étant un réel quelconque
![]() la
fonction sinus est bornée.
la
fonction sinus est bornée.
3) La
périodicité :
la fonction sinus est périodique de période 2π, donc
![]() Il suffit que x décrive l’intervalle
Il suffit que x décrive l’intervalle
![]()
4) La parité : la fonction sinus est impaire et la représentation graphique est symétrique par rapport à l’origine du repère.
5) La représentation graphique 6) Les variations :
-
x
0
 π
π
 2π
2πsin x

 1
1
0

 0 0
0 0-1
Définition :
la
fonction tangente est
la fonction qui à tout nombre réel différent de
![]() avec
k entier relatif, associe le nombre tan x.
avec
k entier relatif, associe le nombre tan x.
Propriétés
1)
L’ensemble de définition : la
fonction tangente n’est pas définie pour
![]()
2) L’ensemble des images : la fonction tangente peut prendre toutes les valeurs de R.
3) La
périodicité :
la fonction tangente est périodique de période π, donc si
![]()
![]() Il suffit que x décrive l’intervalle
Il suffit que x décrive l’intervalle
![]() ou
encore
ou
encore
![]()
4) La parité : la fonction tangente est impaire et la représentation graphique est symétrique par rapport à l’origine du repère.
5) La représentation graphique 6) Les variations :
-
x
0
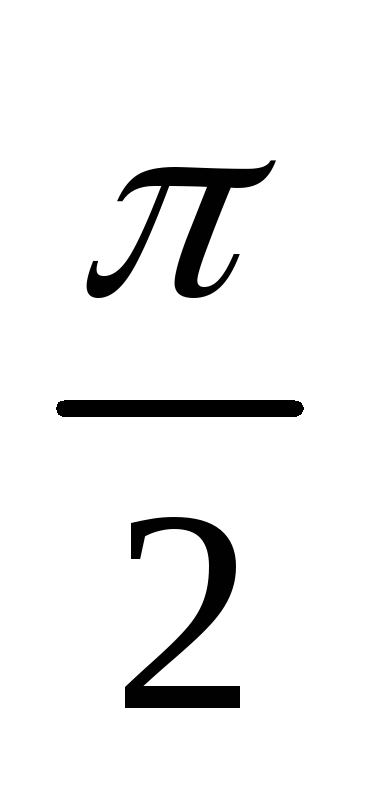 π
πtan x
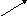


 0
0
0

La fonction tangente est croissante sur chacun
des intervalles.
Remarque
Les représentations graphiques des fonctions cosinus et sinus sont appelées sinusoïdes.
Méthodes
Une fonction sinusoïdale est donnée par la formule f(x) = a sin (bx + c) + d.
Dessiner les représentations graphiques des fonctions suivantes :
a) f (x) = sin 2x ; b) f (x) = 2sin x ; c) f (x) = 3sin x;
d )
f (x) = sin (x -
)
f (x) = sin (x -![]() )
; e) f (x) = sin
(2x
1);
f) f (x) =3
+ sin x.
)
; e) f (x) = sin
(2x
1);
f) f (x) =3
+ sin x.
a)
Par rapport
à f(x) = sin x,
la période
de
f (x) = sin 2x
est divisée par 2. D'une manière générale, la période de la
fonction f (x) = sin bx
est de![]()

b)
L'amplitude de f (x) = sin x est 2 (la fonction varie entre -1 et 1). L'amplitude de f (x) = 2sin x est 4 (la fonction varie entre -2 et 2). D'une manière générale, l'amplitude de la fonction f (x) = a sin x est 2a.
c )
)
L'amplitude de f (x) = 3sin x est de 6. Le signe « » provoque un « effet miroir » par rapport à l'axe des x.
d )
)
La courbe
de f (x) = sin (x
-![]() )
est décalée de
)
est décalée de
![]() vers
la droite. D'une manière générale, la fonction f (x) = sin(x
-
c)
(c>0)
est décalée de c
vers
la droite par rapport à f (x) = sin x.
vers
la droite. D'une manière générale, la fonction f (x) = sin(x
-
c)
(c>0)
est décalée de c
vers
la droite par rapport à f (x) = sin x.
f (x) = sin (x + c) (c > 0) est décalée de c vers la gauche par rapport à f (x) = sin x.

e)
D'une manière générale, f(x) = sin (bx + c)
« commence
» à
![]() .
Il en va de même pour les fonctions du type f (x) = a
sin (bx+c)
+ d.
.
Il en va de même pour les fonctions du type f (x) = a
sin (bx+c)
+ d.
Ci-dessus, avec b = 2 et c = 1, la fonction
f (x) = sin (2x1)
commence à
(x) = sin (2x1)
commence à
![]()
f)
Par rapport à f (x) = sin x, f (x) = 3 + sin x est décalée de 3 vers le haut. D'une manière générale, une fonction f (x) = sin x + d est décalée de d vers le haut (vers le bas si d est négatif).


 1
1
1
1
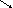
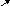 -1
-1