5. Тригонометрические подстановки
Интегралы вида
,
,
приводятся от рациональной относительно
и
функции с помощью тригонометрических
подстановок:
-
или
;
-
или
;
-
или
.
Пример 1. Найти интеграл
.
Решение
.
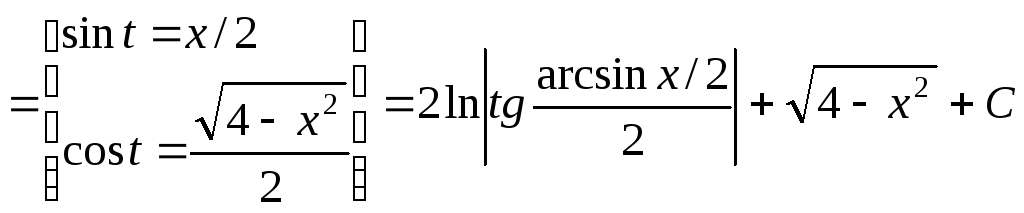Пример 2. Найти интеграл
.
Решение
.
Пример 3. Найти интеграл
.
Решение
.
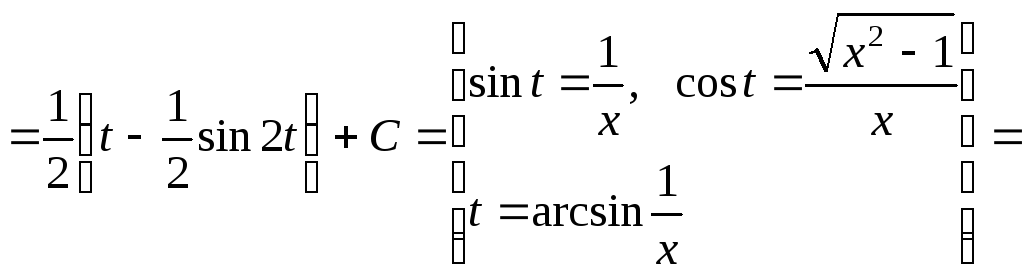
6. Интегралы вида
Интеграл
данного вида может быть преобразован
к интегралу вида
,
который был рассмотрен в п. 1.9.5.
Произведем преобразования трехчлена, стоящего под корнем:
.
Сделаем
замену переменной, положив
.
Тогда
.
Рассмотрим все возможные случаи.
-
Пусть
,
.
Введем обозначения
,
.
В этом случае будем иметь
.
-
Пусть
,
.
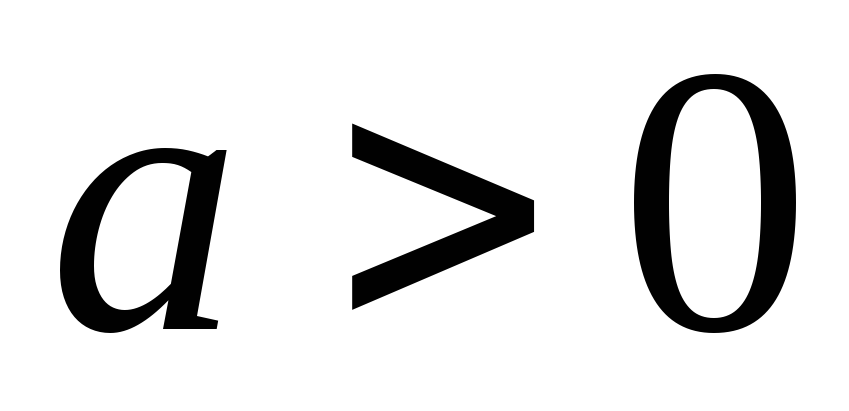Тогда
,
.
Следовательно,
.
-
Пусть
,
.
Тогда
,
.
Следовательно,
.
-
Пусть
,
.
В этом случае
есть комплексное число при любом x.
Таким образом, данный интеграл преобразуется к одному из следующих типов интегралов:
,
,
,
которые сводятся к интегралам, рассмотренным в п. 1.9.5.
Пример. Вычислить интеграл
.
Решение
Преобразуем подкоренное выражение, выделив полный квадрат:
,
т. е.
,
,
получили второй случай. Значит,
.
Выражение
соответствует третьему случаю
тригонометрических подстановок (см. п.
1.9.5). Выполним замену:
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
Возвращаясь к старой переменной с помощью формул
и
,
получим
.
Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
8.
(ответ:
).
9.
(ответ:
).
10.
(ответ:
).
11.
(ответ:
).
1.10. Функции, интегралы от которых не выражаются через элементарные функции
В
п. 1.1 отмечалось, что всякая функция
f(x),
непрерывная на интервале (a,
b),
имеет на этом интервале первообразную,
т. е. существует такая функция F(x),
что
Однако не всякая первообразная, даже
тогда, когда она существует, выражается
в конечном виде через элементарные
функции. Таковы первообразные, выраженные
интегралами
,
,
,
,
,
и многие другие.
Во
всех подобных случаях первообразная
представляет собой некоторую новую
функцию, которая не сводится к комбинации
конечного числа элементарных функций.
Так, например, та из первообразных
,
которая обращается в нуль при x
= 0, называется
функцией
Лапласа и
обозначается Ф(х).
Таким образом,
,
если Ф(0) = 0.
Эта функция хорошо изучена. Составлены подробные таблицы ее значений при различных значениях х.
Та
из первообразных
,
которая обращается в нуль при x
= 0, называется
эллиптическим
интегралом
и обозначается Е(х),
т. е.
,
если Е(0) = 0.
Для этой функции также составлены таблицы значений при различных значениях х.
2. Интеграл по мере области
2.1. Понятие интеграла по мере области
При решении многих задач физики, техники, математики требуется вычислить какие-то суммарные характеристики рассматриваемого объекта или процесса (часто говорят: «интегральные характеристики»). При этом характеристики объекта или процесса могут быть переменными: говорят, что локальные характеристики переменны и зависят от координат, времени. К таким задачам относятся, например, задачи отыскания площади, объема тел различной конфигурации, массы, моментов инерции тел, материал которых имеет различную плотность в различных точках, нахождения пути, пройденного материальной точкой при движении с изменяющейся скоростью, и т. д.
При решении таких задач используется общая математическая модель – интеграл по мере (или «интеграл по фигуре»).
Рассмотрим, как решается задача об отыскании массы тела, плотность которого в каждой точке известна и различна. Этим телом (фигурой) может быть:
-
прямолинейный стержень – l;
-
криволинейный стержень – L;
-
плоская пластина любой формы – D;
-
криволинейная поверхность – G;
-
тело, ограниченное любыми поверхностями, – V.
Чтобы обобщить эти объекты, будем говорить о фигуре G, обладающей некоторой массой. Пусть известна плотность распределения массы этой фигуры в каждой её точке Р
.
Так как масса – величина положительная, то необходимо считать эту функцию непрерывной и положительной на G.
Вычислим массу такой фигуры.
1.
Разобьем фигуру G
произвольным образом на непересекающиеся
части
.
Заметим, что при таком делении мы
используем метрическую характеристику:
-
в
– длина; -
в
– площадь; -
в
– объем.
Будем
обозначать эту характеристику
и назовём её мерой.
Меру можно представить как функцию множества
,
т. е.
множество
отображается на множество действительных
чисел.
Основные свойства меры:
а) неотрицательность
;
б) аддитивность
,
предполагается,
что
.
2.
В каждой части выберем произвольную
точку Pi
и предположим, что плотность массы
постоянна в пределах
и равна её значению в точке Pi,
т. е.
.
3.
Определим приближенное значение массы
части
.
4.
Масса (приближение) всей фигуры ищется
суммированием частичных масс
.
Выражение, стоящее справа, называется интегральной суммой.
5.
Для нахождения точного значения массы
переходим к пределу, устремив к нулю
наибольший из диаметров частей
.
Обозначим его
:
.
Тогда
.
Заметим,
что при
.
Если теперь отвлечься от конкретной задачи поиска массы, то можно составить интегральную сумму для некоторой непрерывной функции f(P), заданной на замкнутой, ограниченной фигуре G (можно говорить о замкнутой, ограниченной области, множестве). Это выражение вида
.
Рассмотрим
предел этих интегральных сумм при
Если этот предел не зависит ни от способа
разбиения фигуры на части
,
ни от выбора точек Pi
в каждой из частей, то его называют
интегралом
по мере
(по фигуре)
от функции f(P)
и обозначают
.
(2.1)
К
онкретизируем
введенные понятия для различных фигур.
I. Для отрезка [a, b] оси 0х (отрезок прямолинейного стержня, рис. 2.1)
(2.2)
− это обычный определенный интеграл.
Если
− линейная плотность материала стержня,
то (2.2) выражает его массу.
II. Для пространственной кривой l (рис. 2.2), т. е. G – это часть кривой, интеграл (2.1) принимает вид
.
(2.3)
Если
– функция линейной плотности массы, то
(2.3) определяет массу криволинейного
стержня.
Для плоской кривой выражение (2.3) немного упрощается:
.
(2.4)
Интегралы (2.3) и (2.4) называются криволинейными интегралами по длине дуги, или криволинейными интегралами I рода.
III. В пространстве R2 в качестве фигуры имеем ограниченную часть плоскости – область D (рис. 2.3). Тогда
,
.
Интеграл (2.1) принимает вид
,
(2.5)
где
di
– диаметр
.
Интеграл (2.5) называется двойным интегралом по области D.
Если
– функция плотности массы, то (2.5) выражает
массу неоднородной пластины.
IV. Для поверхности Q, где
,
,
интеграл (2.1) принимает вид
(2.6)
и
называется поверхностным
интегралом по площади поверхности.
Если
– функция поверхностной плотности
массы, то (2.6) выражает массу поверхности
Q.
V. Для пространственного тела Т (рис. 2.4), где
,
,
интеграл (2.1) принимает вид
(2.7)
и называется тройным интегралом по области Т.
Если
− функция объемной плотности массы, то
(2.7) выражает массу тела Т.