2.4.2. Формула трапеций
Формула
трапеций аналогична формулам
прямоугольников, но f(x)
заменяется на каждом отрезке длиной
линейной функцией, а площадь – суммой
площадей трапеций (рис. 2.9).
Рис. 2.9
Формулу трапеций можно получить как среднее арифметическое формул прямоугольников.
Формула трапеций точнее, чем формулы прямоугольников; объём вычислений остаётся почти таким же.
2.4.3. Формула парабол (Симпсона)
Формула
парабол, предложенная английским
математиком Симпсоном, основана на
замене функции f(x)
на отрезках длиной
дугой параболы (рис. 2.10).
Рис. 2.10
Разобьем
отрезок
на четное число 2n
равных отрезков
.
Через
каждые 3 точки
проводится дуга параболы
.
Таким образом, на участке
кривая f(x)
заменяется параболой. Мы осуществили
кусочно квадратичную аппроксимацию.
Площадь, ограниченную одной из парабол,
нетрудно подсчитать:
.
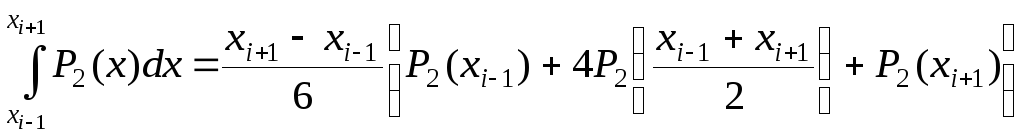Суммируя эти площади, в результате найдем приближенное значение интеграла
.
Заданная точность вычисления достигается за значительно меньшее число операций.
Пример.
Вычислить
интеграл
.
Решение
Функция f(x) является непрерывной на всей числовой оси, однако ее первообразная не выражается через элементарные функции, т. е. данный интеграл не может быть вычислен. Поэтому применим методы приближенного вычисления и найдем значение определенного интеграла с помощью всех представленных методов.
Разобьем
отрезок
на 10 равных частей. Тогда
.
Составим таблицу значений подынтегральной функции (табл. 2.1).
Таблица 2.1
|
x |
|
|
0 |
1 |
|
0,1 |
1,01005 |
|
0,2 |
1,040811 |
|
0,3 |
1,094174 |
|
0,4 |
1,173511 |
|
0,5 |
1,284025 |
|
0,6 |
1,433329 |
|
0,7 |
1,632316 |
|
0,8 |
1,896481 |
|
0,9 |
2,247908 |
|
1 |
2,718282 |
По первой формуле прямоугольников получим
.
По второй формуле прямоугольников получим
.
В данном случае первая формула дает значение интеграла с «недостатком», а вторая – с «избытком».
По формуле трапеций получим
.
По формуле Симпсона имеем
Как мы видим, результаты вычислений сильно различаются. Погрешность вычислений можно оценить, если увеличить число разбиения n.
Для того чтобы знать, сколько точек деления надо взять, чтобы подсчитать интеграл с заданной степенью точности, можно воспользоваться формулами оценки погрешности, получающейся при приближенном вычислении интеграла. В данном курсе мы не приводим этих оценок.
Данный
интеграл можно вычислить, если
воспользоваться формулами разложения
функции
в ряд (подробно этот материал будет
разобран в следующем учебном пособии
«Ряды» данной серии). В разложении
заменим
x
на
и, учитывая, что данный ряд сходится при
,
проинтегрируем полученный ряд почленно,
используя свойства степенных рядов:
.
Как видно, результат совпадает с ответами, полученными по формулам трапеций и Симпсона, с точностью двух знаков, а ответ, полученный с помощью формул прямоугольников, дает слишком приблизительное значение. Какое количество членов ряда надо взять для достижения необходимой точности результата, полученного с помощью формулы разложения функции в ряд, будет разобрано в следующем учебном пособии «Ряды» данной серии.