9.3. Механические приложения кратных интегралов

Пусть в пространстве R³ задано тело T с элементом объема dV (рис. 9.13). Тогда масса этого элемента может быть вычислена по формуле

,

де – функция плотности. Тогда вся масса тела

.

Рис. 9.13

Элементарный статический момент относительно плоскости хOу

.

Момент всего тела относительно плоскости х0у

.

Аналогично находятся моменты относительно других плоскостей:

,

.

Из механики известны формулы для вычисления координат центра тяжести тела

где m – масса тела; – статические моменты относительно плоскостей координат. Тогда

.

Аналогично вычисляются и .

Моменты инерции относительно осей координат соответственно равны:

,

,

.

Пример 1. Найти координаты центра тяжести тела, ограниченного плоскостями .

Решение

Найдем массу рассматриваемого тела

.

Тогда

;

;

.

Пример 2. Вычислить момент инерции фигуры, ограниченной кардиоидой , относительно оси Oх.

Решение

Перейдя к полярным координатам в формуле и полагая , получим

.

Задания для самостоятельного решения

1. Запишите координаты центра тяжести пластины, стержня.

2. Найти массу дуги окружности , ), если ее линейная плотность равна y (ответ: 2).

3. Найти массу фигуры, ограниченной линиями , (ответ: 8).

4. Определить координаты центра тяжести фигуры, ограниченной линиями , , , (ответ: ).

5. Найти массу куба , , , если плотность тела (ответ: 24).

6. Найти координаты центра тяжести тела, ограниченного поверхностями , , , , (ответ: ).

9.4. Примеры физических приложений определённых интегралов

1. Масса неоднородного стержня с линейной плотностью (рис. 9.14) вычисляется по формуле

Рис. 9.14

2. Заряд, распределенный вдоль диэлектрического стержня с линейной плотностью q(x), вычисляется аналогично массе неоднородного стержня

3. Количество тепла, сосредоточенного в неравномерно нагретом стержне, вычисляется столь же просто:

где с – удельная теплоёмкость единицы массы; s – площадь сечения стержня (s = const); γ – плотность массы материала стержня; Т – температура.

Подумайте, что изменится, если s = s(x).

4. Работа А упругого элемента (пружины) при растяжении из свободного состояния, когда конец элемента имеет абсциссу x = 0, до того положения, когда его конец будет иметь абсциссу x = h (рис. 9.15), вычисляется следующим образом.

Сила F, уравновешивающая растянутый упругий элемент, равна cx: F = cx, где с – жесткость пружины (положим для простоты с = const).

Тогда

Подумайте, каков геометрический смысл связи графиков силы F(x) и работы A(x).

Пример 1. Какую работу надо затратить, чтобы тело массы т поднять с поверхности Земли, радиус которой R, на высоту h? Чему равна эта работа, если тело должно быть удалено на бесконечность?

Решение

Если переменная сила действует в направлении оси Ох, то на отрезке работа силы

.

Сила, действующая на тело массы т, равна , где r – расстояние от центра Земли. Если радиус Земли R, то работа, затрачиваемая на поднятие массы т с поверхности Земли до высоты , вычисляется по формуле

.

На поверхности Земли , поэтому и

,

, или .

Пример 2. По катушке с индуктивностью L = 60 Гн течет постоянный ток I = 5 А. Найти энергию W магнитного поля катушки.

Решение

Из курса физики известно, что проводник с индуктивностью L, по которому течет ток силы I, обладает энергией , которая локализована в возбужденном током магнитном поле. Следовательно, поле будет иметь энергию

Дж.

Пример 3. Котел имеет форму параболоида вращения (рис. 9.16). Радиус основания R, глубина котла Н. Он наполнен жидкостью, плотность которой d. Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.

Решение

Разбиваем объем параболоида плоскостями, перпендикулярными оси вращения, на слои толщины dx (на чертеже одно из таких сечений отмечено штриховкой). Вес слоя жидкости, расположенного на расстоянии х от вершины, равен (с точностью до бесконечно малых высшего порядка), а работа по перемещению этого слоя на высоту равна . Следовательно, искомая работа

.

Уравнение параболы, вращением которой вокруг оси Ох получен рассматриваемый параболоид, имеет вид . Параметр р находим из условия . Отсюда и, значит, .

Подставляя полученное значение y² в подынтегральное выражение, имеем

.

Пример 4. Найти силу давления, испытываемую полукругом радиуса r, погруженным вертикально в воду так, что его диаметр совпадает с поверхностью воды (рис. 9.17).

Решение

Для вычисления силы давления жидкости используют закон Паскаля, согласно которому

,

где Р – сила давления жидкости на площадку S, – плотность жидкости, h – глубина погружения, g – ускорение силы тяжести.

Разбиваем площадь полукруга на элементы – полоски, параллельные поверхности воды. Площадь одного такого элемента (отбрасывая бесконечно малую высшего порядка), находящегося на расстоянии h от поверхности,

Сила давления, испытываемая этим элементом,

Отсюда сила давления на весь полукруг есть

Пример 5. Изменение производительности некоторого производства с течением времени от начала внедрения нового технологического процесса задается функцией , где t – время в месяцах. Найти объем продукции, произведенной:

а) за первый месяц;

б) за третий месяц;

в) за шестой месяц;

г) за последний месяц года, считая от начала внедрения рассматриваемого технологического процесса.

Решение

Пусть функция описывает изменение производительности некоторого производства с течением времени. Тогда объем продукции , произведенной за промежуток времени , вычисляется по следующей формуле:

.

Тогда

;

;

;

.

Сравнивая между собой полученные результаты, можно заметить, что основная работа по внедрению данного технологического процесса приходится на первую половину года.

Пример 6. Найти объем выпускаемой продукции за пять лет, если функции Кобба – Дугласа , , , , , (t – время в годах).

Решение

Возможность учета влияния различных факторов на изменения производительности производства связана с использованием, например, так называемых функций Кобба – Дугласа. В этом случае производительность f(t) представляется в виде произведения

,

где функции A(t), L(t), K(t) есть величины затрат природных pecурсов, труда и капитала (соответственно), a₀, , , – некоторые числа.

Подставляя функцию производительности f(t), получим

Применяем дважды последовательно формулу интегрирования по частям:

Пример 7. По данным исследований о распределении доходов в одной из стран, кривая Лоренца может быть описана уравнением , где . Вычислить коэффициент Джини k.

Решение

Рассмотрим функцию , характеризующую неравномерность распределения доходов среди населения, где у – доля совокупного дохода, получаемого долей х беднейшего населения. График этой функции называется кривой Лоренца (рис. 9.18). Очевидно, что при , и неравномерность распределения доходов тем больше, чем больше площадь фигуры ОАВ (см. рис. 9.18). Поэтому в качестве меры указанной неравномерности используют так называемый коэффициент Джини k, равный отношению площади фигуры ОАВ к площади треугольника ОАС.

Тогда

.

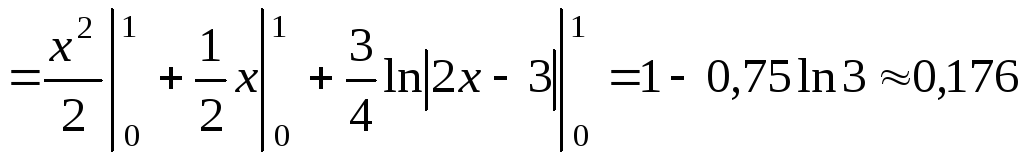Тогда

.

Пример 8. Найти выигрыши потребителей и поставщиков в предложении установления рыночного равновесия, если законы спроса и предложения имеют вид

, .

Решение

Пусть – кривая спроса D на некоторый товар и – кривая предложения S, где р – цена на товар, х – величина спроса (предложения). Обозначим через точку рыночного равновесия (см. рис. 9.19).

Доход от реализации количества товара по равновесной цене равен произведению . Если предполагать непрерывное снижение цены от максимальной до равновесной p₀ по мере удовлетворения спроса, то доход составит . Величина денежных средств сберегается потребителями, если предполагать продажу товара по равновесной цене p₀, поэтому С называется также выигрышем потребителей.

Аналогично

называется выигрышем поставщиков.

Величины С и Р численно равны площадям соответствующих криволинейных треугольников (рис. 9.19).

Решая систему

найдем точку рыночного равновесия: , .

Тогда

(ден. ед.),

(ден. ед.).

Пример 9. По данным исследований в распределении доходов в одной из стран, кривая Лоренца ОВА (рис. 9.18) может быть описана уравнением , где х – доля населения, у – доля доходов населения. Вычислить коэффициент Джини.

Решение

Очевидно, коэффициент Джини (см. рис. 9.18)

, так как .

.

Поэтому .

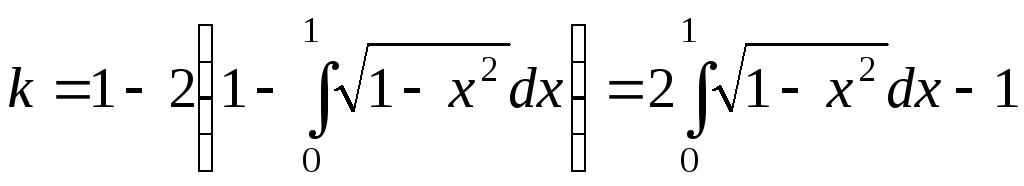С помощью замены, например, можно вычислить . Итак, коэффициент Джини .

Достаточно высокое значение k показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.

Пример 10. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млрд руб. и намечается ежегодно увеличивать капиталовложения на 1 млрд руб.

Решение

Определение начальной суммы по ее конечной величине, поденной через время t (лет) при годовом проценте (процентной ставке) р, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.

Пусть – конечная сумма, полученная за t лет, и К – дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то , где – удельная процентная ставка. Тогда . В случае сложных процентов и потому .

Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) и при удельной норме процента, равной i, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход К за время Т вычисляется по формуле

.

Очевидно, что капиталовложения задаются функцией . Тогда дисконтированная сумма капиталовложений

.

Интегрируя по частям, получим K = 30 млрд руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд руб. равносильны одновременным первоначальным вложениям 30,5 млрд руб. при той же начисляемой непрерывной процентной ставке.

Пример 11. Найти среднее время, затраченное на освоение одного изделия в период освоения от x₁ = 100 до x₂ = 121 изделий, полагая a = 600 (мин), b = 0,5.

Решение

Пусть известна функция t = t(x), описывающая изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где х – порядковый номер изделия в партии. Тогда среднее время t_cp , затраченное на изготовление одного изделия в период освоения от x₁ до х₂ изделий, вычисляется по теореме о среднем

.

Что касается функции изменения затрат времени на изготовление изделий t = t(x), то часто она имеет вид

,

где а – затраты времени на первое изделие, b – показатель производственного процесса. Тогда

(мин).