Задания для самостоятельного решения

1. Покажите, что криволинейный интеграл первого рода есть линейный функционал.

2. Подумайте, какой геометрический смысл можно придать криволинейному интегралу первого рода, если

3. Вычислите криволинейные интегралы:

а)

б)

в)

(ответ: а) ; б) ; в) ).

8.2. Криволинейные интегралы по координатам

8.2.1. Понятие о векторном поле

Если каждой точке М некоторого пространства поставлен в соответствие вектор длина и направление которого зависят от точки пространства, то говорят, что в этом пространстве задано векторное поле.

Таким образом, векторное поле – это вектор-функция где Если – координаты в то

или

Векторное поле называется плоским, если R = 0, а функции P и Q не зависят от z , т. е.

Примерами векторных полей являются поле скоростей жидкости, поле сил тяготения, поле электрической и магнитной напряженности.

Представим себе линию, касательные к которой в каждой точке М совпадают с векторами в этой точке. Эта кривая является огибающей векторного поля , и её называют векторной линией (рис. 8.3).

Рассмотрим элемент дуги векторной линии (рис. 8.4)

.

При вектор Δ по направлению будет стремиться к касательной. Поэтому можно говорить об ориентированном элементе дуги кривой l

.

Так как он направлен по касательной, то

.

Условие коллинеарности может быть записано в виде

. (8.8)

Тогда

Получили дифференциальные уравнения векторной линии. Решением этой системы будут параметрические уравнения

В гидродинамике это линии тока, в электротехнике – силовые линии.

Пример. Дано векторное поле

.

Найти уравнения векторных линий.

Решение

Составим дифференциальное уравнение из условия коллинеарности (8.8):

,

тогда

.

Семейство векторных линий изображено на рис. 8.5.

8.2.2. Определение криволинейного интеграла по координатам

Гладкую кривую подобно прямой линии можно ориентировать, задав на ней направление. Такие кривые называются ориентированными (рис. 8.6).

Пусть задано векторное поле

и некоторая ориентированная кривая l, гладкая между точками А и В. Элемент дуги этой кривой

.

Он является ориентированным элементом дуги. Следовательно, dx, dy, dz могут рассматриваться как проекции на соответствующие оси. Тогда они имеют собственный знак

,

,

.

Образуем скалярное произведение

.

Тогда выражение

(8.9)

называется криволинейным интегралом по координатам, или криволинейным интегралом II рода.

В отличие от криволинейного интеграла I рода, в данном интеграле играет роль направление, заданное на кривой, поэтому будет справедливо свойство

.

Остальные свойства криволинейного интеграла II рода не отличаются от свойств интеграла по мере.

8.2.3. Вычисление криволинейного интеграла по координатам

Рассмотрим, как вычисляется криволинейный интеграл II рода.

1. Пусть кривая L задана параметрически

Подставляя эти соотношения в (8.9), получим

где t_A и t_B − параметры начальной А и конечной В точек интегрирования.

Если кривая L плоская, то формула вычисления упрощается:

.

2. Пусть кривая L – плоская и задана уравнением . Можно считать, что она задана параметрически, введя промежуточный параметр t

и применить предыдущую формулу для случая плоской кривой, а затем заменить t на х. Получим

.

Пример 1. Вычислить криволинейный интеграл вдоль дуги кубической параболы от точки А(1; 1) до В(2; 8).

Решение

Пример 2. Вычислить криволинейный интеграл вдоль кривой от точки А(1; 1) до точки В(2; 16).

Решение

Пример 3. Вычислить интеграл вдоль верхней половины окружности от точки А(-1; 0) до точки В(0; 1).

Решение

Запишем уравнение окружности в параметрическом виде: Учитывая заданное направление обхода, получаем

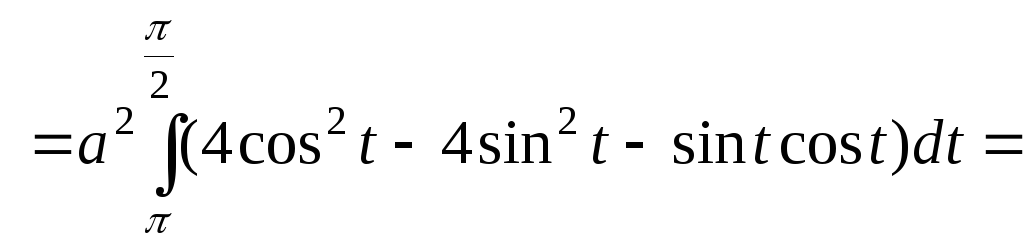
Если P, Q, R – проекции силы на координатные оси и то

Таким образом, криволинейный интеграл по координатам выражает работу силы , затрачиваемую на перемещение объекта вдоль кривой L (рис. 8.7).

Криволинейный интеграл II рода по замкнутому контуру L называется циркуляцией векторного поля по этому контуру

Ориентация замкнутого контура L считается положительной в правой системе координат, если область, лежащая внутри L, остается слева по отношению к движущейся по контуру L точке.