Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
1).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
8.
(ответ:
0).
2.3.2. Вычисление определённых интегралов с помощью подстановки
Теорема.
Если
С
,
причём функция
отображает отрезок
на отрезок
,
то
Доказательство
Пусть F(x) – первообразная для f(x), тогда
.
С другой стороны,
.
При вычислении определённого интеграла с помощью подстановки возвращаться к прежней переменной интегрирования не нужно. Однако не следует забывать о необходимости изменения пределов интегрирования.
Пример
1. Вычислить
.
Решение
Применим
подстановку
.
Выразим
.
Найдем новые пределы интегрирования
Получим
.
Пример
2. Вычислить
.
Решение
Применим
подстановку
,
тогда
.
Найдем новые пределы интегрирования
Получим
.
Пример
3. Вычислить
.
Решение
Пусть
,
тогда
.
Новые пределы интегрирования
.
Пример 4. Вычислить площадь эллипса
Решение
Очевидно, что искомая площадь
С помощью подстановки
получаем
=
(кв. ед.)
2.3.3. Вычисление определённых интегралов путём интегрирования по частям
Формула интегрирования по частям для определённого интеграла выводится очень просто.
Пусть
.
Тогда
т. е.
Пример
1. Вычислить
.
Решение
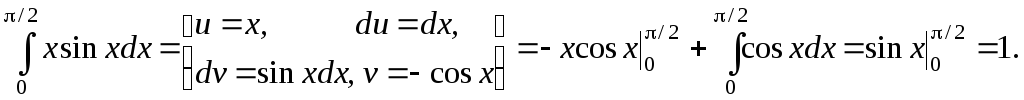
Пример
2. Вычислить
.
Решение
Применим формулу интегрирования по частям
.
Пример
3. Вычислить
.
Решение
.
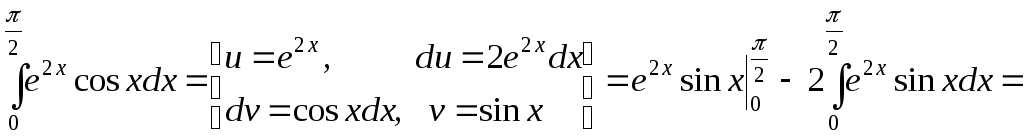
Получили
уравнение относительно интеграла
.
Решив его, получим
.
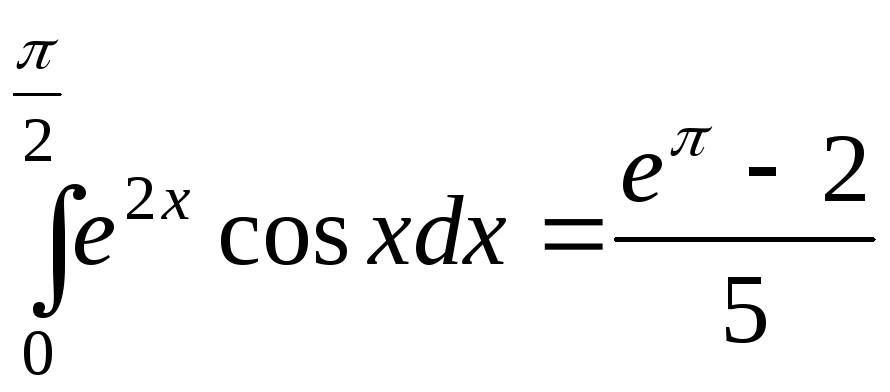2.4. Приближенное вычисление определённых интегралов. Понятие о численном интегрировании
Пусть требуется вычислить определённый интеграл
от непрерывной функции f(x). Если может быть найдена первообразная F(x) подынтегральной функции f(x), то интеграл может быть вычислен по формуле Ньютона – Лейбница
.
Если же первообразная не может быть найдена или если f(x) задана графически или таблично, то для вычисления интеграла прибегают к приближенным формулам, точность которых может быть сделана сколь угодно большой.
Приближенные
методы вычисления определенного
интеграла в большинстве случаев основаны
на том, что определенный интеграл
численно равен площади криволинейной
трапеции, ограниченной кривой y
= f(x),
отрезком
оси 0х
и вертикальными прямыми x
= a,
x
= b.
Благодаря этому задача о приближенном
вычислении интеграла равносильна задаче
о приближенном вычислении площади
криволинейной трапеции. При этом кривая
y = f(x)
заменяется новой кривой, которая
достаточно «близка» к данной. Тогда
искомая площадь приближенно равна
площади криволинейной трапеции,
ограниченной новой кривой.
В качестве этой кривой выбирают такую, для которой площадь криволинейной трапеции подсчитывается просто. В зависимости от выбора новой кривой (метода аппроксимации) мы получаем ту или иную приближенную формулу, часто называемую квадратурной.
2.4.1. Формула прямоугольников
Формула прямоугольников основана на замене подынтегральной функции f(x) на кусочно-постоянную функцию.
Отрезок
разбивается на n
частей равной длины
.
На каждой из частей
функция f(x)
заменяется постоянной величиной
.
Тогда площадь криволинейной трапеции
приближенно приравнивается к площади
ступенчатой фигуры, составленной из
прямоугольников (рис. 2.8).
Рис. 2.8
Тогда
– для случая вписанной ступенчатой фигуры (штриховка)
;
– для случая описанной ступенчатой фигуры (пунктир)
Для
повышения точности (уменьшения ошибки
вычисления) требуется увеличивать n
– число элементов разбиения отрезка
на части. При этом резко возрастает
количество вычислений.