Задания для самостоятельного решения

1. Подумайте, что выражает интеграл 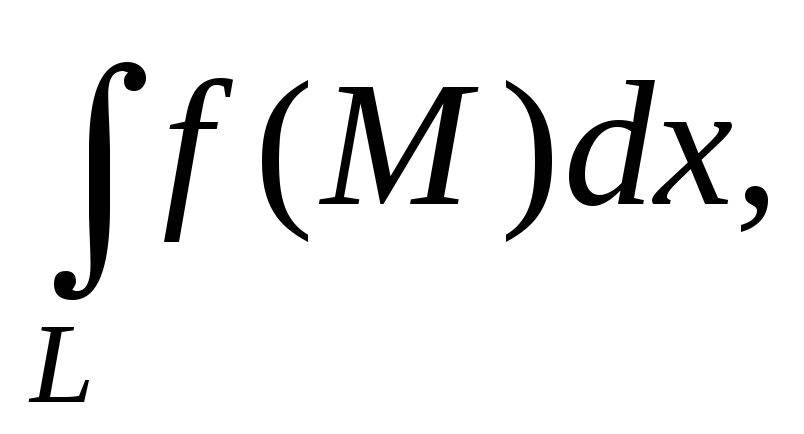если

2. Вычислите криволинейные интегралы:

а) где L – дуга параболы от А(-1; 1) до В(-2; 4);

б) вдоль ломаной, соединяющей точки О(0; 0), А(2; 0) и В(4; 2);

в) , если ;

г) вдоль прямой, соединяющей точки А(1; 2; -−1) и В(3; 3; 2) (ответ: а) ; б) ; в) ; г) ).

3. Вычислите работу силы при перемещении материальной точки вдоль верхней половины эллипса из точки А(а; 0) в точку В(−а; 0) (ответ: ).

8.2.4. Формула Грина

Формула Грина устанавливает связь между криволинейным интегралом по границе L плоской области D и двойным интегралом по этой области.

Теорема. Пусть D – правильная область, а функции непрерывны вместе со своими производными и в замкнутой области Тогда имеет место формула Грина

(8.10)

Доказательство

Пусть задана область D (рис. 8.8). Рассмотрим интеграл

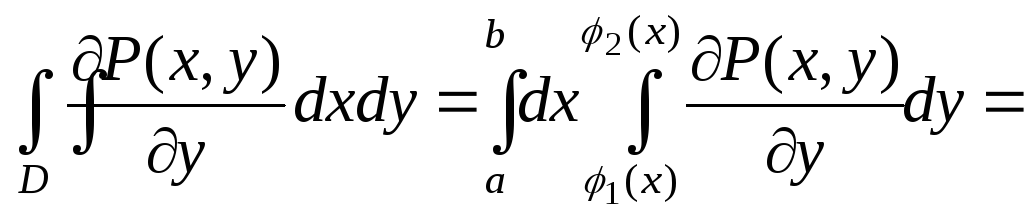
Таким образом,

Аналогично доказывается, что

Из двух последних равенств следует формула (8.10).

Формула Грина справедлива и для двусвязной области D (рис. 8.9), Действительно, область D можно превратить в односвязную, проведя так называемый разрез, т. е. соединив наружный и внутренний контуры некоторой линией и исключив ее из области. При этом двойной интеграл не изменится, а криволинейный интеграл вдоль разреза обращается в нуль, так как разрез при обходе односвязной области проходится в противоположных направлениях.

8.2.5. Независимость криволинейного интеграла от формы кривой интегрирования

Рассмотрим случай плоской кривой. Две точки А и В – начало и конец пути интегрирования – могут быть соединены различными кривыми: L₁ и L₂ (рис. 8.10).

По каждой из этих кривых, если это возможно, проведем интегрирование. Может случиться, что заданное векторное поле обладает таким свойством, при котором результаты интегрирования не будут зависеть от выбора кривой.

Установим это условие. Пусть

Тогда

т. е. циркуляция Ц = 0 для Справедливы рассуждения и в обратном порядке. Мы пришли к следующему утверждению.

Теорема 1. Для независимости криволинейного интеграла от формы кривой интегрирования необходимо и достаточно, чтобы циркуляция векторного поля была равна нулю по любому замкнутому контуру L.

Это условие неконструктивно. Существует другое условие.

Теорема 2. Для независимости криволинейного интеграла от формы кривой интегрирования необходимо и достаточно, чтобы выражение являлось полным дифференциалом некоторой функции U(x, y), т. е.

.

Доказательство

1.  Достаточность. Пусть , т. е. является полным дифференциалом. Если P и Q − дифференцируемые функции, то

(условие полного дифференциала).

Используя формулу Грина, получим

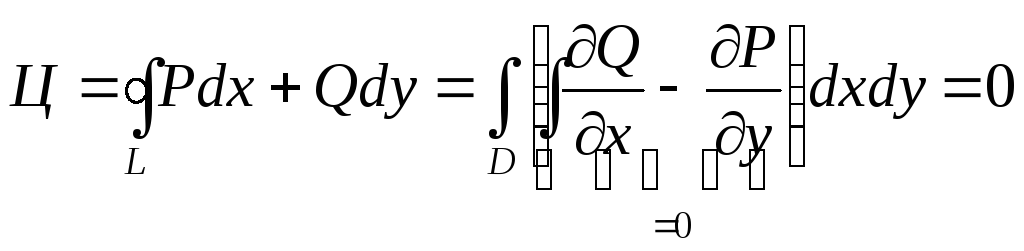, т. е. .

2. Необходимость. Пусть не зависят от L. Это означает, что , т. е.

.

Тогда по формуле Грина

, (8.11)

откуда

или .

Замечание. При доказательстве (8.11) использовали лемму:

если и , то f (x,y) = 0.

Из доказанной теоремы вытекает следствие.

Следствие. Если криволинейный интеграл не зависит от формы кривой интегрирования, то

Функцию u(x, y) называют силовой, или потенциальной, а величину – потенциалом.

Тогда

. (8.12)

Вспомним физический смысл скалярного произведения, которое стоит под интегралом в левой части последнего равенства. Это элементарная работа поля на участке кривой L

,

тогда интеграл от этой элементарной работы по кривой L от А до В даст работу поля на кривой АВ. Соотношение (8.12) означает, что работа равна разности потенциалов начала и конца пути и не зависит от формы этого пути.

Заметим теперь, что

,

т. е. если векторное поле является градиентом некоторого скалярного поля, то криволинейный интеграл не зависит от формы кривой интегрирования. Такие векторные поля называются потенциальными (поле сил тяготения).

Пример. Применяя формулу Грина, вычислить интеграл , где L – окружность , пробегаемая против хода часовой стрелки.

Решение

Здесь , . Тогда . Следовательно,

.

Введем полярные координаты . Значит,

.