3.3. Теоремы о сходимости несобственных интегралов

Вопрос о сходимости несобственного интеграла в ряде случаев можно решить без его вычисления. Это особенно важно, когда первообразную через элементарные функции в конечном виде выразить невозможно. Рассмотрим простейшие теоремы относительно сходимости несобственных интегралов с бесконечными пределами.

Теорема 1. Если и интеграл сходится, то сходится и интеграл Если при тех же предположениях интеграл расходится, то расходится и интеграл .

Доказательство

Е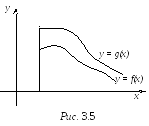сли существует, то представляет величину ограниченную и монотонно возрастающую. Так как , значит, и площадь, ограниченная этой кривой, меньше, чем площадь под кривой g(x) (рис. 3.5). Значит, существует и .

Вторая часть теоремы доказывается аналогично.

Теорема 2. Если сходится интеграл то сходится и интеграл .

Не приводя доказательства этой теоремы, заметим, что в первом интеграле суммируются площади, лежащие над и под осью абсцисс, а во втором интеграле площади под осью абсцисс учитываются со знаком минус (рис. 3.6). Поэтому первый интеграл сходится «труднее»: он может расходиться в тех случаях, когда второй интеграл сходится.

Если интеграл сходится, то интеграл называется абсолютно сходящимся.

Если интеграл сходится, а расходится, то первый интеграл называется условно сходящимся.

Теорема 3. Если и существует конечный ненулевой предел то интегралы , либо оба сходятся, либо оба расходятся.

Доказательство этой теоремы не приводим.

Наиболее часто при выяснении вопроса о сходимости несобственного интеграла выполняют сравнение его с интегралом от степенной функции

(3.6)

который сходится при p > 1 и расходится при p

Действительно,

Пример 1. Определить, сходится ли интеграл

Решение

(см. (3.6)).

Следовательно, данный интеграл сходится, причем абсолютно.

Пример 2. Исследовать на сходимость интеграл

.

Решение

Сравним подынтегральную функцию с

.

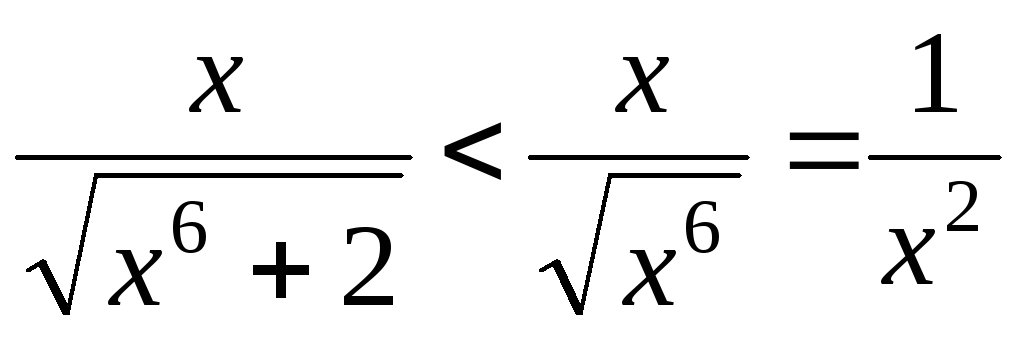По формуле (3.6) несобственный интеграл сходится . Таким образом, данный интеграл сходится.

Ответ: Интеграл сходится.

Пример 3. Исследовать на сходимость

.

Решение

Преобразуем подынтегральную функцию

.

Несобственный интеграл от функции сходится . Найдем

.

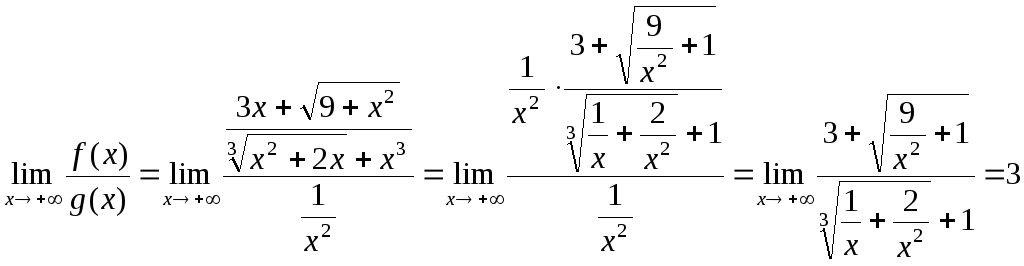Используя теорему 3, получаем, что данный несобственный интеграл сходится.

Ответ: Интеграл сходится.

Теоремы, аналогично рассмотренным, справедливы и для несобственных интегралов от разрывных функций (сформулируйте их самостоятельно). При этом сравнение часто осуществляют с интегралами со степенной особенностью

и ,

которые сходятся при p < 1 и расходятся при p 1 (проверить самостоятельно).

Пример 4. Исследовать на сходимость интеграл

.

Решение

Подынтегральная функция является бесконечно большой при . Представим ее в виде

.

Найдем

,

т. е. предел конечен и не равен нулю. Значит, интегралы и ведут себя одинаково. Интеграл сходится, так как . Следовательно, и исходный интеграл тоже сходится.

Ответ: Интеграл сходится.

Пример 5. Исследовать на сходимость интеграл

.

Решение

Подынтегральная функция f(x) в промежутке интегрирования положительна и при . Пользуясь теоремой об эквивалентных бесконечно малых, преобразуем числитель и знаменатель подынтегральной дроби:

при ,

тогда

.

Следовательно,

при .

Интеграл сходится, так как . Следовательно, и исходный интеграл тоже сходится.

Ответ: Интеграл сходится.