1.7.2. Интегрирование рациональных дробей с помощью разложения на простейшие дроби

Интегрирование рациональной дроби проводится по следующему алгоритму:

1. если дана неправильная рациональная дробь, то необходимо выделить из нее целую часть, т. е. представить в виде

,

где M(x) – многочлен, а – правильная рациональная дробь;

2) разложить знаменатель дроби на линейные и квадратичные множители:

,

где , т. е. трехчлен имеет комплексные сопряженные корни;

3) правильную рациональную дробь разложить на простейшие дроби:

4) вычислить неопределенные коэффициенты . Для этого привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения.

В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.

Случай 1. Знаменатель имеет только действительные различные корни.

Пример. Вычислить интеграл

.

Решение

Рассмотрим подынтегральную функцию – правильная рациональная дробь. Представим ее в виде суммы простейших дробей, разложив знаменатель на множители:

;

.

Приведем к общему знаменателю и рассмотрим числители дробей

.

Полагая, что , найдем , т. е. . Если , то получим , т. е. . При получим , т. е. .

Итак,

.

Случай 2. Знаменатель имеет только действительные корни, причем некоторые из них – кратные.

Пример. Вычислить интеграл

.

Решение

Рассмотрим подынтегральную функцию – правильная рациональная дробь. Представим ее в виде суммы простейших дробей. Корни знаменателя – действительные числа, среди них есть кратные (выражению соответствует сумма трех простейших дробей).

Таким образом,

.

Приведем к общему знаменателю и рассмотрим числители дробей:

.

Сравним коэффициенты при одинаковых степенях x:

Решая полученную систему уравнений, находим неизвестные коэффициенты

.

Итак,

.

Случай 3. Среди корней имеются простые комплексные корни.

Пример 1. Вычислить интеграл

.

Решение

Рассмотрим подынтегральную функцию – неправильная рациональная дробь. Выделим целую часть

.

Представим дробь в виде суммы простейших дробей, разложив знаменатель на множители

.

Тогда

.

Приведем к общему знаменателю и рассмотрим числители дробей

.

Сравним коэффициенты при одинаковых степенях x:

Итак,

.

Пример 2. Найти интеграл

Решение

Рассмотрим подынтегральную функцию – правильная рациональная дробь. Представим в виде суммы простейших дробей. Разложим знаменатель на множители

Тогда

Приведем к общему знаменателю и рассмотрим числители дробей

Воспользуемся комбинированным способом определения коэффициентов. Перепишем предыдущее равенство в виде

Сравнивая коэффициенты при соответствующих степенях и придавая значение , получаем систему:

при , ;

т. е.

Следовательно,

Случай 4. Среди корней знаменателей имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.

Пример 1. Найти интеграл

.

Решение

Так как есть двукратный множитель, то

.

Приведем к общему знаменателю и рассмотрим числители дробей

.

Приравняем коэффициенты при одинаковых степенях x

Следовательно,

.

Заметим, что данный интеграл можно было найти проще с помощью подстановки .

Пример 2. Вычислить интеграл

.

Решение

Выделим целую часть данной неправильной рациональной дроби. Для этого разделим многочлен на многочлен :

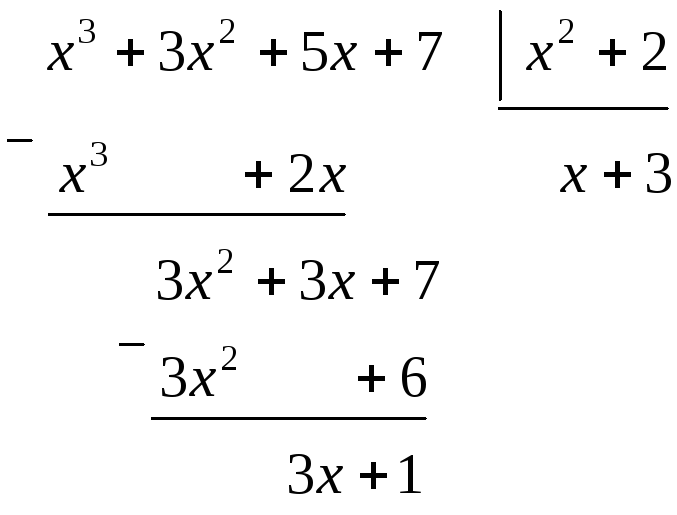
Тогда подынтегральную функцию можно представить в виде суммы целой части и дроби, в числителе которой стоит остаток от деления :

.

Тогда

.