3. Интегралы вида
С
помощью подстановки
этот интеграл приводится к рассмотренному
в п. 1.8.2.
Пример 1. Вычислить интеграл
.
Решение
.
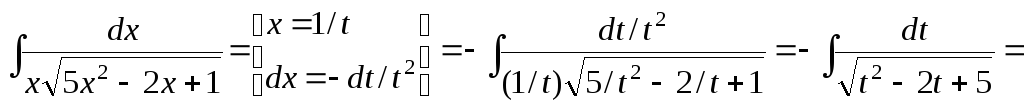
Пример 2. Вычислить интеграл
.
Решение
.
4.
Интегралы дифференциальных биномов
,
где m,
n,
p
– рациональные числа
Интегралы от дифференциальных биномов выражаются через элементарные функции только в трех случаях:
1)
p
– целое число; тогда данный интеграл
сводится к интегралу от рациональной
функции с помощью подстановки
,
где s –
наименьшее общее кратное знаменателей
дробей m
и n;
2)
– целое
число; в этом случае данный интеграл
рационализируется с помощью подстановки
,
где s –
знаменатель дроби p;
3)
– целое число; в этом случае к той же
цели ведет подстановка
,
где s
– знаменатель дроби p.
Пример 1. Вычислить интеграл
.
Решение
Преобразуем подынтегральную функцию
,
т. е.
– целое число. Значит, имеем первый
случай интегрируемости дифференциального
бинома. Поэтому следует применить
подстановку
,
тогда
и искомый интеграл принимает вид
.
Возвращаясь к
исходной переменной по формуле
,
получим
.
Пример 2. Вычислить интеграл
.
Решение
Переписав
подынтегральную функцию в виде
,
имеем
.
Так как
– целое число, то имеет место второй
случай интегрируемости. Используя
подстановку
,
получим
.
Следовательно,
.
Пример 3. Вычислить интеграл
.
Решение
Так
как
,
то
– целое число, т. е. пример соответствует
третьему случаю дифференциального
бинома. Тогда
Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
8.
(ответ:
).
9.
(ответ:
).
1.9. Интегрирование тригонометрических функций
1. Интегралы вида , где r – рациональная функция
Интегралы
указанного вида приводятся к интегралам
от рациональных функций с помощью так
называемой универсальной
тригонометрической подстановки
.
В результате этой подстановки имеем
;
;
.
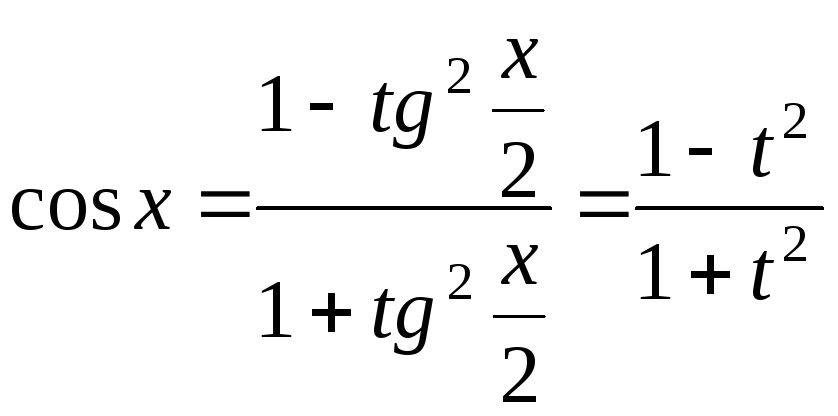Пример 1. Вычислить интеграл
Решение
Воспользуемся универсальной тригонометрической подстановкой и приведенными выше формулами:
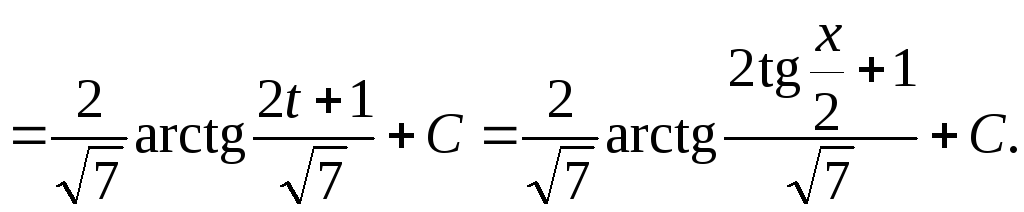
Пример 2. Вычислить интеграл
Решение
Универсальная
тригонометрическая подстановка
во многих случаях приводит к сложным
вычислениям, так как при ее применении
и
выражаются через t
в виде рациональных дробей, содержащих
.
В
некоторых случаях нахождение интегралов
вида
может быть упрощено:
1)
если
– нечетная функция относительно
,
т. е. если
,
то интеграл вычисляется с помощью
подстановки
;
2)
если
– нечетная функция относительно
,
т. е. если
,
то интеграл вычисляется с помощью
подстановки
;
3)
если
– четная функция относительно
и
,
т. е. если
,
то к цели приводит подстановка
.
Пример 3. Вычислить интеграл
Решение
Пример 4. Вычислить интеграл
Решение
Пример 5. Вычислить интеграл
Решение
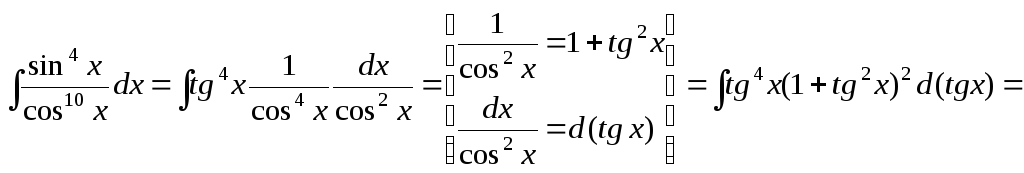
Пример 6. Вычислить интеграл
Решение
2. Интегралы вида
Выделим два случая решения такого интеграла:
1)
если n
– нечетное положительное число, то
применяется подстановка
;
если же m
– нечетное положительное число, то
подстановка
;
2) если оба показателя степени m и n – четные положительные числа, то следует преобразовать подынтегральную функцию с помощью формул
,
,
.
Пример 1. Вычислить интеграл
Решение
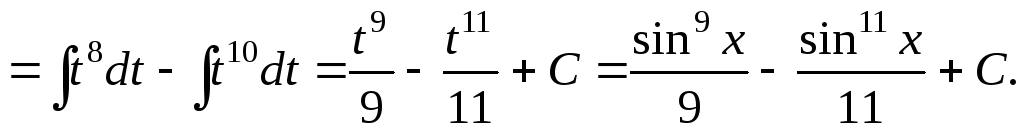
Пример 2. Вычислить интеграл
Решение
Пример 3. Вычислить интеграл
Решение
.
3. Интегралы
вида
и
,
где m
– целое положительное число
При нахождении таких интегралов применяются формулы
или
,
с помощью которых последовательно понижается степень тангенса или котангенса.
Пример 1. Вычислить интеграл
.
Решение
Пример 2. Вычислить интеграл
Решение
Выделим
и распишем по формуле
4. Интегралы
вида
,
,
Тригонометрические формулы
,
,
дают возможность представить произведение тригонометрических функций в виде суммы.
Пример 1. Вычислить интеграл
Решение
Пример 2. Вычислить интеграл
Решение
