1.3. Таблица основных интегралов
Приведём основные формулы для интегрирования элементарных функций. Часть этих формул известна из школьного курса математики.
частный
случай
Приведенные формулы проверяют с помощью дифференцирования. Например, проверим формулу 15:
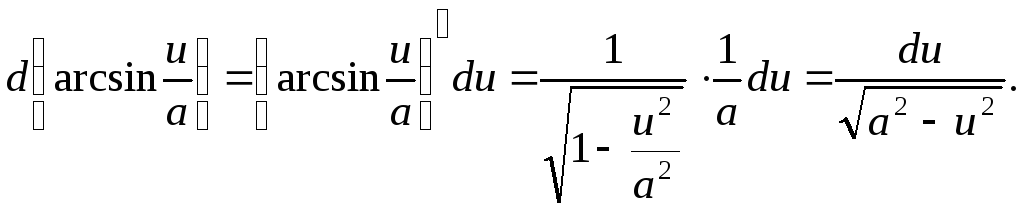
Аналогично убеждаемся в справедливости формулы 3:
.
В качестве упражнения докажите справедливость формул 13, 14, 16.
Примеры. Вычислить интегралы:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
1.4. Замена переменной в неопределенном интеграле. Интегрирование подстановкой
Выполним
в интеграле
формальную замену переменной
интегрирования
(1.6)
Проверим полученную формулу, вычислив производные по x от левой и правой частей равенства:
Таким образом, формула (1.6) доказана. При этом считалось, что
Формула
(1.6) выражает метод
интегрирования подстановкой, или
метод замены
переменной интегрирования. Этот
метод целесообразно использовать в
тех случаях, когда интеграл в правой
части равенства (1.6) проще, чем в левой.
После вычисления нового интеграла
приходится возвращаться к старой
переменной, для чего находят обратную
функцию
Примеры
-
=
. -
. -
.
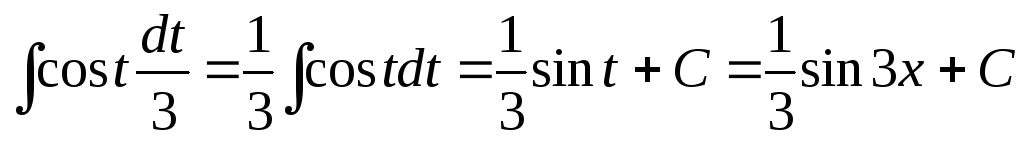4.
.
5.
.
6.
.
7.
.
8.
.
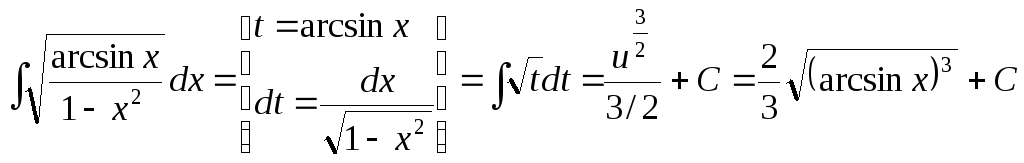Подстановки, использованные в приведенных примерах, весьма просты, и их следует научиться выполнять «в уме», не производя записей с переменной t.
Также для решения можно использовать свойство:
.
9.
.
10.
.
11.
.
12.
.
13.
.
Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
8.
(ответ:
).
9.
(ответ:
).
10.
(ответ:
).
11.
(ответ:
).
12.
(ответ:
).
13.
(ответ:
).
14.
(ответ:
).
1.5. Интегрирование по частям
Второй из основных методов интегрирования базируется на формуле, выражающей дифференциал произведения:
Отсюда имеем
или, рассматривая левую и правую части равенства как подынтегральные выражения, получаем
(1.7)
Произвольная постоянная в правой части равенства не пишется.
Формула
(1.7) выражает метод
интегрирования по частям. Этот
метод уместно использовать в тех случаях,
когда функция u(x)
при
дифференцировании упрощается. Поэтому
в качестве u(x)
выбирают
функции
(по возрастанию сложности).
Пример 1. Вычислить интеграл
Решение
.
Пример 2. Вычислить интеграл
.
Решение
.
Иногда, чтобы свести данный интеграл к табличному, приходится применять формулу интегрирования по частям несколько раз. В некоторых случаях с помощью интегрирования по частям получают уравнение, из которого определяется искомый интеграл (такой интеграл называют циклическим).
Пример 3. Вычислить интеграл
Решение
.
Пример 4. Вычислить интеграл
.
Решение
.
Пример 5. Вычислить интеграл
Решение
.
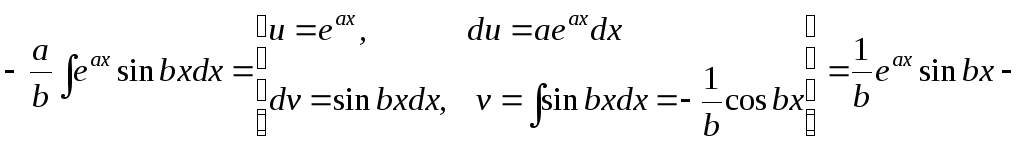
Обозначив исходный интеграл за I, получим уравнение
.
Решим его относительно I:
.
Тогда
.
Пример 6. Вычислить интеграл
.
Решение
.
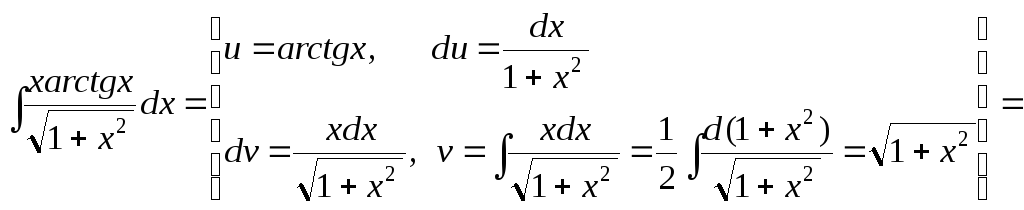
Пример 7. Вычислить интеграл
.
Решение
.
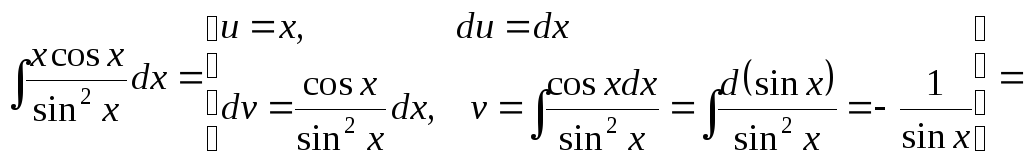
Следует обратить внимание на то, как усложняется вид функции при действии на неё оператора интегрирования. Это явление является типичным.