7.3.2. Вычисление двойного интеграла в полярных координатах

Положение точки М на плоскости можно определить, задав величины:

1. расстояние r от этой точки до начала координат 0;

2. угол между радиусом-вектором и осью Ox (рис. 7.17).

При этом считают, что .

Упорядоченная пара чисел (r, называется полярными координатами точки М. Связь с декартовыми координатами осуществляется при помощи формул

Якобиан

.

Тогда двойной интеграл в полярных координатах

.

Пример 1. Вычислить

Решение

Воспользуемся формулами перехода от декартовых координат к полярным

Так как , то область D – это верхний полукруг радиуса , т. е. изменяется от 0 до . Тогда

Пример 2. Переходя к полярным координатам, вычислить двойной интеграл

, где D – окружность .

Решение

Преобразуем уравнение окружности

.

Это окружность с центром в точке (a; 0) радиуса a (рис. 7.18). Запишем уравнение окружности в полярных координатах

, т.е. .

Причем изменяется в пределах от до , а r – от 0 до . Тогда

=

.

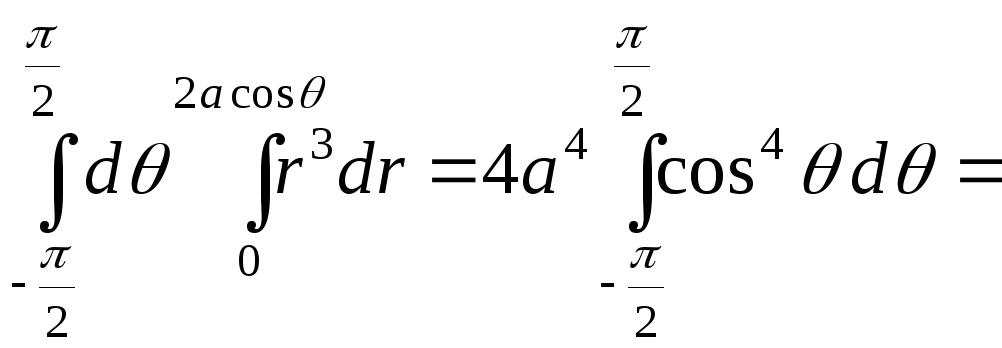
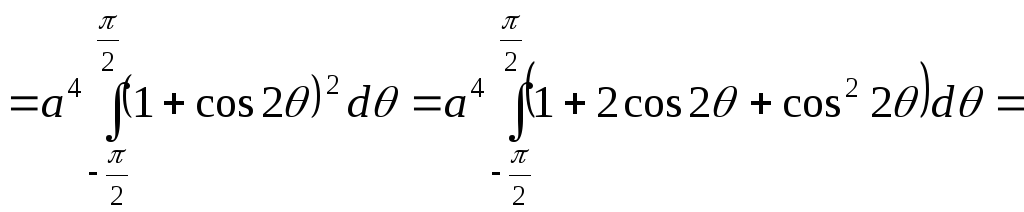
Пример 3. Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования, если

.

Решение

Область D изображена на рис. 7.19. Перейдем к полярным координатам

.

Тогда

.

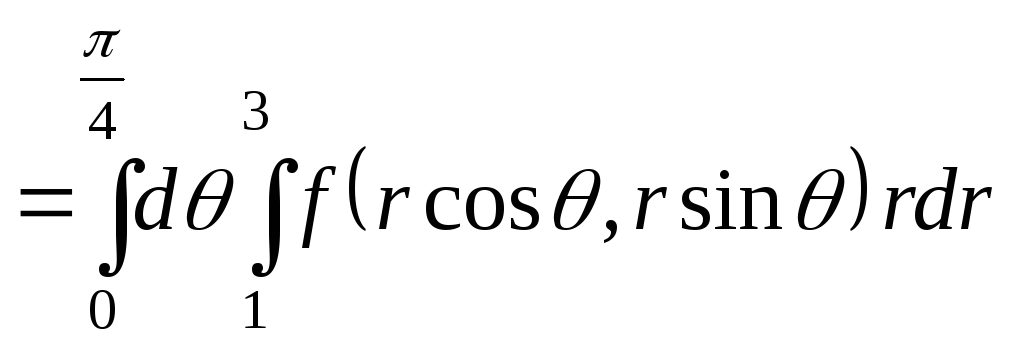Пример 4. Вычислить интеграл

Решение

Для решения перейдем к обобщённым полярным координатам

При этом область S преобразуется в область , коэффициент искажения элемента площади будет равен , где

Поэтому

7.3.3. Вычисление тройного интеграла в цилиндрических координатах

Положение любой точки М в пространстве можно определить, задав три величины:

1. расстояние r от этой точки до оси Oz;

2. угол θ между координатной плоскостью Oxz и плоскостью, проходящей через точку М и ось Oz;

3. расстояние z от точки М до координатной плоскости Oxy (рис. 7.20).

4. П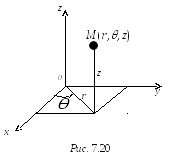ри этом предполагается, что

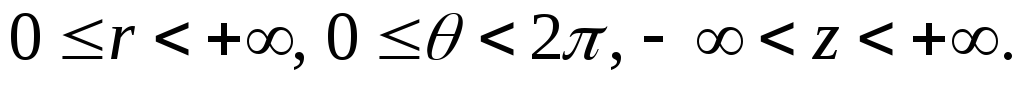
Упорядоченная тройка чисел ( называется цилиндрическими координатами точки М, которые связаны с декартовыми координатами соотношениями:

Цилиндрическая система координат является ортогональной (ортогональны касательные плоскости к координатным поверхностям Координатными поверхностями здесь являются поверхности:

• – цилиндрическая поверхность;

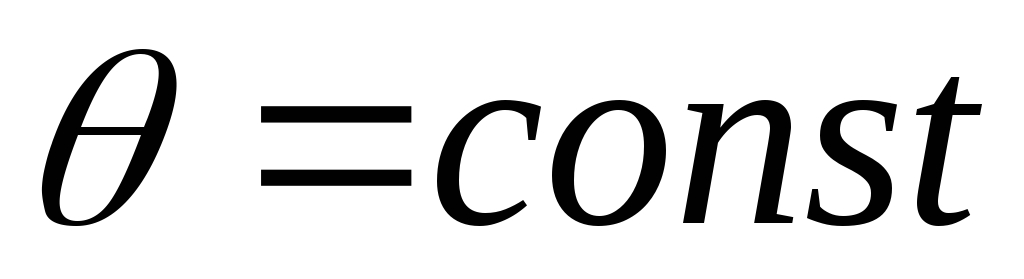• – плоскости, проходящие через ось Oz;

• – плоскости, перпендикулярные оси Oz.

Якобиан отображения в цилиндрическую систему имеет вид

.

Тогда запись тройного интеграла в цилиндрических координатах

Пример 1. Перейти в тройном интеграле к цилиндрическим координатам и расставить пределы интегрирования, если

.

Решение

Область V − это часть цилиндра, ограниченного плоскостями (рис. 7.21). Проекцией на плоскость XOY будет часть окружности, ограниченной прямыми и (рис. 7.22). Уравнение цилиндра в цилиндрических координатах примет вид или . Следовательно, в области V координаты и изменяются так: , , . Поэтому

=.

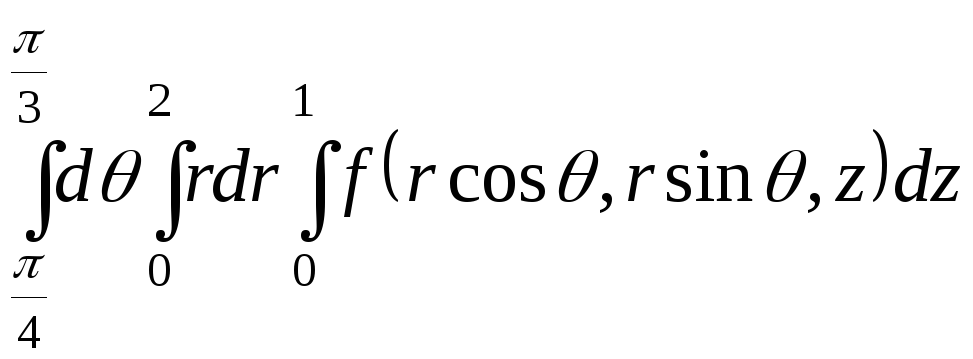Пример 2. Вычислить тройной интеграл

,

где V – область, ограниченная поверхностями и .

Решение

Построим область, ограниченную поверхностями и (рис. 7.23).