3.2. Несобственные интегралы от разрывных функций

Пусть , а в точке x = b она имеет разрыв второго рода. Тогда интеграл

(3.2)

называется несобственным интегралом (сходящимся, если предел (3.2) существует и конечен; расходящимся – в остальных случаях). Несобственные интегралы от разрывных функций называют ещё несобственными интегралами второго рода.

Геометрический смысл несобственного интеграла ясен из рис. 3.3.

Аналогично вводятся несобственные интегралы в случаях, когда подынтегральная функция имеет иначе расположенную точку разрыва. Так, если f(x) имеет разрыв при x = a, т. е. , то

(3.3)

Если точка разрыва x = с лежит между точками x = a и x = b, то

(3.4)

Пример 1. Исследовать сходимость несобственного интеграла

Решение

Поскольку подынтегральная функция имеет разрыв в точке , то, учитывая (3.4), имеем

Очевидно, что интеграл расходится.

Если на отрезке функция f(x) имеет несколько точек разрыва, то несобственный интеграл определяется аналогично.

В некоторых задачах вместо (3.3) целесообразно ввести понятие главного значения несобственного интеграла

(3.5)

Здесь точка разрыва «вырезана» из отрезка вместе с симметричным относительно нее промежутком Поэтому если сходится интеграл (3.4), то сходится и (3.5). Обратное же утверждение неверно: (3.5) может сходиться, а (3.4) – расходиться.

Например, интеграл, рассмотренный в предыдущем упражнении, расходится, хотя существует в смысле главного значения (убедитесь в этом самостоятельно).

Заметим, что в случае, когда функция f(x) имеет разрыв первого рода, нет принципиальной необходимости вводить понятие несобственного интеграла: достаточно разбить отрезок на два отрезка, доопределив на каждом из них f(x) до непрерывности (рис. 3.4) и рассмотрев два обычных интеграла.

Пример 2. Исследовать сходимость несобственного интеграла

.

Решение

Подынтегральная функция терпит бесконечный разрыв в точке

.

Тогда

.

Ответ: Интеграл сходится и его величина составляет .

Пример 3. Исследовать сходимость несобственного интеграла

.

Решение

Подынтегральная функция терпит бесконечный разрыв в точках и . Тогда необходимо представить интеграл в виде суммы двух интегралов

.

Ответ: Интеграл сходится и его величина составляет .

Пример 4. Вычислить несобственный интеграл или установить его расходимость.

Решение

При функция . По формуле (3.3) имеем

Вычислим отдельно первый предел – неопределенность , преобразуем его

.

Тогда

.

Ответ: Интеграл сходится и его величина составляет .

Пример 5. Прямоугольный резервуар с площадью горизонтального сечения наполнен водой до высоты . Определить время, в течение которого вся вода вытечет из резервуара через небольшое отверстие в его дне площадью , если принять, что скорость истечения воды равна , где h – высота уровня воды над отверстием, g – ускорение силы тяжести.

Решение

Высота h уровня жидкости зависит от времени t, т. е. h = h(t). Если жидкость не вязкая и силами поверхностного натяжения можно пренебречь, то скорость v истечения жидкости из сосуда с достаточной точностью описывается законом Торричелли

.

Поэтому объем, вытекший за время dt, равен

.

С другой стороны, тот же объем равен (надо учесть, что h убывает и потому dh < 0). Приравнивая оба выражения, получим, что

, т.е. .

Чтобы получить полное время истечения, надо произвести интегрирование

.

Реально истечение происходит не до h = 0, а до , где – некоторая величина, сравнимая с шероховатостями дна или с толщиной смачивающей пленки, т. е. формулу надо было бы писать в виде

.

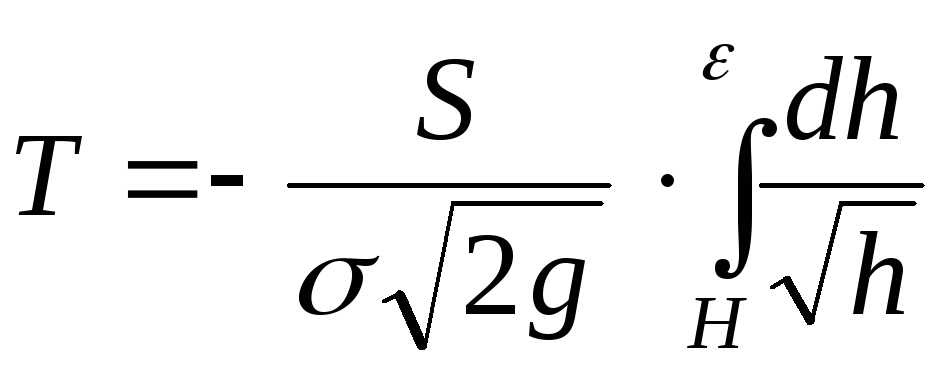Однако несобственный интеграл получился сходящимся (это показали вычисления). К тому же в данном примере нам не было точно известно, но оно и несущественно, так как для сходящегося интеграла важно только знать, что мало. Поэтому, подставляя числовые значения параметров, получим

мин.

Пример 6. Найти потери благосостояния общества при движении к идеальному состоянию, если разность значений целевой функции общественного благосостояния (ЦФБ) при полном удовлетворении потребностей и в момент времени t лет задается функцией .

Решение

Известно, что потери благосостояния общества при движении к идеальному состоянию определяются интегралом

,

где – значение целевой функции общественного благосостояния при полном удовлетворении рациональных потребностей, а – значение ЦФБ в момент времени t.

Определим потери благосостояния общества:

.

Ответ: .

Пример 7. Найти средний срок эксплуатации оборудования, если функция, характеризующая количество оборудования, находящегося в рабочем состоянии по истечении времени t, имеет вид .

Решение

Если l(t) – функция, выражающая количество оборудования, находящегося в рабочем состоянии по истечении времени t лет, то средний срок эксплуатации находится из выражения

.

Определим средний срок эксплуатации оборудования:

.

Первый предел вычисляется с помощью правила Лопиталя

.

Тогда

.

Ответ: .

Пример 8. Определить общую сумму текущих затрат, если функция, характеризующая текущие издержки обращения и капиталовложений, имеет вид .

Решение

Если функция f(t) характеризует изменение издержек обращения и капиталовложений, то общую сумму текущих затрат можно определить по формуле

.

Общая сумма текущих затрат

.

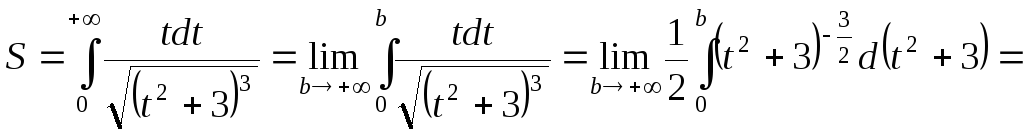
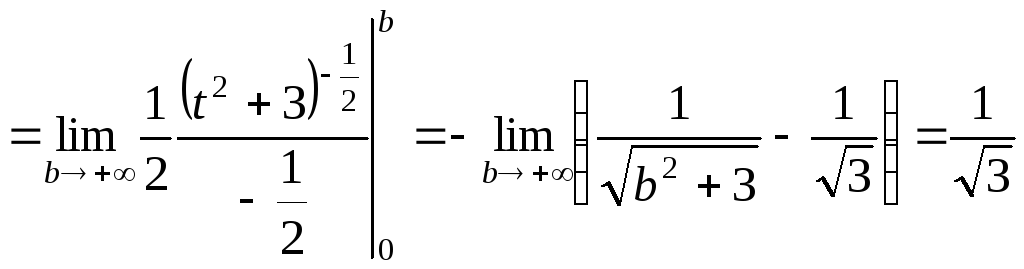Ответ: .