
Весна 16 курс 3 ОрТОР / Теория АД / Термодинамика и теплопередача Никифоров А.И.-2
.pdf
41
Изменение параметров происходит лишь в направлении движения.
Уравнения, полученные при этом условии, строго верны лишь для элементарной струйки, поперечные размеры которой настолько малы, что в каждом ее сечении параметры потока практически постоянны. Следует отметить, что в реальных газовых потоках в пределах поперечного сечения параметры газа могут быть переменными. При использовании уравнений элементарной струйки для таких потоков рассматриваются средние для каждого сечения потока величины (средняя скорость, средняя плотность и т. д.).
Примером движения газового потока при таких допущениях можно считать движение рабочего тела во всех элементах ГТД во время его работы при неизменной частоте вращения, скорости и высоты полета.
7.2. Уравнение неразрывности (расхода)
Это уравнение позволяет рассчитать проточную часть двигателя и связывает параметры и скорость газа (рабочего тела) с площадью поперечного сечения газового потока и определить таким образом габариты ГТД.
Рассмотрим движение газового потока по каналу с непроницаемыми стенками переменного сечения (рис. 7.1), в котором выделим произвольный участок между сечениями 1–1 и 2–2, перпендикулярными скорости потока.
Рис. 7.1. К выводу уравнения неразрывности (расхода)
42
Расход газа G кг/с — количество газа, проходящее через данное поперечное сечение канала (струи) в единицу времени,
G = Fcρ, (7.1)
где F — площадь поперечного сечения канала;
с и ρ — скорость и плотность потока в этом сечении.
Уравнение неразрывности отражает следующую закономерность: при установившемся движении поток газа неразрывен, то есть расход газа,
поступающего в рассматриваемый объем, равен расходу газа, выходящего из этого объема:
G1 = G2.
Следовательно, при установившемся течении газа через любое сечение потока в единицу времени проходит одинаковая масса газа, то есть
G1 = G2 = G = const,
или |
|
|
Fcρ = const. |
(7.2) |
|
Уравнение (7.2) для рассматриваемых сечений 1–1 и 2–2 стационарного |
||
газового потока примет вид |
|
|
F1c1ρ1 = |
F2c2ρ2. |
(7.3) |
Полученные уравнения (7.2) и (7.3) и |
есть уравнения |
неразрывности |
стационарного газового потока, устанавливающие связь между площадью поперечного сечения потока канала F, его скоростью c и плотностью ρ в этом сечении. В этих уравнениях учитывается свойство сжимаемости газа.
В случае движения жидкости или несжимаемого потока газа, для которых
ρ1 = ρ2 = ρ = const, уравнение (7.3) приводится к виду |
|
F1c1 = F2c2. |
(7.5) |
Из уравнения (7.5) следует, что при установившемся течении жидкости и |
|
несжимаемого потока газа скорость потока изменяется обратно пропорционально площади сечения канала.
43
Выполнив логарифмирование и последующее дифференцирование уравнения (7.2), получим уравнение неразрывности в дифференциальной форме:
|
dF |
|
|
dc |
|
d |
0 , |
(7.6) |
||||||
|
F |
|
|
|
||||||||||
|
|
|
c |
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dF |
|
dc |
|
dυ |
|
||||||
|
|
|
|
|
|
|
|
|
. |
(7.7) |
||||
|
|
|
F |
|
c |
υ |
||||||||
Если стенки канала проницаемые и через них может проникать газ, то условие (7.2) не выполняется. В этом случае уравнение неразрывности в дифференциальной форме имеет вид
dF |
|
dc |
|
d |
|
dG |
, |
(7.8) |
|
|
|
|
|||||
F |
c |
|
G |
где dG — изменение расхода газа на элементарной длине канала.
Для произвольного сечения потока, составляющего угол α с направлением нормали к вектору скорости, расход
G F c cos , |
(7.9) |
где Fα — площадь сечения, составляющего угол α с направлением нормали к вектору скорости (рис. 7.1).
7.3. Уравнение первого закона термодинамики
Во второй главе было показано, что уравнение первого закона термодинамики (2.39) определяет баланс между теплом, подведенным к телу
(или отведенным от него), изменением внутренней энергии и работой расширения (сжатия), то есть работой изменения объема. Поэтому уравнение первого закона термодинамики (2.41) применимо и для потока газа:
dQ dU dL СυdT pdυ . |
(7.10) |

44
Уравнение (7.10) является общим, приложимым к любым газовым потокам, в том числе и нестационарным.
Если dυ = 0, то
dQ dU .
Следовательно, если в потоке не совершается работа изменения объема
(pdυ = 0), то все тепло, подведенное (или отведенное) к газу, идет на изменение его внутренней энергии.
Из сказанного следует:
Тепловая форма энергии (внутренняя энергия; энергия, подводимая в виде тепла) в потоке так же, как и в неподвижной среде, может быть преобразована в механическую форму лишь посредством изменения
объема газа.
В том случае, когда рабочее тело несжимаемо (несжимаемая жидкость, dυ = 0), тепло, подводимое к нему, не может быть преобразовано в какой-либо вид энергии механического движения (кинетическая энергия, потенциальная энергия и др.); оно только, как отмечалось, изменит внутреннюю энергию.
Поэтому, например, несжимаемая жидкость не может служить рабочим телом тепловых двигателей.
Для движущегося газа удобно вместо внутренней энергии оперировать понятием «энтальпия». Тогда, воспользовавшись уравнением (2.44), получим другую форму записи уравнения первого закона термодинамики:
dQ Cp dT υdp di υdp . (7.11)
Для того чтобы перейти к интегральной форме уравнения первого закона термодинамики, выделим в потоке газа частицу, которая в начальный момент времени находится в сечении 1–1, и проследим изменение термодинамического состояния этой частицы газа за конечный промежуток времени, в течение которого она переместится в сечение 2–2 (рис. 7.2, а). В процессе движения
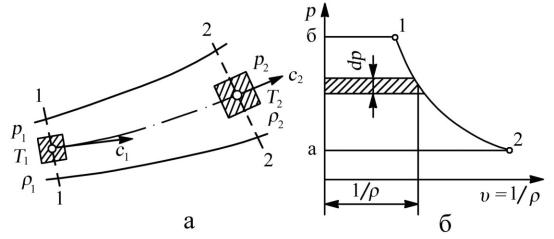
45
выделенной частицы газа происходит ее деформация, то есть она находится в термодинамическом процессе изменения состояния. Это может быть сжатие или расширение. Изобразим его в «p–υ» координатах линией процесса 1–2 (рис.
7.2, б). Интегрируя уравнение (7.11) от начального сечения 1–1 до конечного сечения 2–2 (рис. 7.2, а), считая течение одномерным и относя его величины к
1 кг воздуха, получим уравнение первого закона термодинамики для движущегося газа в интегральной форме
2 |
2 |
dp |
|
|
|
Q i2 i1 υdp i2 |
i1 |
. |
(7.11') |
||
|
|||||
1 |
1 |
|
|
||
В этом уравнении Q — все тепло, которое подводится к газу между сечениями 1–1 и 2–2. Оно состоит из тепла Qвнеш, подводимого к объему газа извне, и того тепла Qr, которое выделяется в результате работы сил трения.
Рис. 7.2. К составлению уравнения первого закона термодинамики для движущегося потока:
а— перемещение элементарной частицы газа от сечения 1–1 до сечения 2–2;
б— изображение процесса расширения движущегося газа в координатах «p–υ»

46
Следовательно,
|
|
|
|
|
2 |
|
|
dp |
|
|
||
|
|
Qвнеш Qr |
i2 |
i1 |
|
. |
(7.12) |
|||||
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|||
В предположении, что тепло трения Qr |
эквивалентно работе сил трения |
|||||||||||
(Qr = Lr), получаем |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
dp |
|
|
|
||
|
|
Qвнеш Lr |
i2 |
i1 |
|
|
. |
(7.13) |
||||
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
||
2 |
dp |
2 |
|
|
|
|
|
|
|
|
|
|
Интеграл |
υdp представляет собой, |
как известно из технической |
||||||||||
|
||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
||
термодинамики (формула 2.38), работу сжатия (расширения) движущегося газа.
Процесс изменения состояния газа в элементах ГТД принято считать политропным и определять указанную работу по выражению
2 |
dp |
|
n |
|
|
|
|
|
|
R(T2 T1 ) LП . |
(7.14) |
||||
|
n 1 |
||||||
1 |
|
|
|
||||
Эта работа численно равна площади aб12 (рис. 7.2, б).
7.4. Уравнение сохранения энергии
Для того чтобы получить уравнение сохранения энергии газового потока,
необходимо выяснить, какими видами энергии обладает движущийся газ, это:
внутренняя энергия U СυT , Дж/кг;
кинетическая энергия U к c2 , Дж/кг;
2
энергия давления (проталкивания) l pυ , Дж/кг.
Энергия давления (энергия проталкивания) имеет смысл для открытой термодинамической системы, то есть для движущегося газа. Она характеризует способность газа перемещаться из области с одним давлением в область с другим давлением.
47
Энергия давления измеряется работой, совершаемой силами давления газа при его движении.
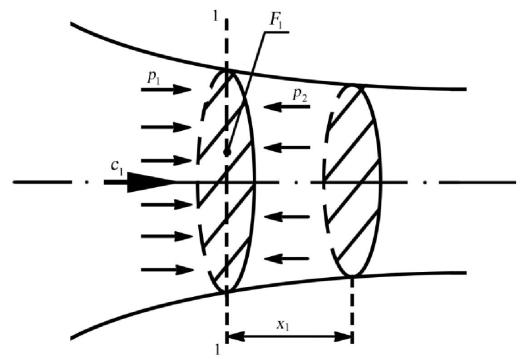
Для того чтобы получить формулу для вычисления энергии давления,
найдем работу сил давления, которая затрачивается на проталкивание 1 кг газа через сечение 1–1 (рис. 7.3).
С обеих сторон рассматриваемого сечения на газ действует сила
P1= p1F1,
где p1 — давление;
F1 — площадь поперечного сечения.
Для перемещения газа из сечения 1–1 на расстояние x1 необходимо преодолеть силу P1, совершив работу по перемещению массы газа
L = P1x1 = p1F1x1,
где произведение F1x1 представляет собой объем 1 кг газа (удельный объем υ),
прошедшего через сечение 1–1, тогда
L = p1υ1.
Рис. 7.3. К выводу формулы энергии давления
48
Величина, равная произведению давления газа на его удельный объем pυ,
представляет собой энергию (работу) проталкивания, или энергию давления.
Таким образом, каждый килограмм движущегося газа обладает кроме собственной внутренней энергии еще и переносимой им энергией проталкивания, которую он получает от внешнего источника.
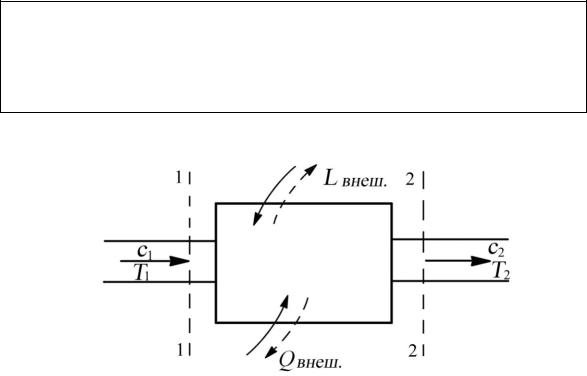
Уравнение сохранения энергии есть частное выражение всеобщего закона сохранения и превращения энергии, записанного применительно к газовому потоку, протекающему через какой-либо из элементов двигателя (рис. 7.4), в
котором в общем случае поток газа может получать или отдавать энергию.
Поскольку при установившемся движении газа его расход через сечения 1–1 на входе и 2–2 на выходе одинаков, все входящие в уравнение сохранения энергии члены принято относить к 1 кг газа. Внешняя энергия может сообщаться
(отводиться) газу как в форме механической работы Lвнеш, так и в форме тепла
Qвнеш.
Согласно закону сохранения энергии полная энергия газового потока на выходе из рассматриваемого элемента 2–2 будет больше (или меньше) полной энергии на входе в него 1–1 на величину сообщенной (отведенной)
энергии между рассматриваемыми сечениями.
Рис. 7.4. К составлению уравнения сохранения энергии

49
Так как полная энергия газового потока в каждом сечении равна сумме внутренней энергии, энергии давления и кинетической энергии согласно сказанному, запишем уравнение сохранения энергии в общем виде:
СυT1 p1υ1 |
c2 |
Lвнеш Qвнеш СυT2 p2υ2 |
c2 |
|
|
1 |
2 |
. (7.15) |
|||
2 |
2 |
||||
|
|
|
Уравнение (7.15) для упрощения расчетов приведем к другому виду,
заменив сумму внутренней энергии и энергии давления энтальпией:
i1 |
c2 |
Lвнеш |
Qвнеш |
i2 |
c2 |
|
||
1 |
2 |
. |
(7.16) |
|||||
2 |
2 |
|||||||
|
|
|
|
|
|
|||
Для энергоизолированного газового потока (Lвнеш = 0, Qвнеш = 0) уравнение сохранения энергии примет вид:
i1 |
c2 |
i2 |
c2 |
const . |
|
|
1 |
2 |
(7.17) |
||||
2 |
2 |
|||||
|
|
|
|
Уравнение (7.17) показывает:
При отсутствии энергообмена полная энергия газового потока в любом сечении элемента двигателя, равная сумме энтальпии и кинетической энергии, сохраняется неизменной.
Важно отметить, что уравнения (7.16) и (7.17) не содержат в явном виде гидравлических потерь, учитываемых в виде работы от сил гидравлических сопротивлений Lr. Они имеют одинаковый вид как при отсутствии, так и при наличии гидравлических потерь. Силы гидравлического сопротивления
(условно называемые также силами трения) возникают из-за наличия трения,
вихреобразования и волнового сопротивления. Для рассматриваемой системы они являются внутренними силами, а работа, затрачиваемая на их преодоление,
переходит практически полностью в тепло (Lr = Qr).
Если же часть этого тепла уходит через стенки наружу, оно должно быть учтено в величине Qвнеш. Поэтому наличие гидравлических потерь приводит

50
только к преобразованию одного вида энергии другой и не отражается на общем балансе энергии. Из уравнения (7.16) следует, что если наличие гидравлических потерь приводит к уменьшению кинетической энергии газа в сечении 2–2, то ровно на столько же в этом сечении увеличивается энтальпия газа. Таким образом, уравнения (7.16) и (7.17) справедливы для установившегося течения вязкого сжимаемого газа. В каждом конкретном случае могут быть различными только направление внешнего воздействия
(подвод или отвод) и вид подводимой или отводимой энергии.
Уравнение (7.16) запишем в другой форме, где слева отражено полное количество энергии, подводимой к газу. Оно складывается из теплоты, подведенной к газу (Qвнеш), и работы внешних сил, подведенной к газу (-Lвнеш), а справа — результат изменения энергии газового потока:
Qвнеш Lвнеш |
i2 i1 |
c2 |
c2 |
|
|
|||
2 |
1 |
, |
(7.18) |
|||||
|
2 |
|||||||
|
|
|
|
|
|
|
||
или, в дифференциальной форме, |
|
|
|
|
|
|
|
|
dQвнеш dLвнеш |
di |
dc2 |
|
. |
|
(7.19) |
||
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
Уравнение сохранения энергии в форме (7.18) можно сформулировать так:
Внешняя энергия, подведенная к потоку газа в виде тепла и работы, идет на изменение энтальпии и кинетической энергии газа.
В случае идеального газа
i2 i1 Сp (T2 T1 ) .
Поэтому для идеального газа уравнение (7.18) можно представить в виде
|
L |
С |
|
(T T ) |
|
c2 |
c2 |
|
||
Q |
|
2 |
1 |
. |
(7.20) |
|||||
p |
|
|
|
|
||||||
внеш |
внеш |
|
2 1 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
||
Или в дифференциальной форме: |
|
|
|
|
|
|
|
|
|
|
dQвнеш dLвнеш |
Сp dT |
dc |
2 |
. |
|
(7.21) |
||||
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
