2.5 Комплексный метод расчета цепей синусоидального тока

В практике расчета цепей синусоидального тока используется комплексный метод, сущность которого заключается в том, что от дифференциальных уравнений, составленных для мгновенных значений, переходят к алгебраическим – для комплексных значений. Осуществляется замена:

а) мгновенного значения тока i – комплексной амплитудой тока ;

б) напряжения на активном сопротивлении –;

в) напряжения на индуктивности –;

г) напряжения на емкости – комплексом.

Например, для электрической схемы (рисунок 2.9) уравнения для мгновенных значений можно записать как:

или

(2.35)

Запишем в комплексной форме:

или

(2.36)

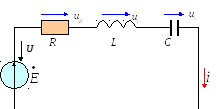
Рисунок 2.9 – Последовательное соединение R, L и С- элементов

Это уравнение позволяет найти комплексную амплитуду тока через комплексную амплитуду ЭДСи сопротивления цепиR, ωL и 1/ωC:

,

(2.37)

где множитель

(2.38)

называют комплексным сопротивлением [Ом], R – действительная (активное сопротивление) и Х – мнимая части (реактивное сопротивление).

Тогда уравнение (2.37) можно записать в виде:

,

(2.39)

что отражает закон Ома для цепи синусоидального тока.

Для схемы рисунка 2.9 реактивное сопротивление равно:

(2.40)

Модуль полного сопротивления равен

(2.41)

Угол сдвига фаз (φ) определяется как

,

(2.42)

а значение угла φ зависит от соотношения:

1. Между реактивным Х и активным R сопротивлениями: чем больше Х, тем больше угол φ.

2. Между индуктивным и емкостным сопротивлениями: а) если , тои ток отстает по фазе от напряжения на угол φ; б) если, тои ток опережает по фазе напряжение на угол φ.

Модуль сопротивления можно представить как гипотенузу прямоугольного треугольника сопротивлений (рисунок 2.10 а).

Рисунок 2.10 – Треугольники сопротивлений (а) и проводимостей (б)

Величина обратная комплексному сопротивлению называется комплексной проводимостью Y:

(2.43)

Действительная часть g и мнимая b. Измеряет проводимость в [Ом^-1=См].

Модуль комплексной проводимости равен (рисунок 2.10 б).

При этом угол φ определяется из треугольников сопротивлений и проводимостей через его тангенс .

Закон Ома при использовании комплексной проводимости:

.

(2.44)

Таким образом, треугольники сопротивлений и проводимостей дают графическую интерпретацию связи между модулем полного сопротивления z и активным R и реактивным Х сопротивлениями цепи или составляющими проводимости g и b.

Применение векторных диаграмм при расчете цепей

Токи и напряжения на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают. Векторная диаграмма токов и напряжений дает наглядное представление о фазовом расположении этих векторов. Построение векторных диаграмм рекомендуется для контроля аналитических расчетов цепей синусоидального тока, который заключается в сравнении направлений векторов на комплексной плоскости, полученных в результате аналитических расчетов с направлениями этих векторов, исходя из физических соображений: U_L опережает I_L, а U_C отстает от I_C.

В качестве примера построим векторную диаграмму цепи рисунка 2.9 для случая, когда (следовательно). При построении векторной диаграммы в качестве начального вектора удобнее выбирать вектор тока, т. к. при последовательном соединении ток по всем элементах протекает один и тот же.Начальный вектор тока совмещаем с положительным направлением вещественной (действительной) оси. Падения напряжения в комплексной форме на участках цепи с активным, индуктивным и емкостным сопротивлениями определяются как:

(2.45)

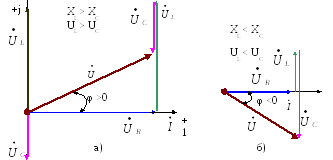
Рисунок 2.11 – Векторные диаграммы режимов электрической цепи

Вектор на участке с активным сопротивлением совпадает по фазе с вектором тока, и на векторной диаграмме его проводим в направлении вектора тока; падение напряженияна участке с индуктивностью опережает ток по фазе на угол(поворачиваем вектор напряжения на этот угол против направления вращения часовой стрелки); падение напряженияна участке с емкостью отстает от тока на угол(поворачиваем вектор напряжения на этот угол по часовой стрелке);

Для нахождения вектора полного напряжения цепи складываем вектора,и(путем параллельного переноса). Вектор полного напряжениясоединяет начало координат с концом последнего слагаемого.

Т. к. мы строили диаграмму для случая, когда , то получаем, что ток в цепи отстает по фазе на уголφ от полного напряжения, комплексное значение которого

.

(2.46)

Аналогично проводят анализ в случае, когда . При этом угол сдвига фаз между током и полным напряжением будет отрицателен (рисунок 2.11 б). Если аналитический расчет дает результаты, не совпадающие с положениями, что на векторной диаграмме напряжение на индуктивностидолжно опережать протекающий через нее ток на; а напряжение на емкости– отставать от тока на, то значит, в решение вкралась ошибка.

Законы Кирхгофа в символической форме записи

По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в узле схемы, равна нулю , а в символической форме. Второй закон Кирхгофа для мгновенных значений:

,

(2.47)

где каждое слагаемое первой части можно заменить на , а второй –.

Тогда второй закон Кирхгофа в символической форме записи:

(2.48)

Так как законы Кирхгофа справедливы и для цепей синусоидального тока, то в случае, когда между электрическими цепями синусоидального тока нет магнитной связи, все расчетные формулы и методы цепей постоянного тока применимы к цепям синусоидального тока. Но в формулах необходимо вместо: постоянного тока I поставить комплекс тока ; проводимостиg – комплексную проводимость Y; сопротивления R – комплексное сопротивление Z; постоянной ЭДС Е – комплексную ЭДС .
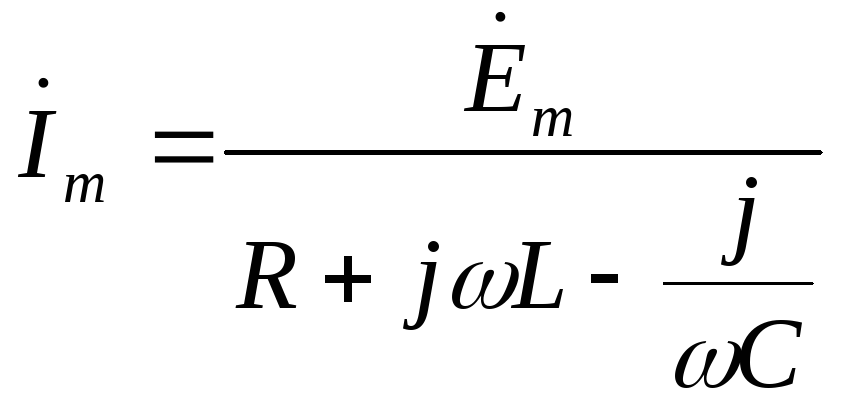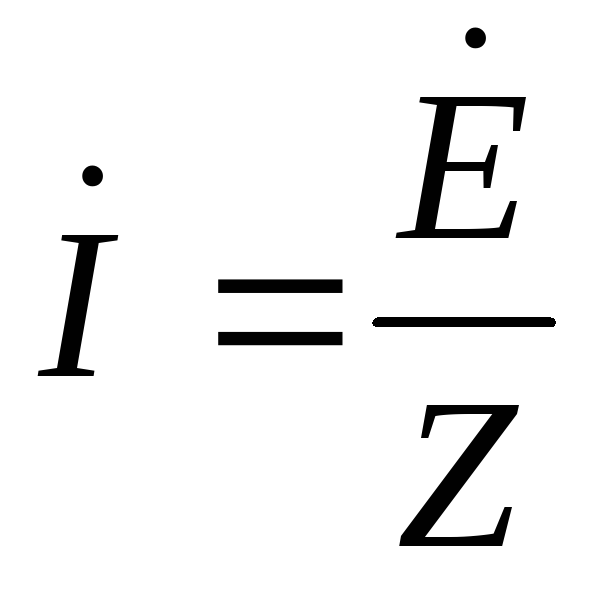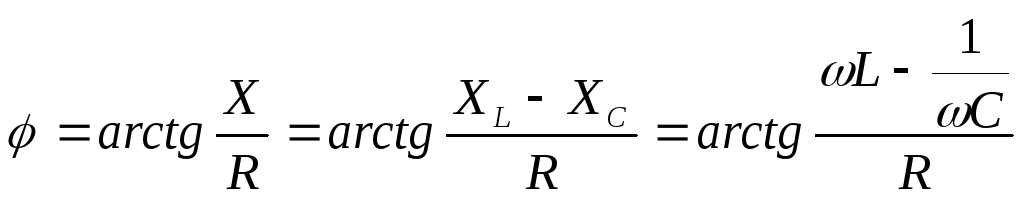