Конспект лекций Высшая математика (Басканова)

430

построению функция (4.3.15) является решением уравнения (4.3.3) в интервале (a, b) при всех значениях произвольной постоянной C. А это и означает, что функция (4.3.15) есть общее решение уравнения (4.3.3) в области (4.3.7).

Пример 1. Рассмотрим уравнение

непрерывная в интервале (−1,+1). Пользуясь формулой (4.3.15), найдем: y = Ce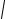1−x2 .

Это есть общее решение рассматриваемого уравнения в области:

−1<x<+1, −∞<y<+∞.

Пример 2. Найти решение уравнения: y′+2xy=0.

В этом случае p(x)=2x не имеет точек разрыва. Поэтому всякое решение определено при всех x. Действительно, интегрируя данное уравнение, получим:

y = Ce−x2 ,

откуда и вытекает наше утверждение.

Решения однородного линейного уравнения обладают следующими двумя характерными для этого уравнения свойствами.

1. Если y1 есть частное решение уравнения (4.3.3), т. е. имеет место тождество

Следовательно, y = Cyl есть решение уравнения (4.3.3).

2. Если y1 – ненулевое частное решение уравнения (4.3.3), то формула (4.3.17), где C – произвольная постоянная, дает общее решение уравнения

(4.3.3) в области (4.3.7).

В самом деле, уравнение (4.3.17) разрешимо в о ластиб ( 4.3.7) относительно C:

и, как показано выше, функция (4.3.17) является решением уравнения (4.3.3) при всех значениях C. Следовательно, функция (4.3.17) есть общее решение уравнения (4.3.3) в области (4.3.7).

Таким образом, для построения общего решения однородного линейного уравнения достаточно найти какое-нибудь одно ненулевое частное решение.

Рассмотрим теперь неоднородное уравнение (4.3.1)

dydx + p(x)y = q(x) .

Предположим, что нам известно некоторое решение y1 этого уравнения, т. е. имеем тождество:

Мы получили для определения z однородное линейное уравнение, левая часть которого имеет тот же вид, что и левая часть уравнения (4.3.3).

Уравнение (4.3.22) называется однородным линейным уравнением, соответствующим неоднородному линейному уравнению (4.3.1). Общее решение уравнения (4.3.22) имеет вид:

Все решения уравнения (4.3.1) содержатся в формуле (4.3.24). Эта формула представляет собою общее решение уравнения (4.3.1) в полосе

a< x <b, −∞<y< +∞ (4.3.25)

т. е. во всей области задания уравнения (4.3.1).

Таким образом, мы приходим к следующей теореме, устанавливающей структуру общего решения линейного неоднородного уравнения.

Теорема. Если y1 есть частное решение неоднородного линейного уравнения (4.3.1),

y′+ p(x)y = q(x)

то общее решение этого уравнения дается формулой (4.3.20), y=y1+z,

432

где

z = Ce−∫ p(x)dx

есть общее решение соответствующего однородного линейного уравнения (4.3.22),

z′ + p(x)z = 0 .

Из этой теоремы следует, что знание одного частного решения неоднородного уравнения (4.3.1) дает возможность получить общее решение при помощи одной квадратуры.

Если мы знаем не одно, а два частных решения y1 и y2 неоднородного уравнения (4.3.1), то общее решение можно получить вовсе без квадратур, а именно общим решением будет

y=y1+C(y2−y1). (4.3.26)

Действительно, из формулы (4.3.20) имеем: z = y − y1; заменяя здесь y на y2, видим, что y2−y1 есть частное решение однородного уравнения (4.3.22).

Тогда общее решение уравнения (4.3.22) дается формулой z = С(y 2−y1) и, согласно доказанной теореме, формула (4.3.26) дает общее решение уравнения (4.3.1).

Выяснив структуру общего решения уравнения (4.3.1), укажем один общий способ фактического построения общего решения

4.3.2. Метод вариации произвольной постоянной (метод Лагранжа)

Будем искать решение уравнения (4.3.1) в том же виде, что и общее решение (4.3.23) соответствующего однородного уравнения (4.3.20), но будем считать C не постоянной, а некоторой непрерывно дифференцируемой функцией от x, т. е. положим

433

Это есть решение уравнения (4.3.1) по построению и притом общее в полосе (4.3.25), так как она имеет структуру (4.3.20).

Таким образом, общее решение неоднородного линейного уравнения (4.3.1) всегда может быть найдено двумя квадратурами.

Замечание. Общее решение неоднородного линейного уравнения (4.3.1) можно найти также следующим методом, принадлежащим Эйлеру.

Умножим обе части уравнения (4.3.1) на функцию

Мы получили тот же вид общего решения, что и при применении метода Лагранжа.

Функция (4.3.30) называется интегрирующим множителем

линейного уравнения (4.3.1), а изложенный метод Эйлера – методом интегрирующего множителя.

Пример 1. Рассмотрим уравнение

y′ − 2x y = x.

Найдем его решение методом вариации произвольной постоянной.

или

434

C′(x) = 1x ,

откуда

C(x) = ln x +C .

Оканчательно получим:

y = x2 (ln x + C).

Это и есть общее решение уравнение.

Проинтегрируем это уравнение методом интегрирующего множителя. Имеем:

Пример 2. Найти общее решение уравнения xy′+2x2y=1, пользуясь формулой общего решения (4.3.29).

Имеем:

p(x)=2x, q(x)=1/x.

Подставляя в формулу (4.3.29) получим:

4.3.3. Уравнение Бернулли

Определение 3. Уравнение вида

y′+p(x) y = q(x)ym (4.3.35)

где m − любое вещественное число, называется уравнением Бернулли. Будем считать, что m отлично от0 и 1,ибо в этих случаях уравнение Бернулли вырождается в линейное. Относительно функций p(x) и q(x) будем

предполагать, что они непрерывны в интервале (a, b).

Уравнение Бернулли всегда может быть сведено к линейному

435

уравнению. В самом деле, преобразуем сначала правую часть уравнения Бернулли к виду правой части линейного уравнения. Для этого разделим обе части уравнения (4.3.35) на ym:

Деля уравнение (4.3.35) на ym, теряем решение y = 0. Очевидно, что это могло случиться лишь при m > 0. Поэтому решение y = 0 также является решением уравнения (4.3.35), которое не содержится в формуле общего решения (4.3.40).

В качестве простейших примеров, иллюстрирующих сказанное, могут служить уравнения y′ = y2 и y′ = 2y . Для первого из них решение y=0 –

частное, для второго – особое.

Пример. Найти решение уравнения

y′ − 1x y = − 1x y2 .

Это – уравнение Бернулли. Деля обе части на y2, имеем: y−2 y′ − 1x y−1 = − 1x .

Полагая

y−1=z,

получим:

z′ + 1x z = 1x

Интегрируя это (линейное) уравнение, находим: z = 1x (C + x).

Следовательно,

436

y = x +x C .

Решениями будут также полуоси оси Ox: y=0 (x≠0).

437

ЛЕКЦИЯ 4.4. УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.

Относительно функций M и N мы будем предполагать, что они непрерывны по обеим переменным в некоторой односвязной области и ни в

При этом функция U является интегралом уравнения (4.4.1). Особых решений уравнение в полных дифференциалах, очевидно, не имеет.

Поэтому возникают два вопроса: 1) как узнать по виду уравнения (4.4.1), является ли оно уравнением в полных дифференциалах? 2) В случае положительного ответа на первый вопрос, как построить функцию U и, следовательно, общий интеграл уравнения (4.4.1)?

Предположим, что функции M(x,y) и N(x,y) имеют непрерывные частные производные соответственно по y и по x. Пусть левая часть уравнения (4.4.1) представляет собою полный дифференциал, т. е.

Дифференцируя первое из этих тождеств по y, а второе по x, получаем тождества:

левые части полученных тождеств равны между собою, а тогда равны и правые, т. е.