Конспект лекций Высшая математика (Басканова)

359

Точное значение объема получают в пределе, который дает линейный интеграл от функции S(x) на интервале [α,b]

Таким образом, объем тела произвольной формы можно найти с помощью линейного интеграла, если известен закон изменения площади его поперечного сечения, т.е. известна функция S(x).

3.9.4. Вычисление двойного интеграла путем сведения к линейному

Требуется вычислить двойной интеграл от функции z = f(x,y) по правильной плоской области D :

f (x, y)ds (3.9.1)

D

Область D называют правильной, если прямые, параллельные координатным осям, пересекают ее границу не более чем в двух точках (Рис. 3.9.2а). Неправильную область можно разбить на части и представить как объединение правильных областей, например D1 и D2 (Рис.3.9.2б).

Плоскую область D правильной формы считают заданной, если из-

вестны уравнения ограничивающих ее линий.

Напомним, что элементарные части (элементарные области), на которые разбивают область D при составлении интегральной суммы, были обозначены в круглых скобках:

( S1),( S2 ),...,( Si ),...,( Sn ),

а их меры (площади) тем же символом без круглых скобок:

S1, S2 ,..., Si ,..., Sn .

Найдем удобное выражение для меры элемента области – ds.

Для этого разобьем D на элементарные части прямыми, параллельными координатным осям (Рис.3.9.2а). Тогда мера элементарной части будет равна площади прямоугольника:

360

ds dxdy

идвойной интеграл (3.9.1) можно записать так:

f (x, y)dxdy (3.9.2)

D

Известно, что двойному интегралу дают геометрическую интерпретацию: он равен объему цилиндрического тела, основанием которого является область D, а сверху это тело ограничено графиком подынтегральной функции z = f(x,y) (Рис. 3.9.3). Следовательно, задачу о вычислении двойного интеграла можно свести к задаче вычисления объема тела с известным поперечным сечением. Найдем объем цилиндрического тела, изображенного на рисунке 3.9.3, по формуле:

b

V S(x)dx (3.9.3)

Для этого, спроектируем крайние точки А и В основания цилиндра (области D) на ось Ох, в результате получим отрезок [α,b], в пределах которого изменяется переменная х. При этом точки А и В делят границу области D на две линии. Пусть уравнения этих линий соответственно равны: y1(x); y2(x), тогда переменная y внутри D будет изменятся от своих значений на линии y1(x) до значений на y2(x).

Рассечем тело плоскостью х = х0, перпендикулярной оси Ох. В сечении получим криволинейную трапецию, ограниченную сверху линией пересечения графика подынтегральной функции z = f(x,y) и плоскости х = х0. Уравнением этой линии является функция одного аргумента

z = f(x0,y)

где х0 = const, y – независимая переменная.

Площадь полученной криволинейной трапеции равна линейному интегралу:

362

область. Затем находят проекции (α,b) крайних точек области на эту ось и по чертежу определяют переменные пределы для внутреннего интеграла.

Пример 1. Вычислить двойной интеграл от функции f(x,y) = x – y по области D, ограниченной линиями: y = x2, y = x.

Решение. Спроектируем построенную область на ось Oх (Рис. 3.9.4). Точки пересечения графиков функций y = x2 и y = x – есть крайние точки области.

Найдем их проекции:

x2 = x; x1 = 0; x2 = 1

Таким образом, внутри области D переменная x изменяется от 0 до 1. Пределы изменения второй переменной y будут зависеть от x. Чтобы найти их, проведем прямые параллельные оси Оy, пересекающие область D. Эти прямые для различных значений

x входят в область на линии y = x2 и выходят из области на линии y = x (Рис.3.9.4). Следовательно, переменная y внутри области изменяется от значений на линии y = x2 до значений на линии y = x.

Подставляя вместо y верхний и нижний пределы, получим:

Как отмечалось выше, чтобы внешний интеграл вычислялся по переменной y, нужно область D спроектировать на ось Oy. Найдем проекции крайних точек области на эту ось:

y y; y1 0; y2 1 (Рис. 3.9.4).

Тогда значения переменной x в области D будут изменятся от ее значений на уравнении прямой x = y до ее значений на уравнении параболы, ре-

363

В обоих случаях результат вычислений один и тот же.

Когда область D является прямоугольником со сторонами, параллельными координатным осям (Рис.3.9.5), пределы становятся постоянными не только внешнего, но и внутреннего интегралов. В этом случае формулы приведения двойного интеграла к двукратному интегрированию становятся очень простыми:

f (x, y)dxdy dx f (x, y)dy dy f (x, y)dx

т.е. порядок интегрирования можно брать любой.

3.9.5. Сведение тройного интеграла к трехкратному интегрирова-

нию

Нужно найти значение тройного интеграла от функции трех переменных u = f(x,y,z) по пространственной области W с объемом V:

f (x, y, z)dv (3.9.6)

W

где dv – мера элемента области (элементарный объем).

Будем считать, что пространственная область (тело) W ограничена одной замкнутой поверхностью, уравнение которой известно

z = z(x,y)

Как и в случае двойного интеграла найдем удобное выражение для меры элемента тела – dv. Для этого разобьем область W на элементарные части плоскостями, параллельными координатным

плоскостям (Рис. 3.9.6).

Тогда за dv можно принять объем параллелепипеда dv = dxdydz и тройной интеграл примет вид:

f (x, y, z)dxdydz (3.9.7)

W

365

В формуле (3.9.8) внутренний интеграл берут по переменной z, при этом x и y считают постоянными. После его вычисления и подстановки пределов остаются две переменные x и y. Следующий интеграл вычисляют по переменной y – при условии, что х = const. После его вычисления остается одна переменная x, по которой берут последний внешний интеграл. Пределы внешнего интеграла постоянны. Рассмотрим несколько примеров связанных с вычислением тройных интегралов.

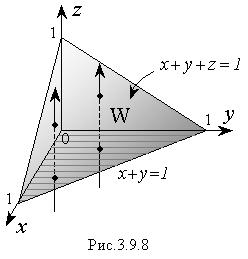
W ограничена координатными плоскостями: х = 0; y = 0; z = 0, и плоскостью x + y + z = 1.

Решение. Область W представляет собой тетраэдр, ограниченный сверху плоскость x + y + z = 1, которая пересекается с осями координат в точках х = 1; y = 1; z = 1 (Рис.3.9.8). Чтобы найти пределы изменения переменной z в области W, проведем пересекающие тетраэдр прямые, параллельные оси Oz. Эти прямые будут входить в тетраэдр на координатной плоскости z = 0, а выходить из него на плоскости x + y + z = 1.

Следовательно, значения переменной z внутри области W будут изменяться от 0 до z = 1 – x – y. Таким образом, верхний предел для z непостоянен и зависит от (x,y), т.е. от координат точки на плоскости xОy, через которую проходит пересекающая тетраэдр прямая (Рис 3.9.8). Проекцией области W на плоскость xOy является треугольник, ограниченный осями координат Ox, Oy и прямой x + y = 1 (Рис.3.9.8). Если его спроектировать на ось Ox, то переменная x внутри треугольника будет изменятся от 0 до 1, а переменная y – от 0 до ее значений на прямой x + y = 1; y = 1 – x. В результате тройной интеграл сводится к трехкратному линейному вида:

Вычислим сначала внутренний интеграл по переменной z, считая x и y постоянными

367

ЛЕКЦИЯ 3.10. ЗАМЕНА ПЕРЕМЕННЫХ В КРАТНЫХ ИНТЕГРАЛАХ. ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ. ТРОЙНОЙ ИНТЕГРАЛ В ЦИЛИНДРИЧЕСКИХ И СФЕРИЧЕСКИХ КООРДИНАТАХ

В силу того, что вычисление двойных и тройных интегралов сводят к двукратному и трехкратному интегрированию, эти интегралы получили название кратных.

Замена переменных в кратных интегралах, так же как в линейном интеграле, часто существенно упрощает их вычисление.

3.10.1. Общий случай замены переменных в двойном интеграле

Рассмотрим двойной интеграл f (x, y)dxdy, где dxdy = ds мера элемен-

D

та плоской области D в декартовой системе координат, f(x,y) – интегрируемая функция, заданная на точках области D.

Пусть с помощью функций:

x x(u, ) (3.10.1) y y(u, )

осуществляют переход от старых координат x, y к новым u, υ.

Эти функции должны быть непрерывными вместе со своими частными производными и однозначно решаться относительно u и υ. При этих условиях каждой точке М на плоскости xOy соответствует единственная точка М* в криволинейной системе координат u и υ, и область D будет однозначно отображаться в область D* (Рис. 3.10.1).

При переходе от декартовых к криволинейным координатам элемент площади dxdy преобразуется в элемент площади dudυ при этом они связаны соотношением:

368

dxdy J dud (3.10.2)

где J – функциональный определитель Якоби, или Якобиан, он равен:

u

Таким образом, замену переменных интегрирования в двойном интеграле осуществляют по формуле:

f (x, y)dxdy f x(u, ), y(u, ) J dud (3.10.3)

D D*

Из выражения (3.10.3) следует, что для того чтобы в двойном интеграле перейти к новым переменным интегрирования, нужно: переменные x и y заменить функциями (3.10.1), вместо элемента площади ds = dxdy подставить выражение J dudυ и область D заменить ее отображением D*. Затем, вычис-

ление двойного интеграла (3.10.3) сводят к последовательному вычислению двух линейных интегралов по новым переменным u и υ.

3.10.2. Двойной интеграл в полярных координатах

Перейдем в двойном интеграле от декартовых к полярным координатам по формуле (3.9.3), при этом за u примем полярный радиус r, а за υ – угол φ:

f (x, y)dxdy f x(r, ), y(r, ) J drd

и двойной интеграл в полярной системе координат примет вид:

f (x, y)dxdy f r cos ,r sin rdrd (3.10.5)

D D*