
Конспект лекций Высшая математика (Басканова)
.pdf
249
2)Проверить принадлежат ли критические точки отрезку a;b .
3)Найти значения функции в критических точках, принадлежащих интервалу a;b и на концах отрезка a;b .
4)Среди найденных значений выбрать наибольшее (наименьшее) зна-
чение.
|
|
|
|
Пример. |
|
|
Найти |
|
|
наибольшее |
и наименьшее |
|
значения |
функции |
|||||||||||||||||||||||||||
f |
x |
|
3 |
x |
|
x |
|
2 |
|
на отрезке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Решение: |
|
|
|
|
f |
|
x |
|
|
непрерывна на отрезке |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1) Функция |
|
|
|
|
|
|
1;1 . |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
2 2x 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
f |
x 3 3 x2 x 2 |
|
x |
3 3 x2 , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
f x 0 при x1 |
|
1 , |
f x – не существует при x2 |
0 . |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2) x , x |
|
|
|
1;1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3) |
|
y |
f |
|
|
1 |
|
|
3 |
|
|
, |
y |
|
f 0 0 . |
На |
|
концах |
отрезка: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
2 |
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y3 f 1 3 , y4 f 1 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
4) |
y3 |
является наибольшим значением функции, а y1 – наименьшим. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
Ответ: |
f |
|
|
|
|
y |
|
f |
1 3 , |
|
f |
|
|
y |
f |
1 |
|
|
3 |
. |
|
||||||||||||||||
|
|
|
|
max |
|
|
min |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
2 3 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач математики, физики, химии и других дисциплин.
Пример. Сечение горной выработки, закрепленной штанговой крепью, на прямолинейном участке обычно имеет прямоугольную форму (например,
просек или печь). Площадь поперечного сечения выработки S 5,12м2 . Оп-
ределить наименьший периметр крепежной рамы, если её длина не превышает 4м.
Решение: Пусть длина рамы a x м, по условию задачи 0 x 4. Так как рама прямоугольной формы, то S a h , где a – длина, h – высота. Тогда h Sa или h 5,12x . Выразим периметр рамы P , как функцию от x :
P a 2h P x x 10,24x .
Фактически, найти наименьший периметр рамы, означает найти наименьшее значение функции P x на интервале 0;4 .
|
|
|
|
250 |
|
|
|
|
P x 1 |
10,24 , |
P x |
0 1 |
10,24 |
0; |
10,24 1; |
x 2 10,24; |
x1,2 3,2 . |
|
x2 |
|
|
x2 |
|
x2 |
|
|
x1 3,2 |
0;4 , |
x2 3,2 0;4 . |
|
|
|
|
|
|
Найдем значение функции P x в критической точке x2 |
и на границе |
|||||||
интервала: P 3,2 |
3,2 |
10,24 6,4 , |
P 4 4 10,24 6,56 . |
|
||||
|
|
|
3,2 |
|
|
4 |
|
|
Следовательно, наименьшее значение функции – P 6,4 достигается в точке x 3,2 .
Ответ: Наименьший периметр крепежной рамы, длина которой не
превышает 4м, а площадь поперечного сечения выработки равна 5,12м2 , равен 6,4м.
251
ЛЕКЦИЯ 2.15. ЭКСТРЕМУМЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2.15.1 Локальные экстремумы функции двух переменных
|
|
Определение. Точка M0 x0; y0 назы- |
||||
|
z |
вается точкой |
экстремума |
(максимума |
||
|
f(x0;y0) |
или минимума) |
функции z f x, y , опре- |
|||
|
|
|||||
|
|
деленной в некоторой области |
D , если су- |
|||
|
|
ществует |
такая |
|
– окрестность точки |
|
|
|
M0 x0; y0 , что для каждой точки M x; y , |
||||
|
y |
отличной от M0 x0; y0 , из этой окрестно- |
||||
|
D |
сти |
выполняется |
неравенство |
||
|
P0(x0;y0) |
f x, y f x0; y0 f x, y f x0; y0 (см. |
||||
|
|
|||||
x |
рис. 2.15.1 |
рис. 2.15.1, 2.15.2). |
При этом значение |
|||
|
f x0; y0 |
называется экстремальным зна- |
||||
|
|
|||||
чением функции (соответственно максимальным или минимальным).
В силу определения, точка экстремума
zфункции лежит внутри области определения функции; максимум и минимум имеют локаль-
|
|
|
ный характер. В области |
D функция |
может |
||||
|
|
|
иметь несколько экстремумов или не иметь ни |
||||||
|
f(x0;y0) |
одного. |
|
|
|
|
|
||
|
|
|
y |
Рассмотрим |
условия |
существования экс- |
|||
D |
P0(x0;y0) |
тремума функции z f x, y . |
|
||||||
|
|
||||||||
x |
|
|
|
Теорема 1. (Необходимые условия экс- |
|||||
рис. 2.15.2 |
|
||||||||
|
|
|
тремума) |
|
|
|
|
|
|
Если в точке M0 x0; y0 |
дифференцируемая функция z f x, y |
имеет |
|||||||
экстремум, то |
её |
частные |
производные |
в |
этой |
точке равны |
нулю: |
||
fx x0; y0 0 , |
fy x0; y0 0 . |
|
|
|
|
|
|
||
Доказательство: |
Зафиксируем |
одну |
из |
переменных. |
Пусть |
||||
y y0 z f x; y |
f |
x, y0 x – |
функция одной переменной, которая |
||||||
имеет экстремум при |
x x0 . |
Следовательно, согласно необходимому усло- |
|||||||
вию экстремума функции одной переменной |
(см. |
теорема 2 п.2.14.2), |
|||||||
x0 0 , т.е. |
fx x0; y0 0 . |
Ч. и т. д. |
|
|
|
|
|||
Аналогично доказывается, что fy x0; y0 0 .

252 |
|
Геометрически равенства fx x0; y0 0 и |
fy x0; y0 0 означают, что в |
точке экстремума функции z f x; y касательная плоскость к поверхности,
изображающей |
функцию |
f |
x; y , параллельна плоскости |
XOY , |
так как |
||||
уравнение касательной плоскости есть z z0 (см. рис. 2.7.5 п.2.7.2). |
|
|
|||||||
|
Функция может иметь экстремум в точках, где хотя бы одна из частных |
||||||||
производных не существует. |
|
|
|
|
|
|
|||
|
z |
|
|
Пример. |
z 1 |
x2 y2 |
имеет макси- |
||
|
|
|
|
мум в точке O 0;0 |
(см. рис. 2.15.3), но не |
||||
|
|
|
|
имеет в этой точке частных производных. |
|||||
|
1 |
|
|
Определение. Точки, в которых част- |
|||||
|
|
|
|
ные производные первого порядка функции |
|||||
|
-1 |
|
|
z f x; y равны нулю, т.е. |
fx 0, |
fy 0 , |
|||
-1 |
0 |
1 |
y |
называются |
стационарными |
точками |
|||
|
1 |
|
|
функции z f x; y . |
|
|
|
|
|
|
|
|
Определение. Стационарные |
точки и |
|||||
x |
рис. 2.15.3 |
|
|||||||
|
|
точки, в которых хотя бы одна частная про- |
|||||||
|
|
|
|
||||||
изводная не существует, называются крити-
ческими точками.
В критических точках функция может иметь экстремум, а может не иметь.
Утверждение, обратное теореме 1 не всегда верно.
Пример. Функция z xy . Для неё точка O 0;0 является критической, так как zx y и zy x обращаются в ноль. Но экстремума в ней функция z xy не имеет, так как в достаточно малой окрестности точки O 0;0 най-
дутся точки, для которых z 0 (I и III четверти) и z 0 (точки II и IV четвертей).
Теорема 2. (Достаточное условие экстремума)
Пусть в стационарной точке M0 x0; y0 и некоторой её окрестности функция f x; y имеет непрерывные частные производные до второго по-
рядка включительно. |
|
|
M0 x0; y0 значения |
|
; y0 |
, |
|
; y0 |
, |
|||
Вычислим в точке |
||||||||||||
A fxx x0 |
B fxy x0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
С fyy x0; y0 . |
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим |
|
A |
B |
|
A C B2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
B |
C |
|
|
|
|
|
|
|
|
|
Тогда:
|
253 |
|
– если 0 , то функция |
z f x; y |
в точке M0 x0; y0 имеет экстре- |
мум: максимум, если A 0 ; минимум, если |
A 0; |
|
–если 0 , то функция z f x; y в точке M0 x0; y0 не имеет экстремума;
–если 0 , то экстремум может быть, а может и не быть. Т.е. требуются дополнительные исследования.
Теорему 2 примем без доказательства.
Используя теоремы 1,2, рассмотрим алгоритм исследования функции
двух переменных на экстремум.
1) Найти область определения функции.
2) Найти стационарные точки, решая систему уравнений zx 0,
zy 0.
3)Убедиться в том, что полученные точки принадлежат области определения функции, если это не так, то точка не является точкой экстремума.
4)Найти частные производные второго порядка заданной функции.
5)Для каждой стационарной точки найти и сделать вывод
Пример. Найти экстремум функции z x3 |
8y3 6xy 1. |
|
|||||||||||||||||||||||
Решение: Область определения функции вся плоскость XOY . |
|
||||||||||||||||||||||||
zx 3x2 |
6y , zy 24 y2 6x . Точки, в которых частные производные не су- |
||||||||||||||||||||||||
ществуют, отсутствуют. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдем стационарные точки, решая систему уравнений. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
0, |
|
|
2 |
6 y 0, |
y |
2 |
x |
|
, |
|
|
|||||||||
|
|
zx |
|
3x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 2 |
|
|||||
|
|
zy |
|
24 y2 |
6x 0. |
24 |
|
x |
6x 0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6x4 6x 0 , 6x x3 1 0 , x1 0 и x2 1. |
|
|
|
||||||||||||||||||||||
Тогда y |
1 |
0 |
2 |
0 и |
y |
|
|
1 |
2 |
|
1 |
. |
Получили две точки возможного |
||||||||||||
|
|
2 |
|
1 |
|
|
|||||||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
экстремума M1 0;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
и M2 1; |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь найдем вторые частные производные данной функции: zxx 6x , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zxy 6 |
, zyy 48y . |
|
M1 0;0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В |
точке |
|
|
|
|
|
|
имеем: |
|
|
|
A 0, |
B 6, C 0 , |
отсюда |
|||||||||||
A C B2 0 6 2 36 0 . Таким образом, в точке M1 0;0 функция экстремума не имеет.

255
2)Найти наибольшее и наименьшее значения функции на границах об-
ласти.
3)Сравнить все найденные значения и сделать вывод.
Пример. Найти |
наибольшее |
и |
наименьшее |
значения функции |
||||||
z x2 y2 xy x y |
в замкнутой области, ограниченной линиями: |
x 0 , |
||||||||
y 0 , |
x y 3 . |
|
|
|
|
|
|
|
|
|
y |
|
|
|
Решение: Данная область треугольник (см. |
||||||
|
|
|
|
рис. 2.15.4). |
|
|
|
|
|
|
3 |
B(0;3) |
|
1) Найдем стационарные точки: |
|
||||||
|
z 2x y 1 0, |
|
y 2x 1, |
|
||||||
|
|
|
|
x |
|
|
2 2x 1 x 1 0. |
|
||
|
D |
|
|
zy 2 y x 1 0. |
|
|||||
O(0;0) |
A(3;0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
3 |
x |
4x 2 x 1 0, 3x 3, x 1 y 2 1 1 1. |
|||||||
|
|
|
|
Следовательно, функция имеет единствен- |
||||||
|
|
рис. 2.15.4 |
D . |
ную стационарную точку M1 |
1;1 , которая при- |
|||||
надлежит |
области |
Найдем |
значение |
функции |
в этой |
точке: |
||||
z 1;1 1 1 1 1 1 1, т. е. z 1;1 1. |
|
|
|
|
|
|||||
2) Исследуем функцию z f x; y |
на границе области, состоящей из |
|||||||||
участков: AB, BO,OA (см. рис. 2.15.4). |
|
|
|
|
|
|||||
– на участке AB : x y 3 y 3 x
zx2 3 x 2 x 3 x x 3 x
x2 9 6x x2 3x x2 x 3 x 3x2 9x 6, zx 6x 9 0 x 32 y 3 x 3 32 32 ,
т. е. имеем |
точку |
|
|
|
|
|
3 |
; |
3 |
|
D . |
Значение |
функции в |
этой точке: |
|||||||||||||||||||||||||
|
|
|
M2 |
2 |
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
; |
3 |
3 |
2 |
|
|
|
3 |
6 |
|
27 |
|
27 |
6 |
3 |
, т. е. z |
3 |
; |
3 |
|
|
3 |
||||||||||||||||
z |
2 |
3 |
|
|
9 |
2 |
4 |
2 |
|
4 |
|
|
2 |
|
|
; |
|||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|||||||||||
|
|
|
– на участке BO : x 0 z y2 |
y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
zy |
2 y 1 0 y |
1 |
|
, т. е. |
|
имеем точку |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
M3 0; |
2 |
D . Значение функции в |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
этой точке: |
|
|
1 |
|
|
|
1 2 |
|
|
1 |
|
|
1 |
|
1 |
|
1 |
, т.е. |
|
|
0; |
1 |
|
|
1 |
; |
|
|
|||||||||||
z 0; |
2 |
|
|
|
|
|
2 |
|
4 |
2 |
4 |
z |
2 |
|
4 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
256 |
|
|
|
|
|
|
|
|
|
– на участке OA : |
y 0 z x2 x , |
zx 2x |
1 0 x 1 , т. е. имеем |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
точку |
|
|
;0 |
|
|
|
|
Значение |
|
|
функции |
в |
этой |
точке: |
||||||||
|
|
M4 |
2 |
D . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
;0 |
|
|
1 2 |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
1 |
; |
|
|
|
|
z |
2 |
|
|
|
2 |
4 |
, т.е. z |
;0 |
4 |
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
– рассмотрим граничные точки области: A 3;0 , B 0;3 ,C 0;0 . |
|
|||||||||||||||||||
z 3;0 9 3 6 , т.е. z 3;0 6; |
z 0;3 9 3 6 , т.е. z 0;3 6; z 0;0 0 . |
|||||||||||||||||||||
|
|
Таким образом, на границах области D функция достигает наименьше- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
; |
3 |
|
|
3 |
и наибольшего значения в точках A 3;0 |
|||||||
го значения в точке M 2 |
2 |
2 |
z |
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
иB 0;3 z 6 .
3)Сравнивая значения функции в стационарной точке и в точках, в которых функция достигает наименьшего и наибольшего значений на границах области, сделаем вывод.
Наибольшее значение функции z 6 достигается в точках A 3;0 и
B 0;3 .
Наименьшее значение функции z 1 достигается в стационарной точке M1 1;1 .
Ответ: наибольшее значение z 6 в A 3;0 и B 0;3 , наименьшее значение z 1 в M1 1;1 .
2.15.3 Условные экстремумы
При отыскании экстремумов функций нескольких переменных часто возникают задачи, связанные с так называемым условным экстремумом.
Рассмотрим функцию
z f x1, x2 ,..., xm f M , |
(2.15.1) |
при условии, что её аргументы являются независимыми переменными, а связаны между собой k соотношениями k m :
|
i x1 , x2 ,..., xm 0 i |
|
. |
(2.15.2) |
|
1, k |
|||
Соотношения (2.15.2) называются условиями связи. Пусть координаты |
||||
точки M0 |
x10, x20 ,..., xm0 удовлетворяют уравнениям (2.15.2). |
|
||
Определение. Функция (2.15.1) имеет в точке M 0 условный минимум (максимум) при условиях связи (2.15.2), если существует такая окрестность точки M0 , что для любой точки M x1 , x2 ,..., xm M M0 этой окрестности,

257
координаты которой удовлетворяют уравнениям (2.15.2), выполняется неравенство f M f M0 f M f M0 .
Другими словами, условный максимум (минимум) – это наибольшее (наименьшее) значение функции в точке M0 по отношению не ко всем точ-
кам из некоторой окрестности точки M0 , а только к тем из них, которые свя-
заны между собой условиями связи.
Рассмотрим более подробно понятие условного экстремума на примере функции двух переменных.
Пусть задана функция z f x; y и линия L на плоскости XOY . Задача состоит в том, чтобы на линии L найти такую точку M x, y , в
которой значение функции z f x; y является наибольшим или наимень-
шим по сравнению со значениями этой функции в точках линии L , находящихся вблизи точки M x, y . В отличии от обычной точки экстремума, зна-
чение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой её окрестности, а только в тех, которые лежат на линии L .
Совершенно ясно, что точка обычного экстремума является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное утверждение не всегда верно, т.е. точка условного экстремума может
и не быть точкой обычного экстремума. |
|
|
|
|
|||
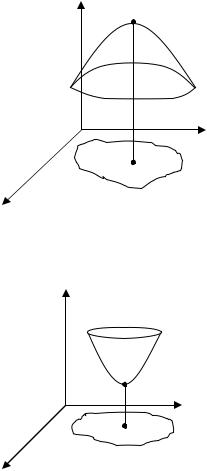
Например, функция z |
1 x2 y2 имеет максимум в точке O 0;0 . |
||||||
Ему соответствует вершина P полусферы (см. рис. 2.15.5). |
|
|
|
|
|||
|
|
|
Если линия L есть прямая, проходящая через |
||||
z |
|
точки |
A и B (её уравнение x y 1), то геометри- |
||||
M |
|
чески ясно, что для точек этой линии наибольшее |
|||||
|
|
||||||
|
M1 |
|
|
1 |
; |
1 |
|
|
|
значение функции достигается в точке M |
2 |
2 |
, |
||
|
|
|
|
|
|
||
|
P |
B y |
лежащей посередине между точками A и B . Это и |
|||
|
||||||
A |
|
есть точка |
условного |
экстремума |
(максимума) |
|
|
|
|||||
x |
|
|
функции z |
1 x2 y2 |
на данной линии; ей соот- |
|
рис. 2.15.5 |
|
|||||
|
ветствует точка P1 на |
полусфере и |
из рисунка |
|||
|
|
|
||||
2.15.5.видно, что ни о каком обычном экстремуме здесь не может быть речи.
Взаключительной части задачи об отыскании наибольшего и наименьшего значений функции в замкнутой области (см. п. 2.15.2) нам приходится находить экстремальные значения функции на границе этой области, т. е. на какой-то линии, а следовательно, решать задачу на условный экстремум.

258
На практике для отыскания условных экстремумов удобно использовать метод множителей Лагранжа, алгоритм которого состоит в следующем:
1. Составить функцию Лагранжа L x; y f x; y x; y , где –
неопределенный постоянный множитель.
2. Найти экстремум функции Лагранжа, сведя необходимые условия
|
|
|
|
|
0, |
|
|
Lx fx |
x |
||
экстремума к системе трех уравнений: |
|
|
|
0, с тремя неиз- |
|
L |
y fy |
y |
|||
|
|
|
x; y 0. |
|
|
|
|
|
|
||
вестными x, y, и определив эти неизвестные, тем самым найти стационар-
ные точки.
3. Найти определитель матрицы Гессе
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L |
L |
, т. е. G |
L |
L |
|
, во всех. |
||
G |
xx |
xy |
|
xx |
xy |
|
||
|
Lxy |
|
|
|
Lxy |
Lyy |
|
|
|
Lyy |
|
|
|
||||
4.Сделать выводы на основании следующих заключений:
–если G 0 , то функция z f x; y имеет условный экстремум при усло-
виях связи (2.15.2), а именно:
при Lxx 0 – условный минимум, при Lxx 0 – условный максимум;
–если G 0 , то условного экстремума нет;
–если G 0 , то требуются дополнительные исследования.
Пример. Найти экстремум функции z 6 4x 3y при условии, что
переменные x и y удовлетворяют уравнению x2 y2 1.
Решение:
1)Составим функцию Лагранжа L x; y 6 4x 3y x2 y2 1 .
2)Найдем Lx и Ly и найдем стационарные точки (точки подозритель-
ные на экстремум), решив следующую систему уравнений: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Lx |
4 2 x 0 |
|
|
2x |
|
|
x |
|
2 3 |
|
|
|
|
|
|
3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
x |
|
|
|
|
4 y 3x |
|
y |
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
2 y |
4 |
|||||||||||||||||
Ly |
3 2 y 0 |
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x2 y2 |
1 |
|
|
|
|
|
|
2 |
y |
2 |
1 |
x2 y2 1 |
|
2 |
y |
2 |
1 |
||||||||||
|
|
|
2 |
|
|
2 |
|
|
x |
|
|
|
|
x |
|
|
|||||||||||||
|
|
|
|
|
y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
9 |
x2 1, 25 x2 1, x |
|
16 |
4 , x |
4 |
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
16 |
|
16 |
|
|
|
|
|
|
|
25 |
5 |
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
