Добавил:

dansnpa Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт фундаментальной биологии и биотехнологии СФУ

Предмет:

Математические методы в биологии

Файл:

Конспект лекций Высшая математика (Басканова)

.pdf

Скачиваний:

150

Добавлен:

17.01.2018

Размер:

5.08 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 7021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

199

Тогда, lim y lim f x x 0 , т.е. бесконечно малому прира-

x 0 x 0

щению аргумента соответствует бесконечно малое приращение функции, а значит, функция непрерывна в данной точке. Ч. И т.д.

Замечание. Обратное утверждение не всегда верно, т.е. если функция непрерывна в точке, то она может быть не дифференцируемой в этой точке.

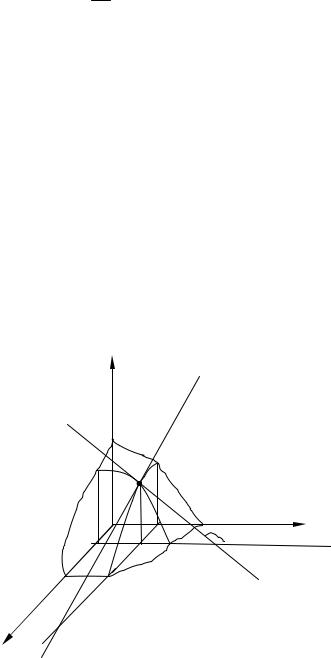
Пример. y 3 x	– непрерывна на интервале ; (см. рис. 2.7.4).
Её производная:	y		1		в точке x 0 не существует, следователь-
		3	x	2
	3

но, функция не дифференцируема.

2	y	3 x
2
-8		x
1	8	x

рис. 2.7.4

Определение. Если функция y f x имеет непрерывную производную y f x на некотором интервале a; b , то функция называется глад-

кой.

Теперь рассмотрим функцию двух переменных z f x; y , определен-

ную на некоторой области D .

Так как x и y – независимые переменные, то одна из них может изме-

няться, а другая сохранять свое значение. Проделаем следующие операции:

–независимой переменной x дадим приращение x , сохраняя значение y неизменным;

–найдем соответствующее приращение функции zx – частное при-

- f x; y ;ращение x

– найдем среднюю скорость изменения значения функции в направлении координатной оси OX на интервале x , равную

zx f x x; y f x; y ;

x x

– найдем скорость изменения функции в точке в направлении оси OX , перейдя в последнем равенстве к пределу при x 0

lim	zx lim		f x x; y f x; y	zx .
			x
x 0	x	x 0

200

Аналогично можно найти частное приращение функции по переменной y : zy f x; y y f x; y , и получить скорость изменения функции в точке в направлении оси OY :

lim	zy	lim	f x; y y f x; y	zy .
	y		y
y 0		y 0

Определение. Если существует предел отношения частного приращения функции в точке M к соответствующему приращению независимой переменной при стремлении последнего к нулю, то он называется частной производной функции в точке M по данной независимой переменной.

Обозначается zx , xz ; zy , yz .

zx lim

z y

lim

z y

x 0

y 0

Аналогично для функции n – независимых переменных

u f x1, x2,..., xk :

lim

x 0

Таким образом, функция двух переменных имеет две частные производные, а функция n переменных z f x1 , x2 ,..., xn будет иметь n частных

производных.

Из определения частных производных следует, что частная производная находится в предположении, что изменяется только одна независимая переменная, а остальные остаются постоянными.

Графиком функции z f x; y является некоторая поверхность (см.

		l1
l2
z=f(x0;y)		z=f(x;y0)
z=f(x0;y)		M0
	0	y0	y
x0	0		β
			β

αрис. 2.7.5

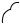
201

рис.2.7.5). График функции z f x; y0 есть линия пересечения этой поверхности с плоскостью y y0 . Исходя из геометрического смысла производной

для функции		одной	переменной (см.			выше)	делаем	вывод,	что
fx x0; y0 tg , где – угол между осью OX и касательной 1 проведенной
к кривой	z f x; y0		в	точке	касания	M 0 x0 ; y0 ; z0 .		Аналогично,
fy x0; y0 tg , где – угол между осью OY						и касательной 2 проведенной
к кривой z f x0 ; y в точке M 0 . Это и есть геометрический смысл част-
ных производных функции двух переменных.
Прямые 1		и 2 определяют плоскость P , которая называется каса-
тельной плоскостью			к	поверхности, являющейся графиком функции
z f x; y	в точке M 0 , значит, координаты всех точек прямых 1 и 2								удов-
летворяют уравнению этой плоскости.
Используя геометрический смысл частных производных и уравнение
плоскости,		проходящей			через	точку	M 0 x0 ; y0 ; z0 :
A x x0 B y y0 C z z0 0,					можно составить уравнение плоскости
P .
Уравнение касательной плоскости:
	P : z z 0 fx x0; y0 x x0 fy x0; y0 y y0 .							(2.7.6)

Прямая, проходящая через точку M 0 и перпендикулярная касательной

плоскости, построенной в этой точке поверхности, называется нормалью к поверхности.

Используя условия перпендикулярности прямой и плоскости (см. п.1.9.2), легко получить каноническое уравнение нормали.

Уравнение нормали к поверхности

L :	x x0	y y0	z z0	.
	fx x0 ; y0	fy x0 ; y0
			1

202

ЛЕКЦИЯ 2.8. ПРОИЗВОДНАЯ СЛОЖНОЙ И ОБРАТНОЙ ФУНКЦИЙ. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ. ТАБЛИЦА ПРОИЗВОДНЫХ.

2.8.1. Производные некоторых элементарных функций

Для вывода формул производных некоторых элементарных функций будем использовать определение производной и правила дифференцирования.

Степенная функция y xn .

1. При n 1 y x

f x x , f x x x x ,

y f x x - f x x x - x x ,

y lim			y		lim		x	1.
	x 0		x		x 0		x		x 1.
					y x2 .
2. При n 2
f x x2 ,				f x x x x 2 x2 2x x x 2 ,
y f x x - f x x2 2x x x 2 - x2 2x x x 2 ,
	lim	y		lim		2x x x 2			x 2x x	lim 2x x 2x.
y		x					x	lim	x
	x 0				x 0			x 0		x 0

					y x3			x2 2x .
3. При n 3
f x x3 ,				f x x x x 3 x3 3x2 x 3x x 2 x 3,

y f x x f x x3 3x2 x 3x x 2 x 3 x33x2 x 3x x 2 x 3 ,

	lim	y	lim	3x2 x 3x x 2 x 3			x 3x2 3x x x 2
y	lim	x	lim		x	lim	x
	x 0	x	x 0		x	x 0	x
	lim 3x2 3x x x 2				3x2,
	x 0
							3x2
	и т.д., тогда					x3	3x2
	и т.д., тогда

						x n n xn-1 .
	Логарифмическая функция y loga x .
	1.	f x loga x ,			f x x loga x x ,

203

	x x log	x x			x
y log		x log		log 1	,
			x
a	a	a		a	x

log

loga 1

y lim

lim

x 0

1 loga e 1

ln e

xln a

ln a

loga x

2. При a e ,

y ln x ,

x ln a

f x ln x , y f x x - f x ln x x - ln x ,

ln 1

1 ,

y lim

lim

x 0 x

x 0

x x

ln x

x .

Тригонометрические функции

y sin x

y f x x f x sin x x sin x

sin x cos x cos x sin x sin x sin x 1 cos x cos x sin x,

y lim

sin x

1 cos x

lim

cos x sin x

lim

x 0

x 2

sin x

lim

cos x

sin x

2 x

x 0

sin x lim

cos x lim

sin x

sin x 0 cos x 1 cos x,

x 0

cos x .

y cos x .

sin x

y f x x f x cos x x cos x

cos x cos x sin x sin x cos x cos x 1 cos x sin x sin x,

y lim

lim

1- cos x

- lim

sin x

cos x

sin x

x 0

lim

-cos x x

- lim sin x sin x -cos x lim

- sin x lim sin x

x 0

2 x

x 0

x 0 x

cos x 0 -1 sin x

-sin x,

204

cos x

sin x .

y tgx sin x .

cos x

По правилу дифференцирования 5 п. 2.7.2:

sin x

cos xcos x sin x sin x

sin x

cos x sin x cos x

cos2 x

cos

cos x

cos2 x sin2 x

cos2 x

cos2

tgx

cos x

cos2 x

y ctgx

Аналогич-

sin x

cos x

sin x cos x sin x

sin x sin x cos x cos x

cos x

sin2 x

но:

sin x

cos2

x sin

2 x

sin2

ctgx sin12 x .

2.8.2.Производная сложной функции

Функция y f (u) , где u u x – сложная функция с промежуточным

аргументом u и одной независимой переменой x .
Теорема 1. Если функция u u x имеет производную ux в точке x , а
функция	y f (u)		имеет	производную	yu	в соответствующей		точке
u u u x , то сложная функция y f u x					имеет производную		yx	в точке
x , которая находится по формуле
				yx yu ux .
Доказательство: По условию теоремы
1.	lim	y yu	, отсюда, на основании теоремы 7 п.2.3.3
u 0		u	y
			y	yu или y yu		u u ,		(2.8.1)
			u

где 0 при u 0.

205

lim

ux , поэтому u ux x x , где 0 при x 0.

x 0

u x x x u x x x ,

Подставляя u в (2.8.1), получим: y yu

т.е. y yu u x x yu x u x x

x ,

y yuux yu ux .

В последнем равенстве, перейдя к пределу при x 0, получаем

lim

lim yuux yu ux yu ux .

x 0

Таким образом,

yx yu

ux . Ч. и т. д.

Пример.

y sin 2

x : y u 2 , где u sin x ,

yx yu ux 2u sin x 2sin x cos x .

Замечание. Если промежуточных аргументов несколько теорема 1 ос-

тается в силе. Так, если y f (u) ,

u u и x , то

yu u x .

Пример.

y ctg 2x 15 3 :

y ctgu , u 3

и 2x 15.

3v 2x 15

3 2x 15 2

yx yu

sin2 u

sin2 v3

15 .

sin2 2x 15 3

z f u, , где u u x; y ,

Рассмотрим

функцию двух переменных

x; y . Тогда

z f u x; y , x; y –

сложная функция независимых пе-

ременных x и y .

Теорема 2. Если z f u, – дифференцируемая функция и u u x; y ,

x; y

– дифференцируемые функции независимых переменных x и y ,

то производная сложной функции z

по каждой независимой переменной x и

y равна сумме произведений частных производных этой функции по ее про-

межуточным переменным u и на их производные по соответствующей независимой переменной x и y .

z z u z ,

x u x x

z z u z .

y u y y

(2.8.2)

(2.8.3)

206

Пример. Дана функция z u 2 3 ,

где u y tg3x

и 3

y x2 .

Найти xz , yz .

Решение: Найдем xz , используя формулу (2.8.2).

Предполагая, что u – свободная переменная, а const , найдем uz :

0 2 .

Предполагая, что

– свободная переменная, а u const , найдем

2u 3.

2x ,

Теперь

найдем

тогда

cos2 3x

2u 3 2x .

cos2 3x

Найдем

, используя формулу (2.8.3).

известны. Теперь

найдем

u tg3x ,

, тогда

z 2tg3x 2u 3

33 y2

33 y 2

Ответ:

2 3y

2x 2u 3 ,

2tg3x 2u 3 .

cos2 3x

Теорема 3.

Если z f x; y

дифференцируемая функция и x x t ,

y y t

дифференцируемые функции независимой переменной t ,

то произ-

водная сложной функции z t f x t ; y t вычисляется по формуле

z dy .

(2.8.4)

y y x –

Следствие.

Если z f x; y

дифференцируемая функция и

дифференцируемая функция

независимой

переменной x , то производная

сложной функции z f x; y x вычисляется по формуле

z dy .

(2.8.5)

2.8.3. Производная обратной функции

207

Пусть y f x и x y – взаимно обратные функции.

Теорема 4. Если функция				y		f x	строго монотонна на интервале
a; b и имеет производную	f	x 0				в произвольной точке				x a;b , то об-
ратная ей функция x y
										в соответствую-
	также имеет производную y
щей точке, которая вычисляется по формуле								1
y			1		или xy				.	(2.8.6)
			f x
								yx

Доказательство: Рассмотрим обратную функцию x y . Дадим ар-

гументу y приращение y 0. Ему соответствует приращение x обратной функции. Так как y f x – строго монотонная, то x 0 . И поэтому можно

записать x

функции x 0 при

y 0

силу

непрерывности

обратной

lim

f x 0 (по условию), тогда

x 0

lim

y 0

y 0 y

lim

x 0

. Что и требовалось доказать.

Значит y

f x

Пример. Найти производные обратнотригонометрических функций и

показательной функции.

y arcsin x ,

x sin y : yx

cos y

1 sin2

1 x2

arcsin x

1 x2

y arccos x ,

x cos y : yx

sin y

1 cos2 y

1 x2

arccos x

1 x2

y arctgx ,

x tgy :

cos2

tg 2 y

cos2 y

arctgx

1 x2

			208
4. y arcctgx , x ctgy : yx		1							1				sin2 y			1		1	,
4. y arcctgx , x ctgy : yx		xy								1			sin2 y		1	ctg2 y	1	x2	,
										1
									sin2 y
									sin2 y
												1
	arcctgx													.
	arcctgx											1 x2		.
5. y a x , x loga y : yx		1							1		y ln a a x ln a ,
5. y a x , x loga y : yx		xy							1		y ln a a x ln a ,
		xy							1
								y ln a
									a x ln a .
			a x						a x ln a .
6. y e x , x ln y : yx	1		1				y ex ,
6. y e x , x ln y : yx				1			y ex ,
	xy			1
					y
										ex .
						ex				ex .

2.8.4. Таблица производных

На практике чаще всего приходится находить производные от сложных функций, поэтому в приведенной ниже таблице формул дифференцирования

аргумент x заменен на промежуточный аргумент u .

x 1

9. sin u

cosu

n 1

10.

sin u

cosu

11.

tgu

cos

12.

ctgu

sin

au ln a

13.

arcsin u

1 u2

eu u

14.

arccosu

1-u2

loga u

15.

arctgu

u ln a

1 u2

ln u

16.

arcctgu

1 u2

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 7021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>