7. Заданы множества M={9,5,4} и N={9,1,4,2,5,3}, тогда для них верным утверждением будет:
a)«Множество M есть подмножество множества N»;
b)«Множества M и N не имеют общих элементов»;
c)«Множества M и N равны»;
d)«Множество M включает в себя множество N».
8. Заданы множества A={5,1,9,3} и B={9,3,5,1}, тогда для них верным утверждением будет:
a)«Множества A и B равны»;
b)«Множества A и B не имеют общих элементов»;
c)«Множество A включает в себя множество B»;
d)«Множество A есть подмножество множества B».
Практическое занятие №2. Алгебра множеств
1. Цель работы
Цель работы – Уметь выполнять алгебраические действия с множествами.
2. Теоретический материал для практического занятия №2. Алгебра множеств. Операции над множествами
2.1. Операции над множествами
Суммой (или объединением) двух множеств называется третье множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В. Сумма двух множеств записывается: С=А В. Объединение множеств А и В обозначается:
A B ={x | x A или x B}.
Пример.
а) Пусть А = {1, 2, 3}, В = {3, 4, 5}. Тогда А В = {1,2,3, 4, 5}.Таким образом, если элемент x принадлежит объединению А В, то он может принадлежать или множеству А, или множеству В, или обоим этим множествам.
Пересечение множеств А и В есть множество, состоящее из элементов, общих для обоих множеств. Пересечение множеств обозначается:
A ∩B ={x | x A и x B} .
Пример.
Пусть А = {1, 2, 3}, В = {3, 4, 5}. Тогда А∩В = {3}.
В результате можно сделать вывод, что А∩В А, А∩В В и А∩В А В.
Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество.
Пример Пусть А = {7,9,5}, В = {2, 4,6}. Тогда А∩В = .
Разностью двух множеств А и В называется новое множество, все элементы которого являются элементами множества А, но не являются элементами множества В. Обозначается:
12
A \ B ={x | x A ; x B};
Пример А = {1, 2, 3, 4}, В = {3, 4, 5, 6}. Тогда А \ В = {1, 2}, В \ А= {5, 6}.
Если рассматриваемое множество В является подмножеством некоторого фиксированного множества А, то разность А\В называется дополнением множества В или дополнением до А множества В.
Разбиением множества Х называется такая расчлененная система U-непустых подмножеств множества Х, что каждый элемент множества Х является элементом некоторого множества системы U. Пример. Множество U={{1,2},{3,4},{5,6},{7,8}} есть результат операции разбиения множества X={1,2,3,4,5,6,7,8}. Данная операция позволяет образовать новое множество U из одного существующего множества X. Можно выделить такое множество, что все рассматриваемые предметы являются его элементами. Такое множество называется универсальным. Обычно универсальное множество обозначается U.
Дополнением множества А называется множество A ,состоящее из элементов множества U,не являющихся элементами множества А: A ={x U| x A}.
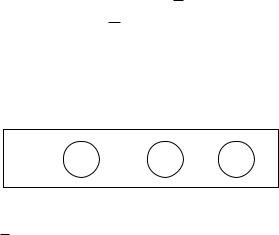
На диаграмме Эйлера - Венна универсальное множество обозначают в виде прямоугольника и буквы U:
Множества, входящие в универсальное множество, обозначают в виде кругов внутри прямоугольника (рис.1).
U
A B C
Рис. 1.
Разность между универсальным множеством U и множеством А называется дополнением множества А. Обозначается: A = U \ A .
2.2. Геометрическая интерпретация алгебры множеств
Пример 1. Универсальное множество состоит из 33 строчных букв русского алфавита Заданы множества A, B, C . Найти множества X и Y и вычислить их мощность (количество элементов в множествах) .
Пусть даны множества: А{фпдкш}; В{чмпуш}; C{аючкмтф}.
Требуется найти множества X=(A \ C) U (B\C); Y=(A \ C) ∩ (B\C);
Решение.
A \ C={пдш} (B\C)={пуш}; Х={пдуш}; Y={пш};
Мощность множества X =4. Мощность множества Y=2.
С помощью диаграмм Эйлера – Венна можно иллюстрировать операции над множествами
(рис. 2).
13