X |
-3 |
2 |
P |
0,3 |
0,8 |
Тогда математическое ожидание M(X) этой случайной величины равно …
-1,1
-2,5
-1
-0,7
5. Дискретная случайная величина X имеет закон распределения вероятностей:
X |
-1 |
2 |
P |
0,3 |
0,7 |
Тогда математическое ожидание M(X) этой случайной величины равно …
-0,4
-1,1
-2
-1,7
6. Дискретная случайная величина X имеет закон распределения вероятностей:
X |
-2 |
3 |
P |
0,4 |
0,7 |
|
|
|
Тогда математическое ожидание M(X) этой случайной величины равно …
-1
-2,9
-1,3
-1,1
Практическое занятие №8. Непрерывные случайные величины. Законы распределения
1. Цель работы
Цель работы – усвоить понятие непрерывной случайной величины, законы ее распределения, характеристики. Научиться находить вероятность непрерывной случайной величины. Выработать навыки вычисления основных характеристик непрерывной случайной величины.
2. Теоретический материал для практического занятия №8
2.1. Функция распределения и плотность вероятности непрерывной случайной величины
Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.
Случайная величина называется непрерывной, если существует неотрицательная функция f(х), удовлетворяющая при любых х равенству:
|
Х |
|
|
|
|
∫ f (x)dx |
. |
|
(24) |
F(х)= −∞ |
|
|
||
Функция f(х) называется плотностью вероятности: |
|
|
|
|
lim |
P(x < Х < x + x) |
. |
(25) |
|
f(х) = x→0 |
x |
|
|
|
37
Непрерывная случайная величина задается либо функцией распределения F(х) (интегральным законом распределения), либо плотностью вероятности f(х) (дифференциальным законом распределения).
Функция распределения F(х)=Р(Х<х), где х – произвольное действительное число, дает вероятность того, что случайная величина меньше х.
Функция распределения F(х) имеет следующие свойства: 1) Р(а ≤ Х < в) = F(в) - F(а);
2)
F( х1 ) ≤ F( х2 ), если х1 < х2; |
(26) |
lim F (x)
3) x→+∞ =1;
lim F (x)
4) x→−∞ = 0.
Плотность вероятности f(х) (дифференциальный закон распределения) обладает следующими основными свойствами:
1) f(х) ≥ 0.
Геометрически это означает, что вся кривая распределения лежит не ниже оси абсцисс; dF(x)
2) f(х) = dx = F′(х);
3)
∞ |
|
∫ |
(27) |
−∞ |
f(х)dх = 1. |
Геометрически это означает, что полная площадь, ограниченная кривой распределения и осью абсцисс равна единице;
4)
b |
|
|
∫ |
(28) |
|
Р(а ≤ Х < в) = a |
f(х)dх . |
|
Геометрически вероятность попадания величины Х на участок (а, b) равна площади кривой распределения, опирающейся на этот участок.
Функция распределения связана с плотностью следующими формулами:
x |
|
|
|
∫ |
f(t)dt, |
(29) |
|
F(х) = −∞ |
|
||
dF(x) |
|
(30) |
|
f (х) = dx |
= F′ (х). |
||
|
2.2. Основные характеристики (параметры распределения) непрерывной случайной величины
Свойства случайной величины могут характеризоваться различными параметрами. Важнейшие из них - математическое ожидание случайной величины, которое обозначается через М(Х), и дисперсия D(Х) = σ2(Х), корень квадратный из которой σ (Х) называют среднеквадратическим отклонением или стандартом .
2.2.1. Математическое ожидание
Математическим ожиданием непрерывной случайной величины Х называется интеграл:
38
∞ |
|
∫ |
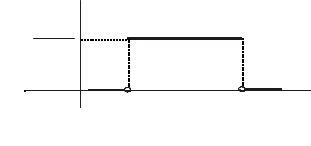
(31) |
М(Х) = −∞ х f(х)dх,
где f(х) - плотность вероятности распределения случайной величины Х.
Математическое ожидание М(Х) можно понимать как «теоретическое среднее значение случайной величины».
2.2.2. Дисперсия
Если математическое ожидание случайной величины дает «ее среднее значение» или точку на координатной прямой, «вокруг которой разбросаны» значения рассматриваемой случайной величины, то дисперсия характеризует «степень разброса» значений случайной величины около ее среднего.
Для непрерывной случайной величины Х:
∞ |
|
∫ |
(32) |
D(Х) = −∞ { x - M(X)}2 f(x)dx.
2.3. Некоторые частные распределения
Следует рассмотреть некоторые важные для практики распределения случайных величин и соответствующие им числовые характеристики.
2.3.1. Равномерное распределение
Непрерывная случайная величина X называется распределенной равномерно на отрезке [a,b], если ее плотность распределения вероятностей постоянна на данном отрезке:
0, |
|
|
x [a,b] |
|
|
|
1 |
|
. |
(33) |
|
f (x) = |
|
||||
|
|
|
, |
x [a,b] |
|
|
−a |
|
|||
b |
|
|
|
||
Функция распределения в этом случае согласно (21) ,примет вид:
|
0, |
|
x < a |
|
x −a |
|
|
|
|
F(x) = |
|
, |
a ≤ x <b. |
(34) |
|
||||
b −a |
|
x ≥b |
|
|
|
1, |
|
|
|
Это распределение реализуется, например, в эксперименте, в котором наудачу ставится
точка на отрезок [a,b], при этом случайная величина X – абсцисса поставленной точки.
На рис. 6 представлен график функции р(х) случайной величины, равномерно распределенной на промежутке [a;b]
p(x)
1 c = b - a
x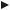
Рис.6. График функции р(х) случайной величины, равномерно распределенной на промежутке [a;b]
Примером равномерно распределенной непрерывной случайной величины Х является ошибка при округлении отсчета до ближайшего целого деления шкалы измерительного прибора, проградуированной в некоторых единицах.
39