Модуль II Основы комбинаторики Лекция 6 Основные понятия комбинаторики

План лекции

1. Правила суммы и произведения

2. Выборки

3. Метод включений и исключений

Ключевые слова: выборка, правило суммы, правило произведения, размещения, сочетания, перестановки, разбиения, формула включений и исключений.

1 Правила суммы и произведения

Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому целями комбинаторного анализа являются изучение комбинаторных конфигураций, алгоритмов их построения, оптимизация таких алгоритмов, а также решение задач перечисления. Простейшими примерами комбинаторных конфигураций являются перестановки, размещения, сочетания и разбиения. При подсчете комбинаторных конфигураций используются правила суммы и произведения.

Правило суммы

Если все изучаемые комбинации удается разбить на несколько классов, таких, что каждая комбинация входит в один и только один класс, то общее число комбинаций равно сумме чисел комбинаций во всех классах. Это утверждение, принимаемое в качестве аксиомы, называют правилом суммы. Его же можно сформулировать иначе:

Если множество А есть m-множество, а множество В есть n-множество, причем эти множества не имеют общих элементов и т + п = p, то их объединение А и В есть p-множество.

Коротко правило суммы может быть записано следующим образом:

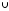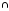|А В| = |А|+ |В|, А В =Ø.

Отметим, что указанное правило теряет силу, если некоторые из эле­ментов m-множества А и n-множества В совпадают, то есть А 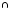B не пусто. В этом случае их объединение содержит - т + п -к элементов, где к — число совпадений, то есть

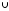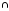|А В| = |А|+ |В| - |А В|.

Используя принцип математической индукции, из этого соотношения легко вывести общее правило суммы для конечного семейства множеств.

Правило произведения

Если объект а можно выбрать m способами, а после каждого такого выбора можно выбрать п способами объект, то выбор обоих объектов а и b в указанном порядке можно осуществить mn способами.

2 Выборки

Совокупность (a₁,a₂,...,a_r) элементов (не обязательно различных) некоторого n-множества называется выборкой объема r из п элементов, или (п, r)-выборкой, или r -выборкой.

Выборка называется упорядоченной, если в ней задан порядок следования элементов, т. е. известно, какой элемент является первым, какой — вторым и т. д. Если такой порядок не определен, то выборка называется неупорядоченной.

Пусть дано множество М = {a₁,a₂,...,a_n}. Перестановкой элементов множества М называется любая последовательность (a_i1,a_i2,...,a_in), состоящая из n различных элементов множества М.

Перестановки отличаются друг от друга только порядком входящих в них элементов. Покажем, что число Р_n всех перестановок множества М равно n!.

Р_n = n!.

Пусть М – множество, состоящее из n элементов, m ≤ n. Размещением из n элементов по m или упорядоченной (n,m)-выборкой, называется любой кортеж (а_i1,a_i2,…,a_im), состоящий из m попарно различных элементов множества М..

Число размещений из n по m обозначается через A^m_n или P(n,m).

Сочетанием из n элементов по m или неупорядоченной (n,m)-выборкой, называется любое подмножество множества М, состоящее из m элементов.

Число сочетаний из n по m обозначается через С_n^m или С(n,m).

Числа С_n^m называют биномиальными коэффициентами.

Размещением с повторением из n элементов по m или упорядоченной (n,m)-выборкой с возвращениями называется любой кортеж (а₁,…,а_m) элементов множества М, для которого |M| = n.

Поскольку в кортеже (а₁,а₂,…,а_m) на каждое место может претендовать любой из n элементов множества М, число размещений с повторениями

.

Сочетанием с повторением из n элементов по m или неупорядоченной (n,m)-выборкой с возвращениями называется множество, которое состоит из элементов, выбранных m раз из множества М, причем один и тот же элемент допускается выбирать повторно.

Число сочетаний с повторениями из n элементов по m обозначается через С(n,m) и вычисляется по формуле

Пусть М – множество мощности n, {M₁,M₂,...,M_k} – разбиение множества М на k подмножеств, |M_i| = m_i, m₁ + m₂ + ... + m_k = n. Кортеж (M_1,…,M_k) называется упорядоченным разбиением множества М.

Число R(m₁,m₂,…,m_k) упорядоченных разбиений (M₁,M₂,...,M_k), для которых |M_i| = m_i, равно , а числоR(n,k) упорядоченных разбиений на k подмножеств вычисляется по формуле

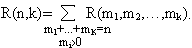
Числа R(m₁,m₂,…,m_k) называются полиномиальными коэффициентами.

Число R(m₁,m₂,…,m_k) разбиений исходного множества М на k подмножеств М₁,М₂,...,М_k, |M_i| = m_i, неупорядоченных между собой, вычисляется по формуле

а число всех возможных разбиений множества М на k подмножеств неупорядоченных между собой, равно