3 Покрывающие деревья (остовы)

Цикломатическим числом неориентированного графа G называется величина γ(G) = т - п + k, где т - число ребер, п - число вершин, k — число связных компонент. Для дерева и леса γ (G) = 0, для других графов γ (G) > 0.

Остовом, или покрывающим деревом, связного графа G=(V, E) называется часть G, которая содержит все его вершины и является деревом. Хордой остова графа G называется ребро G, не принадлежащее остову.

Очевидно, что любой связный граф имеет хотя бы один остов, а любой несвязный граф остова не имеет.

В последующем алгоритме части исходного графа G, которые возникают в процессе построения покрывающего дерева, будем называть букетами.

Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g

1. Выбрать любое ребро G, не являющееся петлей. Пометить его меткой α и объявить букетом это ребро вместе с его концевыми вершинами.

2. Выбрать любое непомеченное ребро G, не являющееся петлей:

а) если один из концов выбранного ребра принадлежит построенному ранее букету В, а другой конец свободен (не принадлежит ни одному букету), пометить выбранное ребро меткой α, включить его вместе со свободным концом в букет В и перейти к шагу 3;

б) если оба конца выбранного ребра свободны, поме­тить его меткой а, объявить это ребро вместе с его конце­выми вершинами новым букетом и перейти к шагу 3;

в) если концы выбранного ребра принадлежат разным построенным ранее букетам В и С, пометить выбранное ребро меткой α, включить его и букет С в букет В и перейти к шагу 3;

г) если оба конца выбранного ребра принадлежат одному букету, пометить его меткой β и перейти к шагу 3;

д) если непомеченных ребер нет, закончить алгоритм.

3. Если все вершины графа G вошли в один букет, закончить алгоритм. Если нет, перейти к шагу 2.

Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g

1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G₂ графа G. Положим i:=2.

2. Если i=n(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).

3. Строим граф G_i+1. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i+1 и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2.

Лекция 12 Двудольные и планарные графы

План лекции

1. Двудольные графы

2. Планарные графы

Ключевые слова: двудольный граф,k-дольный граф, паросочетание, плоский граф, укладка, планарный граф, грань.

1 Двудольные графы

Двудольным графом G=(X, Y, Е) называется неориентированный граф, вершины которого можно разбить на два класса X и Y так, что концы каждого ребра принадлежат разным классам. Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли, полный двудольный граф принято обозначать символом 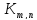гдет = |Х|, n = .

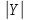Введенные понятия допускают естественное обобще-ие. Неориентированный граф называется k-дольным, если его вершины можно разбить на k классов так, что концы каждого ребра принадлежат разным классам. Полный k-дольный граф — это k-дольный граф, в котором каждая вершина одной доли соединена с каждой вершиной всех остальных долей.

Пример. На рисунке 24 представлены двудольный граф G=(X, Y, Е), полный двудольный граф К_3,3 и трехдольный граф G=(X, Y, Z, Е), где X = {х₁ x₂}, Y = {у₁ y₂, y₃}, Z = {z₁ z₂}.

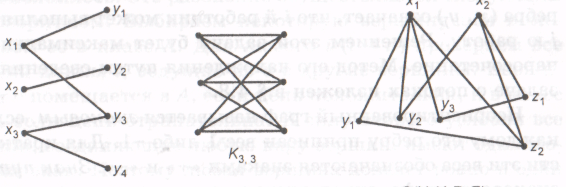
G=(X, Y, Е) G=(X, Y, Z, Е)

Рисунок 24 – Двудольные графы

Теорема. Граф является двудольным, если и только если длины всех его простых циклов четны.

Паросочетанием в неориентированном графе называется множество попарно несмежных ребер. Задача о максимальном паросочетании заключается в нахождении паросочетания максимальной мощности. Для двудольного графа одной из наиболее известных интерпретаций задачи о максимальном паросочетании является задача о назначениях, которая заключается в следующем. Имеется т работников и п работ. Каждый работник способен выполнять несколько работ; каждую работу могут выполнять несколько работников. Требуется определить назначения по принципу «один работник - одна работа» так, чтобы загрузить максимальное число работников.

Условия этой задачи представляются в виде двудольного графа, в котором вершины класса X соответствуют работникам, вершины класса Y- работам, а наличие ребра (x_i, y_j) означает, что i-й работник может выполнять j-ю работу. Решением этой задачи будет максимальное паросочетание, которое находится путем сведения к задаче о потоках.