Лекция 5 Свойства и виды бинарных отношений

План лекции

1. Свойства бинарных отношений

2. Виды бинарных отношений

Ключевые слова: рефлексивное, симметричное, антирефлексивное, антисимметричное, транзитивное отношение, отношение эквивалентности, отношение порядка, разбиение множества.

1 Свойства бинарных отношений

Бинарное отношение R, определенное на множестве А, называется:

- рефлексивным, если для любого 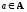aRa;

- антирефлексивным, если для любого 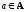не выполняетсяaRa;

-симметричным, если для любых 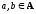из аRb следует bRa;

- антисимметричным, если аRb и bRa влекут a=b.

- транзитивным, если для любых 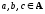изaRb и bRс следует аRс.

Например, отношение ≤ на множестве R действительных чисел, а также отношение включения подмножеств некоторого множества являются рефлексивными и транзитивными, но не являются симметричными. Отношение < на множестве действительных чисел транзитивно, но не рефлексивно, не симметрично. Отношение «х является матерью у» не рефлексивно, не симметрично, не транзитивно.

2 Виды бинарных отношений

Определение. Бинарное отношение R, определенное на множестве А, называется отношением эквивалентности или просто эквивалентностью на множестве А, если R рефлексивно, симметрично и транзитивно.

Примеры отношений эквивалентности:

1. отношение равенства в произвольной системе множеств;

2. отношение равночисленности, т.е. иметь одинаковое число элементов, в системе конечных множеств;

3. отношение «учиться в одной группе» в множестве студентов лесопромышленного факультета;

4. пусть F: A → B — отображение. Отношение σ, определяемое следующим образом: 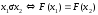, является отношением эквивалентности наА. Оно называется ядерной эквивалентностью отображения F.

Пусть σ — отношение эквивалентности на множестве А, и пусть .

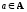Определение. Множество всех таких элементов 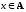, чтохσа истинно, называют смежным классом множества А по эквивалентности σ, или классом эквивалентности, и обозначают [а]_σ.

Теорема 1. Свойство I: 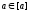. Свойство II: еслиaσb, то [а] = [b].

Лемма. Любые два смежных класса множества А по эквивалентности σ либо не пересекаются, либо совпадают.

Из леммы вытекает, что различные смежные классы не имеют общих элементов.

Определение. Совокупность всех различных смежных классов множества А по эквивалентности σ называется фактор-множеством множества А по эквивалентности σ и обозначается А/σ.

Определение. Каноническим отображением множества А на фактор-множестве А/σ по эквивалентности σ называется отображение, которое каждому элементу 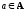ставит в соответствие содержащий его смежный класс [a]_σ.

Очевидно, это каноническое отображение сюръективно.

Отношения эквивалентности произвольного множества тесно связаны с понятием разбиения этого множества.

Определение. Разбиением (или расслоением) множества А называется система S непустых подмножеств множества А таких, что каждый элемент из А принадлежит одному и только одному подмножеству из системы S.

Подмножества из S называются смежными классами (или слоями) разбиения S.

Рассмотрим связи между отношениями эквивалентности некоторого множества и его разбиениями.

Теорема 2. Если σ — отношение эквивалентности на множестве А, то совокупность всех различных смежных классов множества А по эквивалентности σ является разбиением множества А.

Теорема 3. Пусть S — разбиение множества А, а σ — бинарное отношение на множестве А такое, что, по определению, хσу (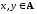) истинно тогда и только тогда, когда вS есть подмножество М, для которого 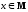,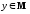. Тогда σ — отношение эквивалентности на мно­жествеА. Эта эквивалентность σ называется эквивалентностью, отвечающей разбиению S.

Теорема 4.Для любого множества А существует взаимно однозначное соответствие между множеством разбиений множества А и множеством отношений эквивалентности наА.

Определение. Бинарное отношение ρ, определенное на множестве А, называется частичным порядком, или отношением частичного порядка, если оно удовлетворяет следующим условиям:

1) хρх для любого 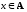(рефлексивность);

2) из хρу и yρz следует xρz для любых 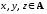(транзитивность);

3) из хρу и уρх следует х=у для любых 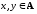(антисимметричность).

Множество А, на котором задан какой-нибудь частичный порядок, называется частично упорядоченным.

Примерами отношения частичного порядка являются: отношение 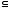включения на множестве подмножеств не­которого множества; отношение ≤ на множестве действительных чисел; отношение «х делит у» на множестве натуральных чисел.

Частичный порядок на множестве А будем обозначать символом ≤, и если a ≤ b для некоторых элементов 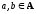, то будем говорить, чтоа меньше или равно b, а также, что а содержится в b или равно b. Если a ≤ b и а ≠ b, то будем писать а < b и говорить, что а строго меньше b или а строго содержится в b.

Определение. Элементы а, b множества А называются сравнимыми относительно частичного поряд­ка ≤ на этом множестве, если a ≤ b или b ≤ a.

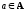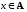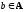Определение. Пусть А — частично упорядоченное множество с частичным порядком ≤. Элемент называется наибольшим элементом, если х ≤ а для любого . Элемент называется наименьшим элементом, если b ≤ х для любого .

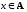Частично упорядоченное множество может обладать или не обладать наименьшим или наибольшим элементом. Однако если частично упорядоченное множество обладает наибольшим (наименьшим) элементом, то он единственный.

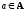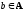Определение. Максимальным элементом частично упорядоченного множества А называется такой элемент , что каждый элементх из А либо не сравним с а, либо х ≤ а, т.е., другими словами, если А не содержит элементов, строго больших а. Минимальным элементом частично упорядоченного множества А называется такой элемент , что каждый элементx из А либо не сравним с b, либо b ≤ х, т.е. если А не содержит элементов, строго меньших b.

В отличие от наибольшего (наименьшего) элемента частично упорядоченное множество может содержать несколько максимальных (минимальных) элементов.

Лемма. Всякий наибольший элемент частично упорядоченного множества является максимальным, а всякий наименьший — минимальным.

Определение. Пусть а, b — элементы частично упорядоченного множества А. Элемент а называется непосредственно меньшим (непосредственно предшествующим) для элемента b, а b — непосредственно большим (непосредственно следующим) за а, если a < b и не существует элемента 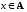, который удовлетворял бы отношениюa < х < b.

Определение. Частичный порядок на множестве А называется линейным порядком, если любые два элемента из А сравнимы относительно ≤. Множество А, на котором задан какой-либо линейный порядок, называется линейно упорядоченным множеством, или цепью. Примером линейно упорядоченного множества может служить множество всех действительных чисел с обычным отношением ≤.

Отметим, что в случае линейно упорядоченного множества его максимальный (минимальный) элемент является также наибольшим (наименьшим).

Теорема 5. Следующие свойства частично упорядоченного множества А равносильны:

1. (условие минимальности). Всякое непустое подмножество множества А является частично упорядоченным множеством, содержащим минимальные элементы;

2. (условие индуктивности). Если все минимальные элементы множества А обладают некоторым свойством Р и из того, что все элементы х из А, удовлетворяющие условию х < а, обладают свойством Р, вытекает, что элемент а также обладает свойством Р, то свойством Р обладают все элементы

Определение. Линейно упорядоченное множество, удовлетворяющее условию минимальности (а следовательно, и остальным условиям теоремы), называется вполне упорядоченным множеством.

Определение. Элемент а вполне упорядоченного множества А, не имеющий непосредственно предшествующего, называется предельным.