
- •Лесосибирск 2012
- •Лекция 1 Основные понятия теории множеств
- •1 Понятие множества
- •2 Способы задания множеств
- •3 Сравнение множеств
- •Лекция 2 Операции над множествами
- •1 Операции над множествами
- •2 Свойства операций над множествами
- •Лекция 3 Соответствия и функции
- •1 Соответствия
- •2 Функции
- •Лекция 4 Бинарные отношения и операции над ними
- •1 Понятие бинарного отношения
- •2 Операции над бинарными отношениями
- •Лекция 5 Свойства и виды бинарных отношений
- •1 Свойства бинарных отношений
- •2 Виды бинарных отношений
- •Модуль II Основы комбинаторики Лекция 6 Основные понятия комбинаторики
- •1 Правила суммы и произведения
- •2 Выборки
- •Лекция 7 Методы решения задач комбинаторики
- •1 Метод включений и исключений
- •2 Метод рекуррентных соотношений
- •Модуль II Элементы теории графов Лекция 6 основные понятия теории графов
- •1 Понятие графа
- •2 Виды графов
- •3 Матрица смежности, инцидентности
- •4 Изоморфизм графов
- •Лекция 9 Операции над графами
- •1 Подграфы
- •2 Операции над графами
- •Лекция 10 Пути и связность в неориентированных графах
- •1 Основные определения
- •2 Обходы в графе
- •Лекция 9 Пути и связность в ориентированных графах
- •1 Виды связности
- •2 Выделение компонент сильной связности
- •Алгоритм выделения компонент сильной связности
- •Лекция 10 Расстояния в графах
- •1 Основные определения
- •2 Нахождение расстояний в графе
- •Алгоритм Дейкстры
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
- •Лекция 11 Деревья
- •1 Основные свойства деревьев
- •2 Нахождение центров дерева
- •3 Покрывающие деревья (остовы)
- •Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
- •Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- •Лекция 12 Двудольные и планарные графы
- •1 Двудольные графы
- •2 Планарные графы
- •Лекция 13 Раскраски графов
- •1 Раскраски
- •2 Внешняя и внутренняя устойчивость. Покрытия
- •Лекция 14 Потоки в сетях
- •1 Постановка задачи нахождения максимального потока
- •2 Решение задачи
- •Заключение
- •Библиографический список
Лекция 14 Потоки в сетях
План лекции
Постановка задачи нахождения максимального потока
Решение задачи
Ключевые слова: поток, пропускная способность ребра, величина потока, увеличивающая цепь.
1 Постановка задачи нахождения максимального потока
Задача о потоке в сети формулируется следующим образом. Дан ориентированный граф, в дальнейшем называемый сетью, с одним источником s (вершиной без входящих ребер) и одним стоком t (вершиной без выходящих ребер). Каждому ребру (i, j) графа приписано положительное число c(i, j), называемое пропускной способностью ребра.
Поток
в
сети — это функция
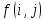 ,
определенная на ребрах графа и
удовлетворяющая следующим условиям:
,
определенная на ребрах графа и
удовлетворяющая следующим условиям:
1)
для любого графа 0 ≤
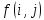 ≤c(i,
j);
≤c(i,
j);
2)
если
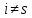 ,
,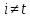 ,
то
,
то
 (закон
Кирхгофа);
(закон
Кирхгофа);
3)
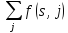 =
=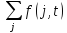 =v.
=v.
Число v называется величиной потока.
Задача
состоит в определении функции
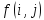 таким образом, чтобы величина потока
была максимальной.
таким образом, чтобы величина потока
была максимальной.
Введем
величину q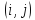 = c(i,j)
-
= c(i,j)
-
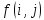 .
Обозначим черезQ
множество ребер, для
которых q(i,
j)
> 0, а через R
— множество ребер,
для которых
.
Обозначим черезQ
множество ребер, для
которых q(i,
j)
> 0, а через R
— множество ребер,
для которых
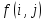 > 0. Эти множества могут пересекаться.
> 0. Эти множества могут пересекаться.
Цепь Р (без учета ориентации ребер) из s в t, все ребра которой, ориентированные от s к t (прямые), принадлежат Q, а все ребра, ориентированные от t к s (обратные), принадлежат R, называется увеличивающей. На рисунке 32 ребра (s, а), (а, b), (d, t) — прямые, а ребра (с, b), (d, с) — обратные.
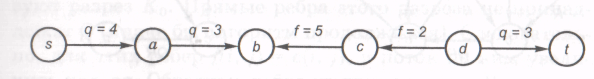
Рисунок 32 – Увеличивающая цепь
Если в сети с заданным потоком существует увеличивающая цепь, то величину потока в сети можно увеличить, изменяя величины потока на ребрах этой цепи. Рассмотрим, как это сделать.
2 Решение задачи
Первое (выходящее из s) и последнее (входящее в t) ребра увеличивающей цепи - всегда прямые. Любую неконцевую вершину j этой цепи можно отнести к одному из трех классов.
1. Входящее в нее ребро (i, j) и выходящее ребро (j, k) — прямые. На этих ребрах поток можно увеличить на одно и то же число, но не более, чем на величину min{q(i, j), q(j, k)} — при этом закон Кирхгофа в вершине j не будет нарушен. На рисунке 32 к этому классу относится вершина а.
2.
Входящее
в нее (со стороны s)
ребро (j,
i)
и выходящее (в сторону t)
ребро
(k,
у)
— обратные. На этих ребрах поток можно
уменьшить на одно и то же число, но не
более, чем на величину min{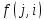 ,
,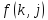 }
— при этом закон Кирхгофа также не будет
нарушен. На рисунке 32 к этому классу
относится вершинас,
для
которой входящим ребром считаем (с,
b),
а
выходящим — (d,
с).
}
— при этом закон Кирхгофа также не будет
нарушен. На рисунке 32 к этому классу
относится вершинас,
для
которой входящим ребром считаем (с,
b),
а
выходящим — (d,
с).
3.
Входящее
ребро (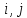 )
— прямое, а выходящее ребро(k,
j)
—
обратное, либо наоборот: входящее —
обратное, а выходящее — прямое. В обоих
случаях можно на прямом ребре поток
увеличить, а на обратном — уменьшить
на одну и ту же величину, не превосходящую
)
— прямое, а выходящее ребро(k,
j)
—
обратное, либо наоборот: входящее —
обратное, а выходящее — прямое. В обоих
случаях можно на прямом ребре поток
увеличить, а на обратном — уменьшить
на одну и ту же величину, не превосходящую
min{g(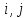 ),f(k,
j)}.
),f(k,
j)}.
На рисунке 32 к этому классу относятся вершины b (первый случай) и d (второй случай).
На
всех прямых ребрах увеличивающей цепи
увеличим поток на величину min{min{g(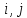 )},min{
)},min{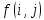 }},
а на всех
обратных ребрах — уменьшим его на ту
же величину. Тогда, поскольку первое и
последнее ребра цепи — прямые, на эту
величину возрастет и общая величина
потока. Таким образом, поток в сети можно
увеличивать до тех пор, пока в сети есть
увеличивающие цепи.
}},
а на всех
обратных ребрах — уменьшим его на ту
же величину. Тогда, поскольку первое и
последнее ребра цепи — прямые, на эту
величину возрастет и общая величина
потока. Таким образом, поток в сети можно
увеличивать до тех пор, пока в сети есть
увеличивающие цепи.
В
нашем примере min{min{
g(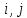 )},min{
)},min{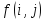 }}
= 2.
}}
= 2.
Схема алгоритма поиска увеличивающей цепи.
1. Пометить s.
2.
Для помеченной вершины
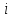 найти
смежную с ней непомеченную вершину
найти
смежную с ней непомеченную вершину
 ,
содержащуюся либо вQ,
либо
в R:
а)
если (
,
содержащуюся либо вQ,
либо
в R:
а)
если (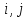 )
) Q,
пометить
Q,
пометить
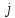 и (
и (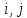 );
б) если (
);
б) если (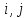 )
)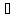 R,
пометить
R,
пометить
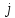 и (
и (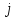 ,
,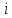 ).
).
3. Остановиться, если либо помечена t, либо шаг 2 невозможен. Иначе перейти к шагу 2.
Помеченные вершины и ребра образуют дерево, поскольку ребра, соединяющие две помеченные вершины, не рассматриваются. Поэтому, если t помечена, то тем самым построена единственная помеченная цепь из s в t, которая является увеличивающей. Если же шаг 3 невозможен, a t не помечена, то увеличивающих цепей нет.
Описанная
схема становится конкретным алгоритмом,
если зафиксировать правила выбора
помеченной вершины
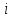 и
непомеченной вершины
и
непомеченной вершины
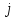 (в случае, когда дляi
имеется
несколько вершин
(в случае, когда дляi
имеется
несколько вершин
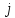 ,
удовлетворяющих условиям п. 2). Построенное
дерево зависит от выбора этого правила.
,
удовлетворяющих условиям п. 2). Построенное
дерево зависит от выбора этого правила.
Таким образом, общий алгоритм нахождения максимального потока формулируется следующим образом.
1. Определить начальный поток (например, нулевой).
2. Определить множества Q, R.
3. Найти увеличивающую цепь и провести на ней максимальное увеличение потока. Если такой цепи нет, закончить алгоритм. Иначе перейти к шагу 2.
На
рисунке 33 приведен пример построения
максимального потока, которое заканчивается
за три цикла. Вершины обозначены буквами,
пропускные способности — прямыми
жирными цифрами, поток на ребрах —
курсивными нежирными цифрами. Отсутствие
потока на ребре означает, что он равен
нулю.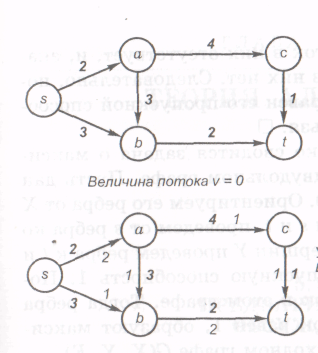
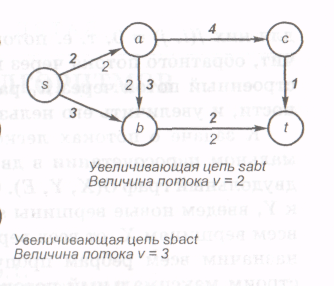
Рисунок 33 – Пример построения максимального потока
Теорема. Поток, построенный описанным алгоритмом, максимален.
Введем понятие разреза. Разрезом связного графа называется множество ребер, удаление которых делает граф несвязным. Весь поток в сети должен проходить через все разрезы. Пропускная способность разреза К равна
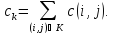
Поэтому
max
v
=
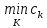 .Алгоритм
построения потока завершается, когда
больше нет увеличивающих цепей. Рассмотрим
неориентированное дерево, построенное
на последнем шаге алгоритма поиска
увеличивающей цепи, и выделим ребра,
соединяющие его помеченные ребра с
непомеченными. Эти ребра образуют разрез
К0.
Прямые
ребра этого разреза не принадлежат Q
(иначе бы алгоритм продолжился).
Следовательно, для этих ребер f(i,
j)
= c(i,
j),
и поток по ним увеличить нельзя. Обратные
ребра не принадлежат R,
поэтому
для них
.Алгоритм
построения потока завершается, когда
больше нет увеличивающих цепей. Рассмотрим
неориентированное дерево, построенное
на последнем шаге алгоритма поиска
увеличивающей цепи, и выделим ребра,
соединяющие его помеченные ребра с
непомеченными. Эти ребра образуют разрез
К0.
Прямые
ребра этого разреза не принадлежат Q
(иначе бы алгоритм продолжился).
Следовательно, для этих ребер f(i,
j)
= c(i,
j),
и поток по ним увеличить нельзя. Обратные
ребра не принадлежат R,
поэтому
для них
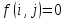 ,
т.е. поток в них отсутствует, и, значит,
обратного потока через них нет.
Следовательно, построенный поток черезК0.
равен его пропускной способности. и
увеличить его нельзя.
,
т.е. поток в них отсутствует, и, значит,
обратного потока через них нет.
Следовательно, построенный поток черезК0.
равен его пропускной способности. и
увеличить его нельзя.
