Лекция 9 Пути и связность в ориентированных графах

План лекции

1. Виды связности

2. Выделение компонент сильной связности

Ключевые слова: сильно связный, односторонне связный слабо связный орграф, несвязный орграф, сильно связанная компонента, матрица достижимости, матрица сильной связности.

1 Виды связности

Последовательность v₁x₁v₂x₂v₃…x_kv_k+1, (где k1, v_iV, i=1,…,k+1, x_iX, j=1,…,k), в которой чередуются вершины и дуги и для каждого j=1,…,k дуга x_j имеет вид (v_j,v_j+1), называется путем из v₁ в v_k+1.

Цепь – незамкнутый путь, в котором все дуги попарно различны.

Контур – замкнутый путь.

Простой путь – путь (контур), в котором ни одна дуга не встречается дважды.

Простой контур – контур, в котором все вершины попарно различны.

Гамильтонов путь (контур) – простой путь (контур), проходящий через все вершины.

Эйлеров путь ( контур) – путь (контур), содержащий все дуги графа по одному разу.

Длина пути – число дуг в пути.

Говорят, что вершина w ориентированного графа D достижима из вершины v, если либо w=v, либо существует путь из v в w.

Полупуть в ориентированном графе — это последовательность дуг, такая, что любые две соседних дуги различны и имеют общую инцидентную им вершину.

Иначе говоря, полупуть — это путь, который проходится без учета ориентации ребер.

Ориентированный граф называется сильно связным, если любые две вершины достижимы друг из друга.

Орграф называется односторонне связным, если для любой пары вершин существует путь между ними хотя бы в одну сторону.

Орграф называется слабо связным, если между любой парой вершин существует полупуть.

Орграф называется несвязным, если между некоторой парой вершин нет полупути.

Компонентой сильной связности ориентированного графа D называется его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа ориентированного графа D.

2 Выделение компонент сильной связности

Обозначим через A^k=[a^(k)_ij] k-ю степень матрицы смежности A(D).

Элемент a^(k)_ij матрицы A^k ориентированного псевдографа D=(V,X) равен числу всех путей длины k из v_i в v_j.

Матрица достижимости ориентированного графа D – квадратная матрица T(D)=[t_ij] порядка n, элементы которой равны

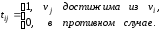
Матрица сильной связности ориентированного графа D – квадратная матрица S(D)=[s_ij] порядка n, элементы которой равны

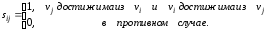
Матрица связности графа G – квадратная матрица S(G)=[s_ij] порядка n, элементы которой равны

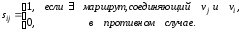
Пусть D=(V,X) – ориентированный граф, V={v₁,…, v_n}, A(D) – его матрица смежности. Тогда

1. T(D)=sgn[E+A+A²+A³+… A^n-1],

2. S(D)=T(D)T^T(D) (T^T-транспонированная матрица, - поэлементное умножение).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа, затем – матрицу сильной связностиS(D) ориентированного графа (она должна быть симметрической).

Алгоритм выделения компонент сильной связности

1. Присваиваем p=1 (p – количество компонент связности),.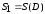

2. Включаем в множество вершин V_p компоненты сильной связности D_p вершины, соответствующие единицам первой строки матрицы S_p. В качестве матрицы A(D_p) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V_p.

3. Вычеркиваем из S_p строки и столбцы, соответствующие вершинам из V_p. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как S_p+1, присваиваем p=p+1 и переходим к п. 2.