
- •Лесосибирск 2012
- •Лекция 1 Основные понятия теории множеств
- •1 Понятие множества
- •2 Способы задания множеств
- •3 Сравнение множеств
- •Лекция 2 Операции над множествами
- •1 Операции над множествами
- •2 Свойства операций над множествами
- •Лекция 3 Соответствия и функции
- •1 Соответствия
- •2 Функции
- •Лекция 4 Бинарные отношения и операции над ними
- •1 Понятие бинарного отношения
- •2 Операции над бинарными отношениями
- •Лекция 5 Свойства и виды бинарных отношений
- •1 Свойства бинарных отношений
- •2 Виды бинарных отношений
- •Модуль II Основы комбинаторики Лекция 6 Основные понятия комбинаторики
- •1 Правила суммы и произведения
- •2 Выборки
- •Лекция 7 Методы решения задач комбинаторики
- •1 Метод включений и исключений
- •2 Метод рекуррентных соотношений
- •Модуль II Элементы теории графов Лекция 6 основные понятия теории графов
- •1 Понятие графа
- •2 Виды графов
- •3 Матрица смежности, инцидентности
- •4 Изоморфизм графов
- •Лекция 9 Операции над графами
- •1 Подграфы
- •2 Операции над графами
- •Лекция 10 Пути и связность в неориентированных графах
- •1 Основные определения
- •2 Обходы в графе
- •Лекция 9 Пути и связность в ориентированных графах
- •1 Виды связности
- •2 Выделение компонент сильной связности
- •Алгоритм выделения компонент сильной связности
- •Лекция 10 Расстояния в графах
- •1 Основные определения
- •2 Нахождение расстояний в графе
- •Алгоритм Дейкстры
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
- •Лекция 11 Деревья
- •1 Основные свойства деревьев
- •2 Нахождение центров дерева
- •3 Покрывающие деревья (остовы)
- •Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
- •Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- •Лекция 12 Двудольные и планарные графы
- •1 Двудольные графы
- •2 Планарные графы
- •Лекция 13 Раскраски графов
- •1 Раскраски
- •2 Внешняя и внутренняя устойчивость. Покрытия
- •Лекция 14 Потоки в сетях
- •1 Постановка задачи нахождения максимального потока
- •2 Решение задачи
- •Заключение
- •Библиографический список
Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
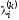 записываем в виде матрицы,i-
строка,k-столбец.
записываем в виде матрицы,i-
строка,k-столбец.
Составляем таблицу
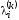 ,i=1,…,n,k=0,…,n-1.
Если
,i=1,…,n,k=0,…,n-1.
Если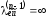 ,
то пути изvначвvконнет.
Конец алгоритма.
,
то пути изvначвvконнет.
Конец алгоритма.Если
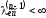 то это число выражает длину любого
минимального пути изvначвvкон.Найдем минимальноеk11,
при котором
то это число выражает длину любого
минимального пути изvначвvкон.Найдем минимальноеk11,
при котором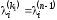 .
По определению
.
По определению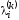 получим, чтоk1-
минимальное число дуг в пути среди всех
минимальных путей изvнач
вvкон.
получим, чтоk1-
минимальное число дуг в пути среди всех
минимальных путей изvнач
вvкон.Затем определяем номера i2,…,
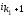 такие, что
такие, что
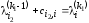 ,
,
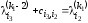 ,
,
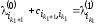 ,
,
то есть, восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из vначвvкон.
Лекция 11 Деревья
План лекции
Основные свойства деревьев
Нахождение центров дерева
Покрывающие деревья (остовы)
Ключевые слова: дерево, поддерево, лес, остовное дерево, цикломатическое число, хорда остова.
1 Основные свойства деревьев
Связный граф, не имеющий циклов, называется деревом. Связный подграф дерева называетсяподдеревом. Граф, у которого все связные компоненты являются деревьями, называетсялесом.
Каждый из изображенных на рисунке 23 графов является деревом. а их объединение – лесом.
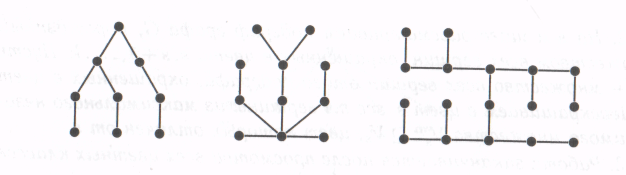
Рисунок 23 - Лес
Ориентированным деревом называется связный граф, не содержащий циклов, в котором только одна вершина, называемая корнем, не имеет входящих дуг, а все остальные вершины имеют по одной входящей дуге.
Свойства деревьев
В дереве любая цепь является простой.
Граф G1, полученный добавлением к дереву G новой вершины и ребра, связывающего эту вершину с одной из вершин графа G, является деревом.
Граф G является деревом тогда и только тогда, когда он не содержит циклов, но при добавлении любого ребра из него получается граф, содержащий ровно один простой цикл.
Если у дерева есть ребро, то у него есть висячая вершина.
Граф G является деревом тогда и только тогда, когда он связный и число его ребер на единицу меньше числа вершин.
В неориентированном дереве имеются по крайней мере две концевые вершины.
Между любыми двумя вершинами дерева имеется ровно один путь.
Дерево с п вершинами имеет п-1 ребро.
2 Нахождение центров дерева
Для неориентированных деревьев центры можно найти с помощью следующего алгоритма.
1. Обозначим исходное дерево G через G(1) и присвоим его концевым вершинам тип 1.
2. Если в полученном на предыдущем шаге графе G(i)(i = 1, 2, ...) все вершины — концевые, алгоритм заканчивается. В остальных случаях переходим к шагу 3.
3. Удалим в G(i) все концевые вершины вместе с инцидентными им ребрами. Полученный граф обозначим через G(i+1). Этот граф является деревом, поскольку удаленные ребра не входят ни в какой путь, соединяющий оставшиеся вершины, и, следовательно, их удаление не нарушает связности G(i+1). Концевым вершинам G(i+1) присвоим тип i + 1. Полагаем i = i + 1 и переходим к шагу 2.
В результате работы алгоритма каждой вершине исходного дерева присваивается тип. На каждом шаге номер типа увеличивается на единицу, и вершины, оставшиеся к последнему шагу, получают максимальный тип k.
Теорема. Центрами дерева являются вершины максимального типа k. Дерево имеет либо один, либо два центра, причем в первом случае радиус дерева равен k - 1, а во втором — k.
