Лекция 13 Раскраски графов

План лекции

1. Раскраски

2. Внешняя и внутренняя устойчивость. Покрытия.

Ключевые слова: раскраска,k-раскраска,k-раскрашиваемый граф, хроматическое число, внутренне устойчивое множество вершин, полностью зависимое множество, внешне устойчивое множество вершин, вершинное покрытие.

1 Раскраски

Раскраска элементов графа в k цветов, или k-раскраска — это разбиение элементов графа на k классов. Рассматривают раскраски вершин и ребер неориентированных графов, а также раскраски граней плоских карт. Раскраска называется правильной, если любая пара смежных элементов окрашена в разные цвета. (Грани плоской карты считаются смежными, если их границы имеют хотя бы одно общее ребро.) Задача раскраски заключается в нахождении минимального числа цветов, достаточного для правильной раскраски.

Задача о раскраске плоских карт — одна из самых старых проблем теории графов. Еще в конце XIX в. было доказано, что для раскраски любой плоской карты достаточно пяти красок. Высказанная тогда же «гипотеза четырех красок» (всегда достаточно четырех красок) была доказана в 70-х гг. XX в. американскими математиками Аппелем и Хакеном. Их существенно использовало компьютерные вычисления, поскольку было связано с построением и анализом около двух тысяч различных случаев.

В дальнейшем мы ограничимся сведениями о вершинных раскрасках.

Граф называется k-раскрашиваемым, если существует его правильная вершинная k-раскраска.

Хроматическим числом χ(G) графа G называется минимальное число k, для которого граф G k -раскрашиваемый. Граф G называется k -хроматическим, если χ(G) = k, и бихроматическим, если χ(G) = 2.

Пример. Граф на рисунке 30 — 3-хроматический.

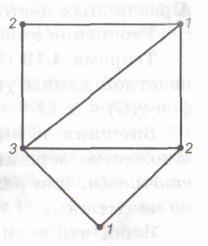
Рисунок 30 - 3-хроматический граф

Теорема. Граф является бихроматическим, если и только если он двудольный.

Следствие. Всякое дерево является двудольным графом.

Обозначим через Δ максимальную из степеней вершин в графе.

Теорема. Для любого простого графа χ(G) ≤ Δ + 1. Это означает, что любой простой граф можно раскрасить в Δ + 1 цветов.

Метод такой раскраски заключается в следующем. Пусть дано множество Δ + 1 цветов. Первой выбранной вершине присваиваем произвольный цвет из этого множества. В дальнейшем каждой выбираемой вершине v присваиваем цвет, который не присвоен смежным с ней вершинам. Это всегда возможно, так как d(v) ≤ Δ, и, следовательно, вершинам, смежным с v, присвоено не более Δ различных цветов.

Уточнение этой оценки дает теорема Брукса.

Теорема (Брукс). Для полных графов и циклов нечетной длины χ(G) = Δ + 1. Для всех остальных графов χ(G) ≤ Δ.

2 Внешняя и внутренняя устойчивость. Покрытия

Множество вершин графа G называется внутренне устойчивым, или независимым, если его вершины попарно не смежны.

Ясно, что если множество М внутренне устойчиво, то и любое его подмножество также внутренне устойчиво. С другой стороны, множество всех вершин любого непустого графа внутренне устойчивым не является. Поэтому множество всех внутренне устойчивых множеств частично упорядочено по включению, и существуют максимальные внутренне устойчивые множества, т. е. такие, добавление к которым любой вершины нарушает внутреннюю устойчивость.

Наибольшая из мощностей максимальных внутренне устойчивых множеств графа G называется числом внутренней устойчивости и обо­значается α₀(G).

Пример. В графе на рисунке 31 внутренне устойчивое множество {а, с} максимально по включению, но не наибольшее по мощности. Наибольшим является множество {b, d, f}; α (G) = 3.

Множество называется полностью зависимым, если все его вершины попарно смежны.

Множество X вершин графа G называется внешне устойчивым, если любая вершина G смежна с некоторой вершиной из X. Множество X вершин графа G называется вершинным покрытием, если оно покрывает все ребра, т. е. любое ребро G инцидентно некоторой вершине из X.

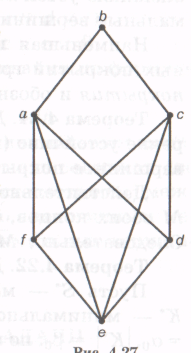
Рисунок 31 –Граф

Пример. Множество {а, с} на рисунке 31 внешне устойчиво, но не является вершинным покрытием, так как не покрывает ребра (е, f) и (d,е).

Очевидно, что если множество М внешне устойчиво, то и любое множество вершин, содержащее X, также внешне устойчиво. Поэтому множество всех внешне устойчивых множеств частично упорядочено по включению, и существуют минимальные внешне устойчивые множества, т. е. такие, удаление из которых любой вершины нарушает внешнюю устойчивость. Аналогично, существуют минимальные вершинные покрытия.

Наименьшая из мощностей минимальных вершинных покрытий графа G называется числом вершинного покрытия и обозначается βo(G).

Теорема. Для простого графа G=(V, Е) М 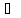V внутренне устойчиво (независимо), если и только если М — вершинное покрытие.

Действительно, так как ни одно ребро не содержит в М обоих концов, то концы всех ребер содержатся в М. Следовательно, М -- вершинное покрытие. D

Теорема 4.22. Для простого графа G=(V, Е) α ₀ + β₀ = п.