
- •Лесосибирск 2012
- •Лекция 1 Основные понятия теории множеств
- •1 Понятие множества
- •2 Способы задания множеств
- •3 Сравнение множеств
- •Лекция 2 Операции над множествами
- •1 Операции над множествами
- •2 Свойства операций над множествами
- •Лекция 3 Соответствия и функции
- •1 Соответствия
- •2 Функции
- •Лекция 4 Бинарные отношения и операции над ними
- •1 Понятие бинарного отношения
- •2 Операции над бинарными отношениями
- •Лекция 5 Свойства и виды бинарных отношений
- •1 Свойства бинарных отношений
- •2 Виды бинарных отношений
- •Модуль II Основы комбинаторики Лекция 6 Основные понятия комбинаторики
- •1 Правила суммы и произведения
- •2 Выборки
- •Лекция 7 Методы решения задач комбинаторики
- •1 Метод включений и исключений
- •2 Метод рекуррентных соотношений
- •Модуль II Элементы теории графов Лекция 6 основные понятия теории графов
- •1 Понятие графа
- •2 Виды графов
- •3 Матрица смежности, инцидентности
- •4 Изоморфизм графов
- •Лекция 9 Операции над графами
- •1 Подграфы
- •2 Операции над графами
- •Лекция 10 Пути и связность в неориентированных графах
- •1 Основные определения
- •2 Обходы в графе
- •Лекция 9 Пути и связность в ориентированных графах
- •1 Виды связности
- •2 Выделение компонент сильной связности
- •Алгоритм выделения компонент сильной связности
- •Лекция 10 Расстояния в графах
- •1 Основные определения
- •2 Нахождение расстояний в графе
- •Алгоритм Дейкстры
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
- •Лекция 11 Деревья
- •1 Основные свойства деревьев
- •2 Нахождение центров дерева
- •3 Покрывающие деревья (остовы)
- •Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
- •Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- •Лекция 12 Двудольные и планарные графы
- •1 Двудольные графы
- •2 Планарные графы
- •Лекция 13 Раскраски графов
- •1 Раскраски
- •2 Внешняя и внутренняя устойчивость. Покрытия
- •Лекция 14 Потоки в сетях
- •1 Постановка задачи нахождения максимального потока
- •2 Решение задачи
- •Заключение
- •Библиографический список
Лекция 4 Бинарные отношения и операции над ними
План лекции
Понятие бинарного отношения
Операции над бинарными отношениями
Ключевые слова: бинарное отношение, пересечение, объединение, произведение бинарных отношений.
1 Понятие бинарного отношения
В математике для обозначения связи между предметами или понятиями используют термин «отношение». Например, отношение «меньше» в множестве действительных чисел, отношение подобия треугольников, отношения родства и старшинства в множестве людей и др. Это примеры отношений между двумя элементами (понятиями) так называемых бинарных отношений.
Определение. Бинарным отношением, определенным на паре множеств А и В, называется любое подмножество их декартова произведения А × В.
Если
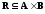 — бинарное
отношение, а упорядоченная пара (а,
b),
где
— бинарное
отношение, а упорядоченная пара (а,
b),
где
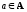 ,
,
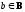 ,принадлежит
R, то это
записывают либо
,принадлежит
R, то это
записывают либо
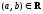 (согласно определению), либоR(а,
b),
либо aRb.
Обозначение aRb
исходит из обозначений вида а
= b,
а
< b,
(согласно определению), либоR(а,
b),
либо aRb.
Обозначение aRb
исходит из обозначений вида а
= b,
а
< b,
 и др.
и др.
Если
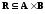 — бинарное
отношение и
А = В,
то R
называют бинарным
отношением, определенным на множестве
А.
— бинарное
отношение и
А = В,
то R
называют бинарным
отношением, определенным на множестве
А.
Два
бинарных отношения
R1
и R2
равны тогда и только тогда, когда любая
пара (а,
b)
из R1
принадлежит вместе с тем и
R2,
и обратно:
любая пара (а,
b)
из R2
принадлежит и
R1.
Аналогично,
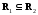 тогда и только тогда, когда любая пара
(а,
b)
из R1
принадлежит вместе с тем и
R2.
тогда и только тогда, когда любая пара
(а,
b)
из R1
принадлежит вместе с тем и
R2.
Определение.
Пусть
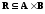 — бинарное
отношение, определенное на паре множеств
А,
В.
Областью
определения отношения
R
называется совокупность всех таких
— бинарное
отношение, определенное на паре множеств
А,
В.
Областью
определения отношения
R
называется совокупность всех таких
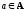 ,
что
,
что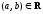 хотя бы для одного
хотя бы для одного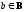 .Областью
значений отношения
R
называют множество всех таких
.Областью
значений отношения
R
называют множество всех таких
 ,
что
,
что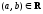 хотя бы для одного элемента
хотя бы для одного элемента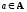 .
.
Пусть
А — произвольное
множество. Множество
А×A
называют
универсальным
отношением,
определенным на множестве
А; любая пара
(a1,
a2),
где
 ,
находится в этом отношении, поэтому его
называют иногдавсюду
истинным отношением.
Пустое подмножество множества А2
называют пустым
отношением;
ни одна из пар множества А2
не находится в этом отношении, поэтому
оно называется еще всюду
ложным отношением.
Отношение равенства, определенное на
множестве
А, совпадает
с множеством так называемых диагональных
пар: (а,
а),
где
,
находится в этом отношении, поэтому его
называют иногдавсюду
истинным отношением.
Пустое подмножество множества А2
называют пустым
отношением;
ни одна из пар множества А2
не находится в этом отношении, поэтому
оно называется еще всюду
ложным отношением.
Отношение равенства, определенное на
множестве
А, совпадает
с множеством так называемых диагональных
пар: (а,
а),
где
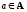 ,
и обозначаетсяеA
или просто е,
если ясно, какое множество
А рассматривается.
,
и обозначаетсяеA
или просто е,
если ясно, какое множество
А рассматривается.
По аналогии с понятием бинарного отношения вводится и понятие n-арного (n-местного) отношения.
Определение. Пусть A1, …, An — непустые множества. Всякое подмножество R их декартового произведения А1×An называется отношением, определенным на системе множеств A1, …, An.
Если A1 = … = An = А, то отношение R, определенное на системе множеств A1, …, An, называют n-арным (n-местным) отношением, определенным на множестве А.
2 Операции над бинарными отношениями
Так
как бинарные отношения, определенные
на фиксированной паре множеств
А, В,
являются подмножествами А×В,
то над ними можно производить операции
объединения, пересечения и дополнения
(в множестве А×В).
Так, если R,
S
— два бинарных отношения, определенных
па паре множеств А,
В, то для
любых
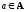 ,
,
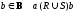 тогда и только тогда, когда aRb
или aSb;
тогда и только тогда, когда aRb
или aSb;
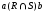 тогда и только тогда, когдаaRb
и aSb;
тогда и только тогда, когдаaRb
и aSb;
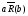 тогда и только тогда, когда неaRb.
тогда и только тогда, когда неaRb.
Помимо теоретико-множественных операций над отношениями важное значение имеют еще две операции над ними: обращение и умножение отношений.
Определение.
Пусть
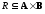 — бинарное
отношение, определенное на паре множеств
А,
В.
Отношением,
обратным к бинарному отношению R,
называется отношение, определенное на
паре множеств
В и
А и состоящее
из всех тех и только тех пар (b,
а),
для которых
— бинарное
отношение, определенное на паре множеств
А,
В.
Отношением,
обратным к бинарному отношению R,
называется отношение, определенное на
паре множеств
В и
А и состоящее
из всех тех и только тех пар (b,
а),
для которых
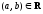 (
(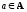 ,
,
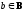 ).
).
Бинарное
отношение, обратное к отношению R,
обозначается R–1.
Таким образом,
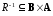 .
.
Если R — бинарное отношение «х является родителем у», то R–1 — отношение «х является ребенком (сыном или дочерью) у».
Определение.
Пусть
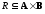 — бинарное
отношение, определенное на паре множеств
А,
В, а
— бинарное
отношение, определенное на паре множеств
А,
В, а
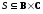 — бинарное отношение, определенное на
паре множеств
В, С.
Произведением
отношений R
и S
называется
бинарное отношение, определенное на
паре множеств
А и С
и состоящее из всех тех и только тех пар
(а,
с)
(
— бинарное отношение, определенное на
паре множеств
В, С.
Произведением
отношений R
и S
называется
бинарное отношение, определенное на
паре множеств
А и С
и состоящее из всех тех и только тех пар
(а,
с)
(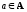 ,
,
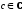 ),
для которых существует элемент х
из
В такой, что
aRx
и xSc.
),
для которых существует элемент х
из
В такой, что
aRx
и xSc.
Произведение
бинарных отношений
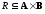 и
и
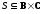 обозначим черезRS.
Таким образом,
обозначим черезRS.
Таким образом,
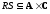 иa(RS)c
тогда и только тогда, когда существует
элемент
иa(RS)c
тогда и только тогда, когда существует
элемент
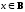 такой, что
aRx
и xSc.
такой, что
aRx
и xSc.
Теорема
1. Пусть
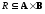 ,
,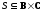 ,
,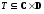 — бинарные отношения. Тогда произведения
(RS)T
и R(ST)
определены
и (RS)T
= R(ST).
То есть умножение бинарных отношений
ассоциативно.
— бинарные отношения. Тогда произведения
(RS)T
и R(ST)
определены
и (RS)T
= R(ST).
То есть умножение бинарных отношений
ассоциативно.
Теорема
2. Пусть
 ,
,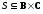 — бинарные отношения. Тогда выражения
(RS)–1
и S–1R–1
определены и имеет место равенство
(RS)–1
= S–1R–1.
— бинарные отношения. Тогда выражения
(RS)–1
и S–1R–1
определены и имеет место равенство
(RS)–1
= S–1R–1.
