Лекция 10 Расстояния в графах

План лекции

1. Основные определения

2. Нахождение расстояний в графе

Ключевые слова: расстояние между вершинами, радиус, диаметр. центр, графа, эксцентриситет вершины.

1 Основные определения

Расстоянием между вершинами 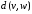называется минимальная длина пути между ними, при этом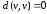,,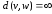 если не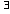пути.

Расстояние в графе удовлетворяют аксиомам метрики

1) ,

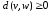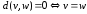
2) 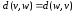(в неориентированном графе)

3)

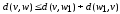
4) 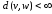в связном неориентированном графе.

Пусть 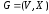связный граф (или псевдограф).

Диаметром графа G называется величина .

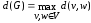Пусть .

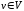Максимальным удалением (эксцентриситетом) в графе G от вершины 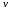называется величина.

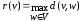Радиусом графа G называется величина

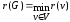
Центром графа G называется любая вершина 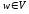такая, что.

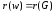Матрицей расстояний графа G с вершинами v₁,...,v_n называется квадратная матрица порядка п, в которой для 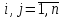элемент 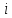-й строки и j-гo столбца равен расстоянию между вершинами v_i и v_j.

В прикладных задачах обычно рассматриваются помеченные графы, в которых ребрам приписаны некоторые действительные числа. Длины маршрутов в таких графах определяются не числом пройденных ребер, а суммой весов этих ребер. Всю информацию о взвешенном графе можно получить из матрицы весов.

Матрица весов графа (длин дуг орграфа) G квадратная, ее порядок совпадает с порядком графа (орграфа). Элемент, стоящий на пересече­нии i-й строки и j-гo столбца, равен весу ребра (дуги) (v_i, v_j), если такое ребро (такая дуга) существует, в противном случае он равен .

Весом (или длиной) маршрута во взвешенном графе называется сумма весов ребер, входящих в этот маршрут. Взвешенным расстоянием между вершинами u и v называется наименьший из весов маршрутов, связывающих u и v. Маршрут от u до v, вес которого совпадает со взвешенным расстоянием между u и v, называется кратчайшим (минимальным).

2 Нахождение расстояний в графе

Алгоритм Дейкстры позволяет найти взвешенные расстояния от какой-либо вершины v графа до остальных вершин в случае, когда веса всех ребер неотрицательны. Работа алгоритма происходит по шагам. На каждом шаге каждой вершине w приписываются метки, указывающие минимальный из весов изученных маршрутов, связывающих данную вершину с вершиной v и соседнюю с w вершину, через которую проходит наилучший маршрут. При поиске взвешенных расстояний в орграфе учитывается ориентация дуг.

Алгоритм Дейкстры

0. У каждой вершины ставим временную метку (0, ).

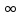1. У вершины v, от которой отсчитываются расстояния, метку (0,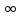)заменяем постоянной меткой (v, 0).

2. Ищем вершину, которая приобрела постоянную метку по­следней. Пусть и — такая вершина, и ее постоянная метка равна (х_u,у_u). Предположим, что вершина р является концом дуги, выходящей из и, имеет временную метку (х_р,у_р) и дуга (и,р) имеет вес h. Если метка вершины р имеет вид (0, 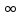)или отлична от (0, 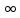), носумма у_и + h меньше у_р, то меняем метку (х_р,у_р) на (и,у_и + h). Так поступаем со всеми вершинами, имеющими временные метки и являющимися концом дуги с началом в и.

3. Среди вершин, имеющих временные метки, ищем ту, у которой число, стоящее в метке вторым, наименьшее. Делаем эту метку постоянной.

4. Если есть вершины с временными метками, переходим к п. 2.

5. Работа заканчивается, когда все вершины получат постоянные метки. Расстояние, указанное в метке, является взвешенным расстоянием от данной вершины до вершины v.

6. Постоянные метки позволяют найти кратчайший маршрут от вершины v до любой вершины и. От вершины и переходим к вершине u₁, указанной в метке вершины и. От вершины u₁ переходим к. вершине и₂, указанной в метке вершины u₁, и т. д. В некоторый момент мы попадем в вершину v. Теперь надо пройти все вершины в обратном порядке и получить требуемый маршрут.

Рассмотрим задачу нахождения минимального пути из вершины v_начвv_кон.

Пусть D=(V,X) – взвешенный ориентированный граф,V={v₁,…,v_n},n>1. Введем величины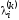, гдеi=1,…,n,k=0,1,2,…,n–1.

Для каждого фиксированного iиkвеличина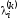равна длине минимального пути среди путей изv_начвv_iсодержащих не болееkдуг. Если путей нет, то.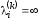

Положим также .

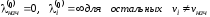Составляем матрицу длин дуг C(D)=[c_ij] порядкаn:

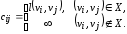
Утверждение. Приi=2,…,n,k0 выполняется равенство

.
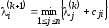