- •Лесосибирск 2012
- •Лекция 1 Основные понятия теории множеств
- •1 Понятие множества
- •2 Способы задания множеств
- •3 Сравнение множеств
- •Лекция 2 Операции над множествами
- •1 Операции над множествами
- •2 Свойства операций над множествами
- •Лекция 3 Соответствия и функции
- •1 Соответствия
- •2 Функции
- •Лекция 4 Бинарные отношения и операции над ними
- •1 Понятие бинарного отношения
- •2 Операции над бинарными отношениями
- •Лекция 5 Свойства и виды бинарных отношений
- •1 Свойства бинарных отношений
- •2 Виды бинарных отношений
- •Модуль II Основы комбинаторики Лекция 6 Основные понятия комбинаторики
- •1 Правила суммы и произведения
- •2 Выборки
- •Лекция 7 Методы решения задач комбинаторики
- •1 Метод включений и исключений
- •2 Метод рекуррентных соотношений
- •Модуль II Элементы теории графов Лекция 6 основные понятия теории графов
- •1 Понятие графа
- •2 Виды графов
- •3 Матрица смежности, инцидентности
- •4 Изоморфизм графов
- •Лекция 9 Операции над графами
- •1 Подграфы
- •2 Операции над графами
- •Лекция 10 Пути и связность в неориентированных графах
- •1 Основные определения
- •2 Обходы в графе
- •Лекция 9 Пути и связность в ориентированных графах
- •1 Виды связности
- •2 Выделение компонент сильной связности
- •Алгоритм выделения компонент сильной связности
- •Лекция 10 Расстояния в графах
- •1 Основные определения
- •2 Нахождение расстояний в графе
- •Алгоритм Дейкстры
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из vнач в vкон.( vнач ≠ vкон)
- •Лекция 11 Деревья
- •1 Основные свойства деревьев
- •2 Нахождение центров дерева
- •3 Покрывающие деревья (остовы)
- •Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
- •Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- •Лекция 12 Двудольные и планарные графы
- •1 Двудольные графы
- •2 Планарные графы
- •Лекция 13 Раскраски графов
- •1 Раскраски
- •2 Внешняя и внутренняя устойчивость. Покрытия
- •Лекция 14 Потоки в сетях
- •1 Постановка задачи нахождения максимального потока
- •2 Решение задачи
- •Заключение
- •Библиографический список
3 Сравнение множеств
Иногда
приходится рассматривать и множество,
не содержащее ни одного элемента. Оно
называется пустым
и обозначается
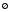 .
При задании множества характеристическим
свойством не всегда известно, существует
ли элемент с таким свойством. Например,
мы говорим о множестве решений какого-либо
уравнения, которое может и не иметь
решения, т.е. это множество решений
уравнения пустое.
.
При задании множества характеристическим
свойством не всегда известно, существует
ли элемент с таким свойством. Например,
мы говорим о множестве решений какого-либо
уравнения, которое может и не иметь
решения, т.е. это множество решений
уравнения пустое.
Определение.
Пусть А и
В — непустые
множества. Если каждый элемент множества
А является
вместе с тем и элементом множества
В, то
А называют
подмножеством
множества
В (или
А содержится
в В, или
В содержит
А, или
А включено
в В)
и обозначают
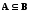 .
Положим, по определению, что пустое
множество
.
Положим, по определению, что пустое
множество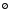 есть подмножество любого множестваВ,
в том числе и пустого.
есть подмножество любого множестваВ,
в том числе и пустого.
Пусть,
например, С
— множество всех комплексных чисел; R
— множество всех действительных чисел;
Q
— множество всех рациональных чисел;
Z
— множество всех целых чисел; N
— множество всех натуральных чисел.
Тогда
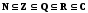 .
.
Понятие подмножества определяет отношение между двумя множествами — отношение включения. Отметим простейшие свойства введенного отношения включения:
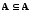 ,
т. е. любое множество
А является
подмножеством самого себя (рефлексивность);
,
т. е. любое множество
А является
подмножеством самого себя (рефлексивность);если
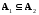 ,
,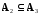 ,
то
,
то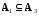 (транзитивность).
(транзитивность).
Чтобы
в множестве
А выделить
подмножество
В, добавляют
к характеристическому признаку множества
А то или иное
дополнительное свойство Р(х)
и обозначают это так: B
= { |P(x)}.
Например, {
|P(x)}.
Например, {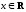 |x>0}
— множество
всех положительных действительных
чисел.
|x>0}
— множество
всех положительных действительных
чисел.
Введем наряду с отношением включения множеств еще одно отношение — отношение равенства множеств.
Определение.
Пусть А и
В — два
множества. Множества
А и
В называются
равными,
если каждый элемент множества
А является
вместе с тем и элементом множества
В, и обратно,
каждый элемент множества
В является
и элементом множества А.
Другими словами, множества
А и
В называются
равными, если выполняются два включения:
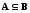 и
и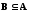 .
.
Отношение равенства двух множеств, очевидно, удовлетворяет следующим условиям:
А = А (рефлексивность);
если А = В и В = С, то А = С (транзитивность).
Если
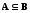 и
и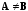 ,
тоА
называют собственным
подмножеством множества
В и обозначают
,
тоА
называют собственным
подмножеством множества
В и обозначают
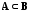 .
Введенное отношение
.
Введенное отношение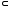 называетсяотношением
строгого включения.
Например,
называетсяотношением
строгого включения.
Например,
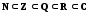 .
Отношение строгого включения удовлетворяет
следующему свойству: если
.
Отношение строгого включения удовлетворяет
следующему свойству: если
 и
и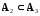 ,
то
,
то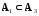 (транзитивность).
(транзитивность).
Лекция 2 Операции над множествами
План лекции
1. Операции над множествами
2. Свойства операций над множествами
Ключевые слова: объединение, пересечение, разность, декартово произведение множеств, дополнение множества
1 Операции над множествами
Во всех рассуждениях о нескольких множествах будем предполагать, что они являются подмножествами некоторого фиксированного множества, которое назовем универсальным или универсумом и будем обозначать E.
Определение.
Пересечением
множеств
А и
В называется
множество, обозначаемое
 и состоящее
из всех тех и только тех элементов,
которые принадлежат обоим множествам
А и В.
и состоящее
из всех тех и только тех элементов,
которые принадлежат обоим множествам
А и В.
Это
определение символически можно записать
так:
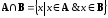 .
Например,
.
Например,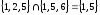 ;
;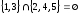 .
.
Определение.
Объединением
множеств
А и
В называется
множество, обозначаемое
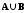 и состоящее
из всех тех и только тех элементов,
которые принадлежат хотя бы одному из
множеств А,
В.
и состоящее
из всех тех и только тех элементов,
которые принадлежат хотя бы одному из
множеств А,
В.
Это
определение символически можно записать
так:
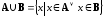 .
Например,
.
Например,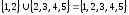 .
.
Отметим, что объединение множеств А и В называют иногда суммой и обозначают А+В, а их пересечение — произведением и обозначают АВ.
Определение. Разностью множеств А и В называют множество, обозначаемое А\В и состоящее из элементов, принадлежащих множеству А и не принадлежащих множеству В.
Определение.
Пусть А —
подмножество множества E.
Дополнением
множества
А в множестве
E
называют множество, состоящее из всех
тех и только тех элементов из
E,
которые не принадлежат А,
и обозначают
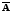 .
.
Например,
если E
— множество всех целых чисел,
А — множество
всех четных чисел, то
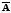 — множество
всех нечетных чисел.
— множество
всех нечетных чисел.
Операции объединения, пересечения, разности и дополнения множеств допускают наглядное графическое истолкование с помощью так называемых кругов Эйлера (или диаграмм Венна). Универсальное множество Е изображается при этом множеством точек некоторого прямоугольника, а его подмножества — в виде круга (или какой-нибудь другой простой области внутри этого прямоугольника).
Если
изобразить таким образом множества
А и
В, то множества
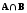 (рисунок 1),
(рисунок 1),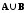 (рисунок 2) и
(рисунок 2) и
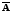 (рисунок 3)
изображаются заштрихованными областями.
(рисунок 3)
изображаются заштрихованными областями.
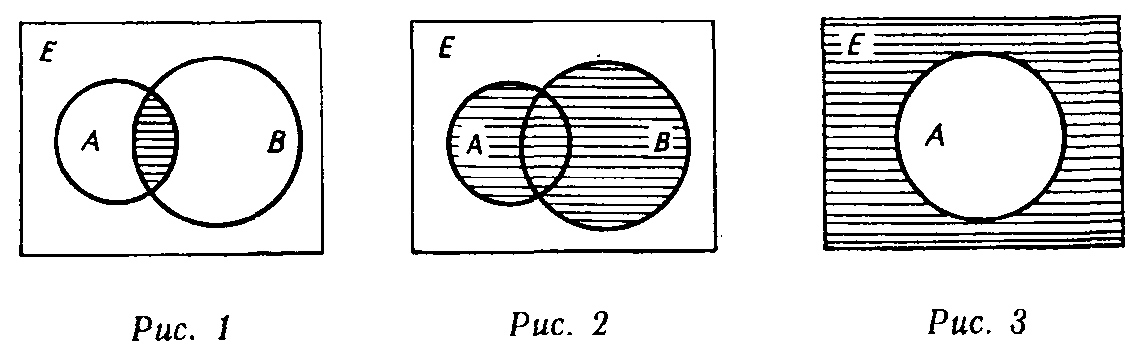
Рисунок
1 -
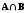 Рисунок 2 –
Рисунок 2 – Рисунок 3 -
Рисунок 3 -