2 Планарные графы

Граф укладывается на поверхности S, если его можно изобразить на этой поверхности так, что никакие два ребра не будут пересекаться.

Связный неориентированный граф называется планарным, если его можно уложить на плоскость, и плоским, если он уже уложен на плоскости.

Область плоскости, ограниченная простым циклом и не содержащая никакой другой цикл, называется внутренней гранью; единственная внешняя по отношению к графу область называется внешней гранью. Плоский граф со всеми его гранями называется плоской картой.

Плоская карта отличается от плоского графа тем, что она включает в себя внешнюю грань, т. е. образует полное разбиение плоскости; плоский же граф — это лишь часть плоскости.

На рисунке 25 показан планарный граф, изображенный так, что его ребра пересекаются, а на рисунке 26 тот же граф без пересечений ребер, т. е. плоский граф. Z₁, Z₂, Z ₃ — внутренние грани графа, Z₀ – внешняя грань.

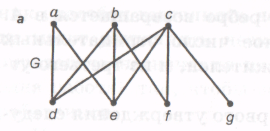
Рисунок 25 – Планарный граф

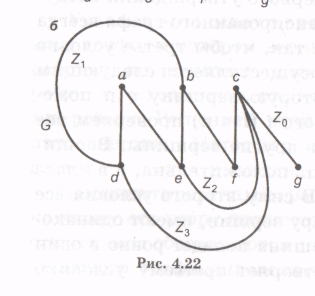
Рисунок 26 – Плоский граф

Не всякий граф является планарным. Стандартным примером непланарного графа является граф K_3,3 (рисунок 24), возникающий в известной задаче «о трех домах и трех колодцах», в которой жители домов хотели бы ходить за водой к любому колодцу так, чтобы их тропы не пересекались, т. е. чтобы никогда не встречать своих соседей. Для этого граф, соединяющий дома и колодцы, должен быть планарным. Однако он непланарен, так что эта задача не имеет решения. Другой важный пример непланарного графа — полный граф К₅ (рисунок 27).

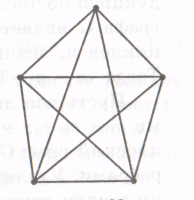
Рисунок 27 – Граф К₅

Теорема (Эйлер). Для плоской карты с п вершинами, т ребрами, r гранями

п - т + r = 2.

Следствие 1. Если G — плоская карта, в которой каждая грань содержит q ребер, то

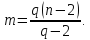
Максимальным планарным графом называется простой планарный граф, который при добавлении любого ребра (без добавления вершин) перестает быть либо простым, либо планарным. Легко видеть, что в максимальном планарном графе все грани ограничены циклами длины 3 (грани с такими границами будем называть треугольниками): внутри грани с более длинными границами всегда можно провести хотя бы одно ребро, а граница длины 2 – это пара кратных ребер, которых в простом графе нет.

Заметим, что если планарный граф содержит ребро, не принадлежащее никакому циклу и, следовательно, никакой границе, то он не является максимальным.

Следствие 2. Для максимального планарного графа т = Зп - 6.

Следствие 3. Если G — простой планарный граф с числом вершин п ≥ 3, то

т ≤ Зп - 6 (неравенство Эйлера).

Это следствие, во-первых, дает необходимое условие планарности, а во-вторых, показывает, что в простых планарных графах не может быть слишком много ребер: если для произвольного простого графа без петель т ≤ п(п - 1)/2, то для планарного графа т ≤ Зn - 6.

Теорема. В простом планарном графе с п вершинами, т ребрами и г гранями 3r ≤ 2т.

Следствие. Графы К₅ и К₃,₃ не являются планарными.

Необходимые и достаточные условия планарности содержит теорема Понтрягина-Куратовского, для формулировки которой введем некоторые понятия.

Слиянием, или стягиванием, двух ребер (и, v), (v, w), инцидентных вершине степени 2, называется операция, которая эти ребра заменяет одним ребром (и, w) и удаляет вершину v.

Разбиением ребра (и, w) называется операция, обратная слиянию, т. е. добавление новой вершины v степени 2 и замена ребра (и, w) парой ребер (и, v), (v, w).

Пример этих операций приведен на рисунке 28.

Рисунок 28 – Разбиение и стягивание ребра

Переход от графа G₁ к графу G₂ — это стягивание, а переход от графа G₂ к графу G₁ — разбиение.

Два графа называются гомеоморфными, если они изоморфны или могут быть сделаны изоморфными в результате конечного числа слияний и разбиений.

На рисунке 29 представлены два гомеоморфных графа.

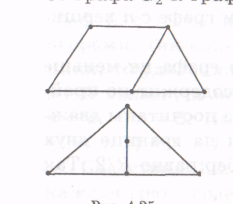
Рисунок 29 – Гомеоморфные графы

Теорема (Понтрягин, Куратовский). Граф планарен, если и только если он не содержит подграфов, гомеоморфных К₅ и К₃,₃.